Хорда на окружности выбранного диаметра
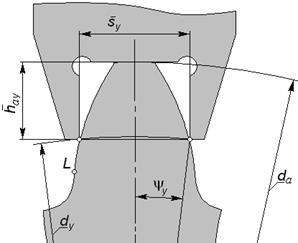 | 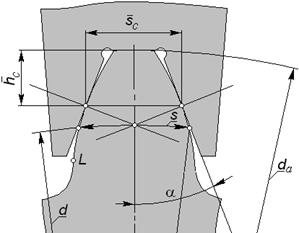 |
| Рис. 5.20 | Рис. 5.21 |
Схема измерения с помощью специального шаблона или зубомера показана на рис. 5.20; при этом контролируются два взаимосвязанных размера – 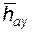 и
и 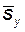 . Расчет этих размеров выполняют в следующем порядке:
. Расчет этих размеров выполняют в следующем порядке:
· выбирают диаметр 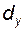 – любое значение в пределах
– любое значение в пределах 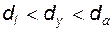 ; для неподрезанных зубьев диаметр
; для неподрезанных зубьев диаметр 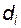 находят по формуле (5.19); если зубья подрезаны, то в (5.19) вместо
находят по формуле (5.19); если зубья подрезаны, то в (5.19) вместо 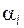 подставляют
подставляют 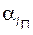 ; для выбранного значения диаметра
; для выбранного значения диаметра 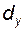 находят:
находят:
· угол профиля
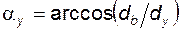 ; (5.74)
; (5.74)
· половину угловой толщины зуба на выбранной окружности
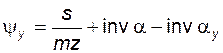 ; (5.75)
; (5.75)
если толщина зуба s не рассчитывалась, то величину 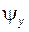 можно найти и по другой формуле
можно найти и по другой формуле
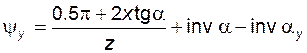 ; (5.76)
; (5.76)
· толщину зуба по хорде
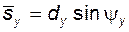 ; (5.77)
; (5.77)
· высоту зуба до хорды
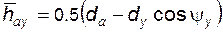 . (5.78)
. (5.78)
Иногда возникает необходимость по результатам измерения размеров 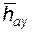 и
и 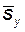 определить фактические значения s (или x); в этом случае находят фактические значения, соответствующие результатам измерений:
определить фактические значения s (или x); в этом случае находят фактические значения, соответствующие результатам измерений:
· диаметра окружности, проходящей через концы хорды 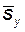
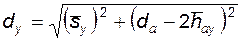 ; (5.79)
; (5.79)
· половины угловой толщины зуба на окружности диаметра 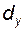
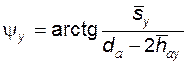 ; (5.80)
; (5.80)
· угла профиля 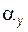 – по формуле (5.74);
– по формуле (5.74);
· делительной толщины зуба
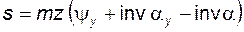 ; (5.81)
; (5.81)
· коэффициента смещения
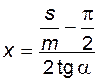 . (5.82)
. (5.82)
Описанный способ контроля достаточно прост, но ему свойственны такие недостатки:
а) кромки мерительного инструмента быстро изнашиваются, что отражается на точности измерений;
б) использование поверхности вершин колеса в качестве мерительной базы требует, чтобы в (5.74) и в (5.78) – (5.80) подставляли достоверное значение 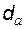 ; это означает, что фактическая величина
; это означает, что фактическая величина 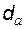 должна быть установлена до измерения хорды, либо на размер
должна быть установлена до измерения хорды, либо на размер 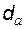 должен быть назначен жесткий допуск.
должен быть назначен жесткий допуск.
Постоянная хорда
Схема измерения показана рис. 5.21, измерительный инструмент – специальный шаблон или тангенциальный зубомер; угол профиля у шаблона обычно равен углу профиля исходного контура a. В этом случае значения измерительных размеров определятся из формул:
постоянная хорда
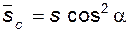 ; (5.83)
; (5.83)
высота от вершины зуба до хорды
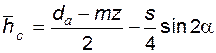 . (5.84)
. (5.84)
Другая версия этих же формул:
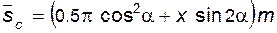 ; (5.85)
; (5.85)
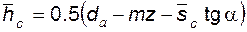 . (5.86)
. (5.86)
При контроле зубьев посредством постоянной хорды исключен кромочный контакт инструмента с измеряемой поверхностью, но сохраняется, как и в предыдущем способе контроля, такой недостаток, как использование поверхности вершин в качестве мерительной базы.
Длина общей нормали
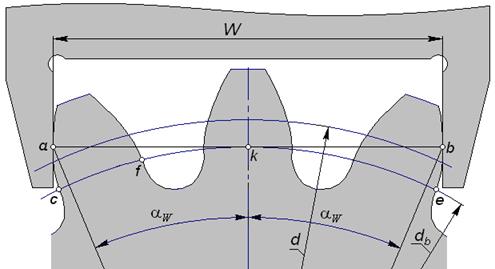 |
| Рис. 5.22 |
На рис. 5.22 построена прямая, касательная к основной окружности эвольвентного колеса. Поскольку любая такая касательная – это нормаль к эвольвенте, то построенная прямая ab является нормалью одновременно к обеим крайним эвольвентам изображенных на рисунке зубьев, т.е. их общей нормалью.
Измеряют общую нормаль с помощью специальной скобы, штангенциркуля, нормалемера. Особенно важно то, что поверхность вершин при измерении как мерительная база не используется. При измерении инструмент охватывает 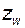 зубьев (на рисунке
зубьев (на рисунке 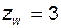 ). Из свойств эвольвенты следует, что
). Из свойств эвольвенты следует, что
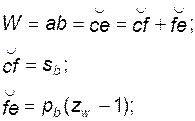
таким образом
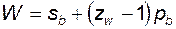 ; (5.87)
; (5.87)
учитывая (5.28) и то, что 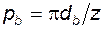 , придадим этой формуле вид
, придадим этой формуле вид
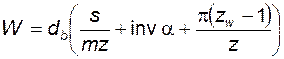 . (5.88)
. (5.88)
Если делительная толщина зуба s не рассчитывалась, то удобнее использовать другую редакцию этой же формулы
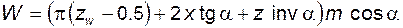 . (5.89)
. (5.89)
Удобно, что зависимости между величинами W, s и x линейные; это позволяет легко устанавливать связь между отклонениями этих величин от номинальных, предусмотренным чертежом или технологической картой. Из (5.88) и (5.89) видно, что
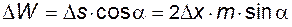 ; (5.90)
; (5.90)
это значит, что если при измерении колеса его размер W оказался, например, увеличенным на 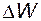 , то, следовательно, соответствующие значения s и x также увеличены по сравнению с требуемыми, причем
, то, следовательно, соответствующие значения s и x также увеличены по сравнению с требуемыми, причем
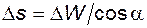 ; (5.91)
; (5.91)
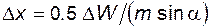 . (5.92)
. (5.92)
При измерении длины общей нормали желательно (хотя и не обязательно), чтобы точки a и b контакта измерительного инструмента и профилей измеряемых зубьев (рис. 5.22) были одинаково удалены от центра колеса, т.е. принадлежали одной окружности. В этом случае угол профиля 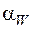 в этих точках (не путать с углом зацепления
в этих точках (не путать с углом зацепления 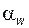 ) определится тем, что
) определится тем, что 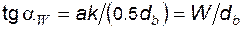 .
.
Поскольку указанные точки a и b должны принадлежать эвольвентным участкам профилей измеряемых зубьев, то при измерении W должно соблюдаться условие 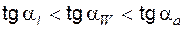 , из которого следуют два неравенства, которыми следует руководствоваться при выборе числа зубьев в длине общей нормали
, из которого следуют два неравенства, которыми следует руководствоваться при выборе числа зубьев в длине общей нормали 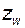 :
:
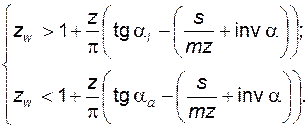 (5.93)
(5.93)
Если никакое целое число 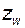 не удовлетворяет одновременно обоим неравенствам (5.93), то измерение длины общей нормали у колеса с такими параметрами невозможно (вместе с тем, это колесо нельзя использовать ни в какой передаче, так как ее коэффициент перекрытия заведомо меньше значения
не удовлетворяет одновременно обоим неравенствам (5.93), то измерение длины общей нормали у колеса с такими параметрами невозможно (вместе с тем, это колесо нельзя использовать ни в какой передаче, так как ее коэффициент перекрытия заведомо меньше значения 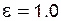 ).
).
Из (5.87) видно, что при изменении 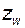 на единицу размер W изменяется на величину
на единицу размер W изменяется на величину  ; это важное свойство нередко используют для косвенного измерения основного шага (например, при отсутствии шагомера).
; это важное свойство нередко используют для косвенного измерения основного шага (например, при отсутствии шагомера).
Вопросы для самопроверки
1. Сформулируйте основной закон зацепления.
2. В каком случае профили, участвующие в зацеплении, называют сопряженными?
3. Определите понятия «линия зацепления» и «полюс зацепления»?
4. Как определить положение границ активной линии зацепления?
5. Что такое эвольвента окружности? Определите понятия: основная окружность, угол профиля, угол развернутости и инволюта угла профиля.
6. Докажите, опираясь на основной закон зацепления, взаимную сопряженность двух эвольвент.
7. Почему кинематика эвольвентного зацепления нечувствительна к изменению межосевого расстояния?
8. Определите понятия «смещение исходного контура» и «коэффициент смещения»?
9. Что такое «коэффициент наименьшего смещения»?
10. В каких случаях зубья колеса считают подрезанными? Заостренными?
11. Охарактеризуйте интерференцию зубьев в зацеплении.
12. Перечислите виды проверок геометрических показателей качества зацепления.
13. Для чего используют измерительные размеры? Виды измерительных зазмеров.
Задачи
Задача 5.01 Для текущей точки эвольвенты Y, расположенной на окружности радиуса 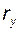 , задан угол развернутости , задан угол развернутости 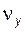 . Полагая диаметр основной окружности . Полагая диаметр основной окружности 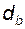 известным, определить известным, определить 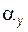 , , 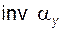 , , 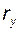 , , 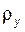 ; написать расчетные формулы в нужной последовательности, указать названия всех перечисленных величин и обозначить их на эскизе. ; написать расчетные формулы в нужной последовательности, указать названия всех перечисленных величин и обозначить их на эскизе. | 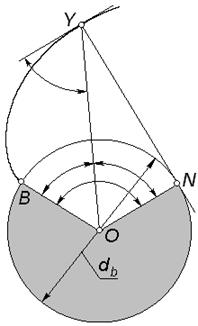 | |
Задача 5.02(см. рисунок к задаче 5.01) Для текущей точки эвольвенты Y, расположенной на окружности радиуса 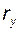 , задан радиус кривизны профиля , задан радиус кривизны профиля 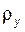 . Полагая . Полагая 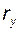 известным, определить диаметр основной окружности известным, определить диаметр основной окружности 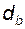 и углы и углы 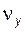 , , 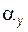 , , 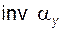 ; написать расчетные формулы в нужной последовательности, указать названия всех перечисленных величин и обозначить их на эскизе. ; написать расчетные формулы в нужной последовательности, указать названия всех перечисленных величин и обозначить их на эскизе. | ||
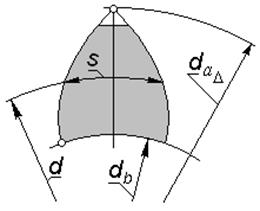 | Задача 5.03 У эвольвентного зубчатого колеса известны диаметры d, 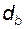 и и 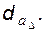 Найти толщину зуба колеса s по дуге делительной окружности; написать все требуемые формулы в порядке их использования, привести названия всех заданных и вычисляемых величин. Найти толщину зуба колеса s по дуге делительной окружности; написать все требуемые формулы в порядке их использования, привести названия всех заданных и вычисляемых величин. | |
Задача 5.04 В точке A эвольвенты, расположенной на окружности радиуса 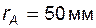 , угол профиля равен , угол профиля равен 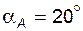 . Чему равен угол профиля в точке С той же эвольвенты, если для нее радиус-вектор . Чему равен угол профиля в точке С той же эвольвенты, если для нее радиус-вектор 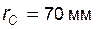 (сделать эскиз)? (сделать эскиз)? | ||
Задача 5.05 В точке Y эвольвенты, расположенной на окружности радиуса 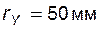 , угол развернутости равен , угол развернутости равен 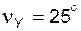 . Чему равен угол развернутости . Чему равен угол развернутости 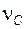 в точке C той же эвольвенты, если для нее радиус-вектор в точке C той же эвольвенты, если для нее радиус-вектор 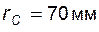 (сделать эскиз)? (сделать эскиз)? | ||||
Задача 5.06 В точке Y эвольвенты, расположенной на окружности радиуса 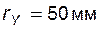 , угол развернутости равен , угол развернутости равен 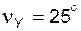 . Определить диаметр . Определить диаметр 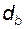 основной окружности эвольвенты (сделать эскиз). основной окружности эвольвенты (сделать эскиз). | ||||
Задача 5.07 Радиус кривизны эвольвенты в некоторой ее точке Y равен 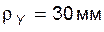 , а угол развернутости – , а угол развернутости – 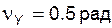 . Определить диаметр . Определить диаметр 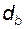 основной окружности эвольвенты и угол профиля в точке Y (сделать эскиз). основной окружности эвольвенты и угол профиля в точке Y (сделать эскиз). | ||||
Задача 5.08 Указать значение угла профиля 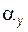 , для которого , для которого 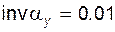 (выбрать верный ответ из пяти предлагаемых): (выбрать верный ответ из пяти предлагаемых): | ||||
| 15.00325°; | 17.57677°; | 0.25764 рад; | 18.47327°; | 0.35677 рад. |
Задача 5.09 Найти значение угла профиля 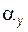 (в градусах) в точке Y эвольвенты, для которой угол развернутости (в градусах) в точке Y эвольвенты, для которой угол развернутости 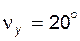 . . | ||||
Задача 5.10 Для колеса, нарезанного стандартным реечным инструментом, заданы: модуль 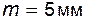 ; диаметр окружности впадин ; диаметр окружности впадин 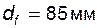 ; диаметр делительной окружности ; диаметр делительной окружности 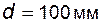 . Определить делительную толщину зуба s. . Определить делительную толщину зуба s. |
Задача 5.11 Для колеса, нарезанного стандартным реечным инструментом, заданы: модуль 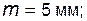 диаметр делительной окружности диаметр делительной окружности 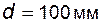 ; делительная толщина зуба ; делительная толщина зуба 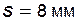 . Определить диаметр окружности впадин . Определить диаметр окружности впадин 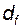 . . |
Задача 5.12 Для колеса, нарезанного стандартным реечным инструментом, заданы: модуль 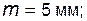 диаметр делительной окружности диаметр делительной окружности 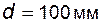 ; диаметр окружности вершин ; диаметр окружности вершин 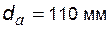 ; делительная толщина зуба ; делительная толщина зуба 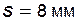 . Определить высоту зуба h. . Определить высоту зуба h. |
Задача 5.13 При нарезании зубьев стандартным реечным инструментом диаметр окружности впадин 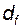 оказался больше расчетного на оказался больше расчетного на 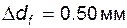 ; рассчитать ожидаемое увеличение делительной толщины зуба ; рассчитать ожидаемое увеличение делительной толщины зуба 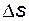 . . |
Задача 5.14 У зубчатого колеса, нарезанного стандартным реечным инструментом, известны: 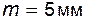 ; ; 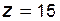 ; ; 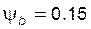 . Определить делительную толщину зуба колеса. Примечание: при написании расчетных формул указывать наименование каждой используемой (включая параметры исходного контура) и вычисляемой величины. . Определить делительную толщину зуба колеса. Примечание: при написании расчетных формул указывать наименование каждой используемой (включая параметры исходного контура) и вычисляемой величины. |
Задача 5.15 У зубчатого колеса, нарезанного стандартным реечным инструментом, известны: 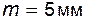 ; ; 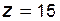 ; ; 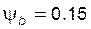 . Определить диаметр окружности заострения. Примечание: при написании расчетных формул указывать наименование каждой используемой (включая параметры исходного контура) и вычисляемой величины. . Определить диаметр окружности заострения. Примечание: при написании расчетных формул указывать наименование каждой используемой (включая параметры исходного контура) и вычисляемой величины. |
Задача 5.16 У зубчатого колеса, нарезанного стандартным реечным инструментом, известны: 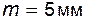 ; ; 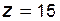 ; ; 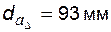 . Определить делительную толщину зуба колеса. Примечание: при написании расчетных формул указывать наименование каждой используемой (включая параметры исходного контура) и вычисляемой величины. . Определить делительную толщину зуба колеса. Примечание: при написании расчетных формул указывать наименование каждой используемой (включая параметры исходного контура) и вычисляемой величины. |
Задача 5.17 Эвольвентное колесо, нарезанное стандартным реечным инструментом, зацепляется с зубчатой рейкой, имеющей прямолинейный профиль зуба и угол профиля 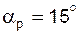 . Диаметр делительной окружности колеса . Диаметр делительной окружности колеса 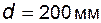 , его угловая скорость , его угловая скорость 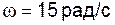 . Определить скорость перемещения рейки. . Определить скорость перемещения рейки. |
Задача 5.18 Эвольвентное колесо, нарезанное стандартным реечным инструментом, модуль которого 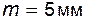 , зацепляется с зубчатой рейкой, имеющей прямолинейный профиль зуба и угол профиля , зацепляется с зубчатой рейкой, имеющей прямолинейный профиль зуба и угол профиля 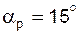 . Определить шаг зубьев рейки . Определить шаг зубьев рейки 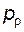 . . |
| Задача 5.19 В эвольвентной зубчато-реечной передаче рейку с углом профиля a = 20° заменили рейкой с углом профиля a¢ = 25°. Как изменится скорость перемещения рейки вдоль ее начальной прямой при сохранении прежнего значения угловой скорости колеса – уменьшится или возрастет (и во сколько раз)? |
Задача 5.20 Зубчатая пара спроектирована на основе стандартного исходного контура и имеет параметры: модуль 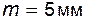 ; числа зубьев ; числа зубьев 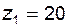 и и 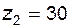 ; межосевое расстояние ; межосевое расстояние 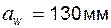 . На сколько миллиметров нужно изменить межосевое расстояние передачи, чтобы ее угол зацепления увеличился по сравнению с имеющимся на 1°? . На сколько миллиметров нужно изменить межосевое расстояние передачи, чтобы ее угол зацепления увеличился по сравнению с имеющимся на 1°? |
Задача 5.21 Зубчатая пара спроектирована на основе стандартного исходного контура и имеет параметры: модуль 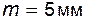 ; числа зубьев ; числа зубьев 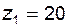 и и 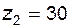 ; диаметры вершин ; диаметры вершин 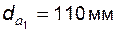 и и 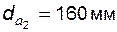 ; межосевое расстояние ; межосевое расстояние 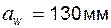 . Определить коэффициент перекрытия передачи. . Определить коэффициент перекрытия передачи. |
| Задача 5.22 С момента входа в зацепление до момента выхода из него профиль каждого зуба какое-то время t участвует в передаче движения. Определить, при каком значении коэффициента перекрытия передачи e однопарное зацепление составляет ровно половину этого времени. |
| Задача 5.23 С момента входа в зацепление до момента выхода из него профиль каждого зуба какое-то время t участвует в передаче движения. Определить, при каком значении коэффициента перекрытия передачи e одну треть в таком случае этого времени составляет двупарное зацепление. |
Заключение
Для успешного усвоения курса «Теория механизмов и машин» большое значение имеет приобретение практических навыков, в том числе умение активно использовать теоретические знания для решения прикладных задач.
Так при решении задач, требующих привлечения графоаналитических методов (построения векторных планов – скоростей, ускорений, сил), вырабатывается умение правильно и рационально записать векторное линейное уравнение и затем грамотно его графически решить.
При решении аналитических задач по кинематическому анализу, синтезу и геометрии зубчатых механизмов и передач вырабатывается видение взаимосвязи рассчитываемых параметров и умение грамотно и в нужной последовательности использовать расчетные формулы и уравнения.
В данном учебном пособии тематика типовых задач в каждом разделе подбиралась авторами так, чтобы решение достаточного их количества позволяло научиться решать подобные задачи в дальнейшем, не испытывая особых затруднений.
Авторы рекомендуют при решении задач постоянно обращаться к теоретическим материалам данного пособия и вопросам для самопроверки.
Список литературы
1. Теория механизмов и машин / Под ред. К.В.Фролова. М.: Высшая школа, 1998. 403 с.
2. Теория механизмов и механика машин / Под ред.К.В.Фролова. М.: Высшая школа, 2002. 664 с.
3. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по теории механизмов и машин. М.: Наука, 1980. 164 с.
4. Планетарные механизмы: Учебное пособие / Болотовский И.А., Васильева О.Ф., Гурьев Б.И., Русак Л.Л. Уфа: Уфимск. гос. авиац. техн. ун-т, 1997. 94с.
5. Цилиндрические эвольвентные зубчатые передачи внешнего зацепления / Болотовский И.А., Гурьев Б.И., Смирнов В.Э. и др. М.: Машиностроение, 1974. 160 с.
6. Справочник по геометрическому расчету эвольвентных зубчатых и червячных передач / Под ред. И.А. Болотовского. М.: Машиностроение, 1986. 448 с.
Борис Иванович Гурьев, Людмила Сергеевна Кутушева, Людмила Леонидовна Русак, Айгуль Ямильевна Садыкова, Регина Шамилевна Хабибуллина
Учебное пособие
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Редактор Медведева Г.Р.
Подписано в печать . Формат 60 × 84 1/16.
Бумага оберточная. Печать плоская. Гарнитура «Ариэль».
Усл. печ. л. 7,1. Усл.-кр. отт. 7,1. Уч. - изд. л. 7,0.
Тираж 100 экз. Заказ №
ГОУ ВПО
Уфимский государственный авиационный технический университет
Редакционно-издательский комплекс УГАТУ
450000, Уфа - Центр, ул. К.Маркса, 12
