Распределения, связанные с повторными испытаниями

Геометрическое распределение.

Рассмотрим схему Бернулли. Обозначим Х – число испытаний до первого успеха, если вероятность успеха в одном испытании р. Если первое испытание успешно, то Х = 0. Следовательно, 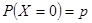. Если Х = 1, т.е. первое испытание неудачно, а второе успешно, то по теореме умножения 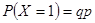. Аналогично, если Х = n , то все испытания до n-ого неудачны и 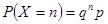. Составим ряд распределения случайной величины Х

				…		…
				…		…

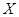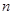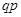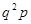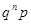Случайная величина с таким рядом распределения имеет геометрическое распределение.

Проверим условие нормировки .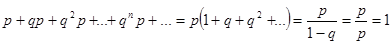

Гипергеометрическое распределение.

Рассмотрим схему испытаний, обобщающую задачу о выборке бракованных деталей и похожую на ситуацию А с N исходами. Пусть имеется n элементов, разделенных на группы: n₁ элементов первого типа, n₂ – второго типа и т.д., n_N – N-ого типа. Какова вероятность, выбрав m элементов, получить среди них m₁ элементов из первой группы, m₂ – из второй и т.д. m_N - из N-ой?

Ее легко вычислить по классическому определению вероятностей с учетом теоремы умножения:

.

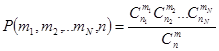В частности, при N=2 (m₂=m-m₁, n₂=n-n₁) (задача о бракованных деталях)

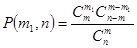
Формула Пуассона и распределение Пуассона.

Пусть число испытаний n велико, вероятность p мала и 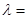np мало. Тогда вероятность наступления m успехов в n испытаниях можно приближенно определить по формуле Пуассона:

.

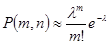Заметим, что по формуле Пуассона можно считать вероятность неуспеха, если q мало, приняв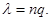

Случайная величина с рядом распределения m, 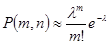имеет распределение Пуассона. Чем больше n, тем формула Пуассона точнее. Для грубых расчетов формулу применяют при n =10, 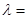0 – 2, при n = 100 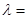0 – 3. При инженерных расчетах формулу применяют при n = 20, 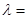0 – 3, n =100, 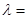0 – 7. При точных расчетах формулу применяют при n = 100, 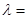0 – 7, n =1000, 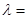0 – 15.

Вычислим математическое ожидание и дисперсию случайной величины, имеющей распределение Пуассона.

,

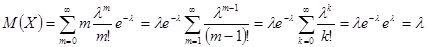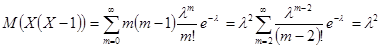
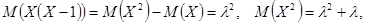
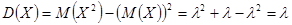
Лекция 5

Экспоненциальное и нормальное распределения.

Экспоненциальное распределение.

Непрерывная случайная величина имеет экспоненциальное распределение, если ее плотность распределения задается формулой

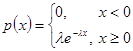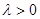, - параметр экспоненциального распределения.

Для случайной величины, имеющей экспоненциальное распределение, , .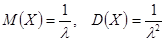

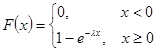Если времена между последовательными наступлениями некоторого события – независимые, экспоненциально распределенные случайные величины с параметром 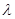, то число наступлений этого события за время t имеет пуассоновское распределение с параметром 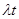. Геометрическое распределение является дискретным аналогом экспоненциального распределения.