Геометрических фигур методом Монте-Карло
Цель работы: получение навыков проведения статистических экспериментов
Общие положення
Имитационная модель – это формальное (то есть выполненное на некотором формальном языке) описание логики функционирования исследуемой системы и взаимодействия отдельных ее элементов во времени, учитывающее наиболее существенные причинно-следственные связи, присущие системе, и обеспечивающее проведение статистических экспериментов.
В результате имитационных экспериментов исследователь получает набор экспериментальных данных, на основе которых могут быть оценены характеристики системы.
Иммитационная модель должна отвечать двум основным требованиям:
– отражать логику функционирования исследуемой системы во времени;
– обеспечивать возможность проведения статистического эксперимента.
В основе статистического эксперимента лежит метод статистических испытаний (метод Монте-Карло). Суть его состоит в том, что результат испытания ставится в зависимость от значения некоторой случайной величины, распределенной по заданному закону. Поэтому результат каждого отдельного испытания также носит случайный характер.
Проведя серию испытаний, получают множество частных значений наблюдаемой характеристики (то есть выборку). Полученные статистические данные обрабатываются и представляются в виде соответствующих численных оценок интересующих исследователя величин (характеристик системы).
Теоретической основой метода статистических испытаний являются предельные теоремы теории вероятностей (теорема Чебышева, теорема Бернулли, теорема Пуассона). Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок при весьма большом числе испытаний.
Важно отметить, что метод статистических испытаний применим для исследования как стохастических, так и детерминированных систем.
Еще одной важной особенностью данного метода является то, что его реализация практически невозможна без использования ЭВМ.
В качестве иллюстрации к изложенному рассмотрим применение метода статистических испытаний для вычисления площади круга заданного радиуса. Данная задача относится к классу детерминированных, поскольку весьма сложно представить себе случайные факторы, под влиянием которых площадь неподвижной геометрической фигуры могла бы изменяться.
Пусть круг имеет радиус r = 5, и его центр находится в точке с координатами О(1, 2). Уравнение соответствующей окружности имеет вид:
(x – 1)2 + (y – 2)2 = 25. (1.1)
Для решения задачи методом Монте-Карло опишем вокруг круга квадрат. Его вершины будут иметь координаты (-4, -3), (6, -3), (-4, 7) и (6, 7). Координаты любой точки, лежащей внутри квадрата или на его границе должны удовлетворять неравенствам: -4 < х < 6 и -3 < у < 7. Квадрат будет иметь длину ребра, равную 10.
При решении данной задачи естественно исходить из того, что все точки в этом квадрате могут появляться с одинаковой вероятностью, то есть будем считать, что х и у распределены равномерно с плотностями вероятностии:
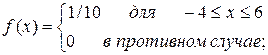(1.2)
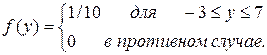(1.3)
Проведя некоторое количество испытаний (то есть получив множество случайных точек, принадлежащих квадрату), подсчитаем число точек, попавших внутрь круга или на окружность. Если выборка состоит из n наблюдений и из n точек m точек попали внутрь круга или на окружность, то оценку площади круга можно получить из соотношения:
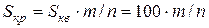. (1.4)
В таблице приведены оценки площади круга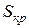 
, полученные для разных значений n, причем для каждого n выполнялось 5 прогонов (точное значение 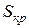= 78,54 см):
Прогоны отличаются друг от друга последовательностями случайных чисел, из которых формировались координаты точек.
На основании полученных результатов могут быть сделаны выводы, которые справедливы для любого имитационного эксперимента независимо от физической природы и типа моделируемой системы:
– каждый прогон модели можно рассматривать как одно наблюдение в проводимом эксперименте на модели;
– с увеличением продолжительности прогона (то есть продолжительности наблюдения) отклонение измеряемой величины от ее точного значения уменьшается, поскольку наблюдаемая система переходит в стационарное состояние;
– влияние переходных условий можно уменьшить, если увеличить количество прогонов модели (то есть количество экспериментов);
– существует предел, за которым увеличение продолжительности прогона модели уже не дает существенного повышения точности результата, измеряемой дисперсией.
Таблица 2.1. – Результаты оценки площади круга методом статических испытаний
| Номер прогона | Оценки площади круга | ||||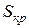
| Число испытаний (n) | |||||
| 1 000 | 5 000 | 10 000 | |||
| 79,5 | 79,5 | ||||
| 78,88 | 78,8 | ||||
| 77,3 | 80,2 | 79,5 | 79,8 | ||
| 79,12 | 71,29 | 78,22 | 78,6 | ||
| 77,72 | 77,76 | 78,26 | |||
| среднее | 75,6 | 78,13 | 76,85 | 79,02 | 78,79 |
| дисперсия | 27,3 | 1,248 | 11,077 | 0,280 | 1,024 |
Основная цель рассмотренного примера – привлечь внимание к тому факту, что имитационное моделирование не ограничивается разработкой модели и написанием соответствующей программы, а требует подготовки и проведения статистического эксперимента. В связи с этим результаты имитационного моделирования следует рассматривать как экспериментальные данные, требующие специальной обработки и анализа.
Задание
Используя метод Монте-Карло определить площадь геометрической фигуры. Найти среднее и дисперсию экспериментальных данных по значениям площади. Сравнить значения полученной площади фигуры с её точным значением, используя для этого математические формулы.
Таблица 1.7 – Варианты заданий
| № ва-рианта | Вид фигуры | |||
| А | В | С | D | |
| Нижняя часть фигуры, образованная окружностью радиуса 2 и кубической параболой | эллипс с центром в начале координат с полуосями а=1, в=2 | Сегмент, образованный окружностью с центром в начале координат радиусом 2 и прямой, проходящей через точки А(2, 0), В(0, 2) | Фигура, образованная параболой у=х2 и прямыми у=0 и х=2 | |
| Фигура, образованная окружностью радиусом 1, параболой у=x2 и прямой y=0 | Фигура, образованная окружностью радиусом 1 и параболой у=x2 | Фигура, образованная параболой у=2x2, гиперболой y=1/x и прямыми у=0 и х=2 | Первая полувол-на синусоиды у=sin x | |
| Фигура, образованная первой полувол-ной синусоиды у=sin x, функцией у=соsx и прямой х=0 | Кольцо с центром в начале координат и радиусом 2 и 1. | Эллипс с центром в начале координат с полуосями а=1, в=2 и вырезанный круг с радиусом 1. | Круг радиуса 1с вырезанным треугольником с вершинами А(-0,5, 0), В(0,5, 0) С(0, 1) | |
| Треугольник с координатами вершин А (1,1), В (2, -2), С (-1, -1) с отверстием в виде вписанной окружностирезанным треугольником с вершинами А() | Фигура, образованная окружностью радиусом 1 и вписанным в него квадратом | Фигура, образованная первой полуволной синусоиды у=sinx и y sin=2x | Фигура, образованная окружностью радиуса 1 с центром в начале координат и окружностью радиуса 0,5 с центром в точке А(0, 0,5) | |
| Объем сферы радиуса 2 | Объем цилиндра диаметра 2 и высотой 1. | Объем конуса с диаметром основания 2 и высотой 2. | Площадь поверхности цилиндра диаметра 2 и высотой 1. | |
| Площадь под кривой, характеризующей плотность нормального распределения со средним, равным 0 и дисперсией 1. | Площадь поверхности пирамиды с квадратным основанием, стороной 1 и высотой 1 | Площадь поверхности конуса с диаметром основания 2 и высотой 2. | Площадь под кривой еxp(-x2) |
Рекомендуемая литература
1. Гультяев А. Имитационное моделирование в среде Windows. Практическое пособие. – СПб.: Корона-принт, 1999.-288с.
2. Максимей И.В. Имитационное моделирование на ЭВМ. М.: Радио и связь, 1988.
3. Технология системного моделирования/Под ред. С.В. Емельянова, В.В. Калашникова и др. М.: Машиностроение; Берлин: Техник, 1988.
4. Советов Б.Я., Яковлев С.А. Моделирование систем. 2-е издание, перераб. и доп. М.: Высшая школа, 1998.
Контрольные вопросы
1. Охарактеризовать методику проведения статистического эксперимента.
2. Расписать метод статистических испытаний (метод Монте-Карло).
3. Как зависит точность эксперимента от количества прогонов модели.
4. В каких случаях целесообразно применять имитационное моделирование.
5. Преимущества и недостатки использования имитационного моделирования.