Основные теоретические положения

Пусть дана в пространстве точка А. Введем три взаимно перпендикулярные плоскости проекций p1, p2, p3 (рис.3.1). Положение точки в пространстве (только в том случае, если введена система координат) однозначно определяется тремя, например, декартовыми (прямоугольными) координатами x, y, z, численные значения которых равны расстояниям, на которые точка удалена от плоскостей проекций, если они совмещены с координатными плоскостями выбранной системы координат. Чтобы определить эти расстояния, необходимо, используя метод ортогонального проецирования, через точку А провести лучи, перпендикулярные плоскостям проекций (называемые проецирующими лучами), затем построить точки А1, А2, А3 пересечения прямых с плоскостями проекций и измерить длины отрезков [AA1], [AA2], [AA3]. Эпюр Монжа, или комплексный чертеж получают путем совмещения плоскостей проекций p1, p2, p3 (рис.3.2) в результате поворота их относительно осей OX и OZ, называемых также осями проекций.

Рис.3.1 Рис.3.2

При этом в начертательной геометрии приняты следующие обозначения и наименования:

p₁, p₂, p₃ – горизонтальная, фронтальная и профильная плоскости проекций соответственно;

А₁, А₂, А₃ – горизонтальная, фронтальная и профильная проекции точки А соответственно;

|AA₃|=|OA_x|=x ; |AA₂|=|OA_y|=y; |AA₁|=|OA_z|=z – соответственно абсцисса x, ордината y и аппликата z точки А;

[AA₁), [AA₂), [AA₃) – проецирующие лучи, перпендикулярные плоскостям проекций.

Линии, связывающие пары проекций, называются линиями связи.

Чертеж, изображенный на рис.3.2, называется трехпроекционным чертежом точки. Можно заметить, что:

- фронтальная А₂ и горизонтальная А₁ проекции точки А всегда располагаются на одной вертикальной линии связи (А₁А₂);

- фронтальная А₂ и профильная А₃ проекции точки А всегда располагаются на одной горизонтальной линии связи;

- линия связи всегда перпендикулярна оси проекций (А₁,А₂ ^ OX; А₂,А₃ ^ OZ);

- две проекции точки однозначно определяют положение точки в пространстве, а, значит, по двум заданным точкам всегда можно построить третью проекцию.

Рис.3.3.

Так как для описания положения точки в пространстве с помощью комплексного чертежа вполне достаточно двух ее проекций (обычно горизонтальной и фронтальной), в задачах начертательной геометрии используют двухпроекционное изображение точки на эпюре (рис. 3.3).

Пример решения задачи на построение эпюра точки

Построить ортогональные (эпюр, двухпроекционный чертеж) и аксонометрические проекции точек А (30,-18,30) и B (15,25, 50), а также:

- точки K, симметричной точке А относительно плоскости p₁;

- точки С, симметричной точке A относительно плоскости p₂;

- точки D, симметричной т. B относительно оси OX;

Аксонометрические проекции точек следует строить во фронтальной диметрической проекции – ГОСТ 2.317-69.

Решение

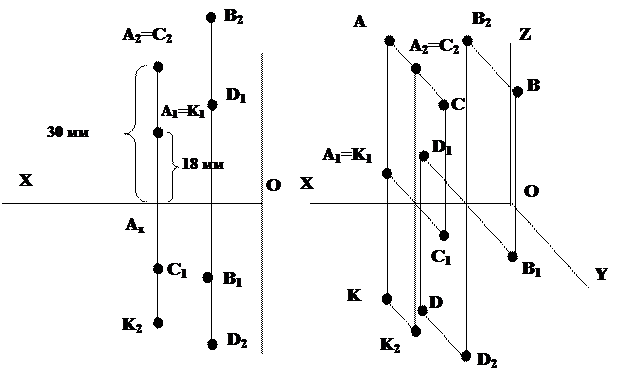
Для построения на эпюре точки А проведем ось OX. От точки О откладываем координату x_A, полученную точку обозначаем A_x (рис.3.4). Через точку A_x проводим линию связи, перпендикулярную оси OX. Вдоль линии связи откладываем координаты z_A=30 мм – выше оси OX (т.к. значение положительно), y_A=18 мм выше оси OX (т.к. значение y отрицательно). В результате координата z_Aопределит положение фронтальной проекции А₂ точки А, а y_A – горизонтальной проекции A₁. Для построения аксонометрической проекции точки А нужно известные координаты отложить вдоль соответствующих осей и далее выполнять построения, очевидные по рис.3.4. Так как в качестве аксонометрической выбрана прямоугольная диметрия, то координата y при построениях уменьшается вдвое.

Рис.3.4

Для определения искомых координат точек, симметричных относительно геометрических объектов заданным, удобно использовать аксонометрическое изображение плоскостей p₁/p₂ под другим углом зрения (рис.5) (вдоль оси OX, ось OX направлена на нас). На рис.3.5, например, можно видеть построение точки D, симметричной т.B относительно оси OX.

Подобное представление удобно для установления связи координат искомых точек К,С, D и М, необходимых для построения их эпюров.

x_K=x_А, y_K=y_A, z_K=-z_A ;

x_С=x_А, y_С=-y_A, z_С=z_A; (1)

x_D=x_В, y_D=-y_В, z_D=-z_В;

В истинности выражений (1) предлагается убедиться самостоятельно.

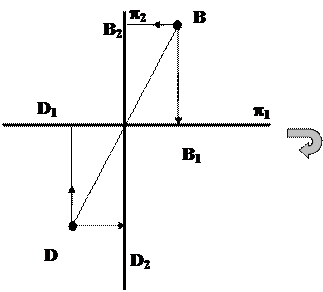Рис.3.5