Натуральный триэдр траектории.

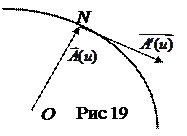Прежде всего несколько разовьем ранее сказанное о вектор-функции и ее производной. Пусть 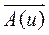- непрерывная вектор-функ­ция скалярного аргумента u, геометрически изображаемая своим годографом, т. е. траекторией конца N векторов 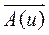при непрерывно изменяющихся значениях аргумента u, и начало этих векторов откладывается от некоторого полюса О (Рис 19). Производная от вектор – функции 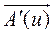по скалярному аргументу u, определяется как предел

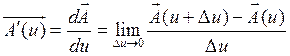(2.1)

и представляет вектор, имеющий направление каса­тельной к годографу, проведенной в сторону, соот­ветствующую возрастанию аргумента u. Вектор 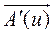характеризует быстроту изменения по величине и направлению век­тора 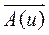с изменением аргумента u.

Величину или модуль производной будем обозначать через 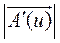. Модуль произ­водной вектора не равен значению производной его модуля.

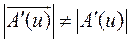(2.2)

При дифференцировании векторов сохраняются те же правила, что и при дифференцировании функций:

производная геометрической суммы (разности) вектор–функции равна геометрической сумме (разности) производных. Точно так же сохраняется и правило дифференцирования произведения скалярной функции X (u) на вектор :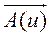

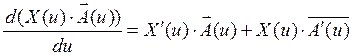
Понятие вектор – функции и её производной облегчают рассмотрение основных геометрических свойств траектории, необходимых для развития представления о скорости и ускорения точки. Рассмотрим некоторую кривую, лежащую (вообще говоря) не в одной плоскости. Возьмём на этой кривой три точки М1, М2 и М. Проведём через эти три точки плоскость (предполагается, что три точки не лежат на одной прямой). Устремим точки М1 и М2 к точке М. Проведённая плоскость при этом будет каким – то образом поворачиваться и займёт предельное положения, когда все три точки сольются. Это предельное положение назовём соприкасающейся плоскостью (СП), в которой проведём касательную к кривой в точке М. Орт касательной в точке М обозначим 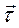. Проведем в точке М плоскость перпендикулярную к орту 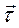, эту плоскость назовём нормальной плоскостью (НП) кривой. Любая прямая, проведенная в этой плоскости через точку М, будет перпендикулярна к 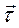, т. е. будет нормалью кривой; линия пересе­чения нормальной и соприкасающейся плоскостей определяет глав­ную нормаль кривой. Иными словами, главной нормалью называется нормаль, лежащая в соприкасающейся плоскости. Нормаль, перпен­дикулярная к главной нормали, называется бинормалью кривой. Если, в частности, кривая — плоская, то соприкасающейся пло­скостью будет плоскость, в которой расположена кривая, а главной нормалью — нормаль кривой, лежащая в этой плоскости.

Совокупность трех взаимно перпендикулярных осей: 1) касатель­ной, направленной в сторону возрастания дуги, 2) главной нормали, направленной в сторону вогнутости кривой, и 3) бинормали, перпендикулярной к касательной и главной нормали образует так называемый натуральней триэдр кривой.

Единичные векторы этих осей обозначим соответственно через 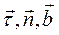. Найдем выражения этих трех единичных векторов натураль­ного триэдра через вектор-радиус точки на кривой, заданный как вектор-функция дуги: 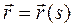. Найдем прежде всего 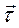. По определению векторной производной вектор 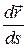направлен по касательной к годографу вектора 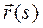в сторону возрастания дуги S. С другой стороны, численная величина производной равна 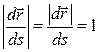. Таким образом, векторная производная представляет искомый единичный вектор касательной

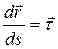(2.3)

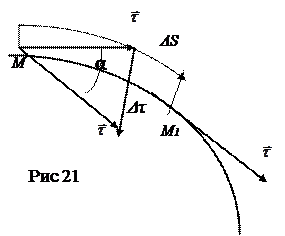Для определения единичного вектора главной нормали 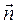обратимся к рис. 20 и рис. 21.

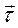Рассмотрим равнобедренный треугольник, обра­зованный векторами . Если точка М1 взята на весьма малом расстоянии ΔS от точки М, то угол α (угол смежности) будет также мал и вектор 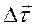, с тем меньшей ошибкой, чем меньше ΔS, можно считать перпендикулярным к 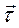и, следова­тельно, параллельным вектору нормали 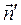, лежащему с 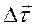в одной и той же плоскости. По абсолютной величине 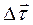(как основание равнобед­ренного треугольника с малым углом α при вершине и боковыми сторонами, равными единице) будет равен 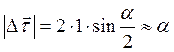Отсюда найдем (с точностью до малых высших порядков): 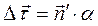или 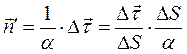. Будем приближать ΔS к нулю, тогда точка M1 будет стремиться к М, единичный вектор нормали 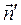— к искомому единичному вектору 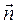, и мы будем иметь: 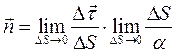. Второй множитель определяет кривизну кривой в данной точке, величина обратная кривизне – ρ называется радиусом кривизны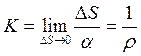

Таким образом, имеем следующее выражение орта главной нормали 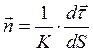. Или в более привычной записи

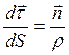(2.4)

Скорость точки.

Пусть за время 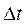точка пройдет по заданной траектории путь 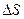, тогда отношение 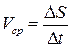характеризует среднюю быстроту изменения пути со временем за интервал 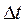или среднюю скорость движения точки за этот интервал. Предел средней скорости за интервал 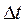, при 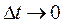, называется скоростью в данный момент t

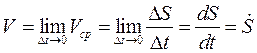
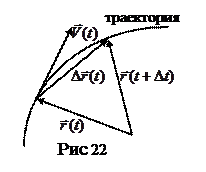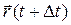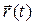Условимся точкой, поставленной над буквой, в дальнейшем обозначать производную по времени. Для того, чтобы определить и направление движения, введём понятие вектора скорости. Пусть и определяют два положения точки на траектории за промежуток времени 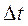(рис. 22). Скоростью точки будем называть

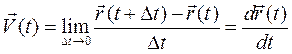или

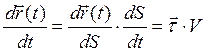(2.5)

Вектор скорости точки равен векторной производной вектор-радиуса точки по времени и направлен по касатель­ной к траектории движения точки. Разложим вектор-радиус 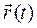по соответствующим осям декартовой системы координат

.

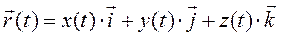Дифференцируя обе части этого равенства по времени и учитывая, что орты постоянны по величине и направлению будем иметь

,

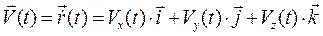что позволяет записать

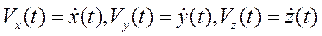. (2.6)

Модуль скорости равен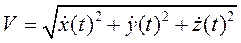

Ускорение точки.

В общем случае движение точки происходит с переменной по величине и по направлению скоростью. Желая охарактеризовать изменение скорости, вводят меру быстроты этого изменения со временем — ускорение, которое должно учитывать векторное (геометрическое) изменение скорости, т. е. изменение ее по величине и по направлению. Для этого рассмотрим (как и для скорости) два значения скорости в моменты времени 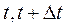, и определим ускорение как

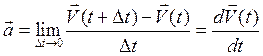(2.6)

Если радиус – вектор представлен разложением по ортам декартовой системы координат

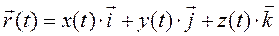, тогда

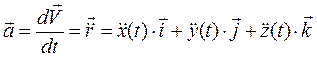
и

.

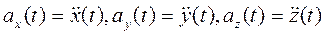Модуль ускорения равен

.

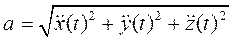Считая 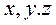координатами точки N – конца вектора 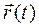, можно рассматривать вектор скорости, согласно (2.5), как скорость конца вектора 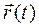, а считая 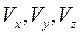- координатами точки М – конца вектора 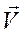, можно рассматривать вектор ускорения, как скорость конца вектора 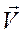. Применяя полученные выражения единичных вектором осей натурального триэдра траектории, найдем составляющие вектора ускорения по этим осям. Вспомнив, что вектор ускорения есть производная по времени от вектора скорости, получим

,

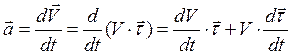но 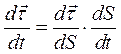, откуда следует

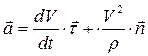(2.7)

Равенство (2.7) представляет собой разложение вектора уско­рения по осям натурального триэдра. Обозначив коэффициенты при единичных векторах, 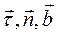и записав проекции ускорения на оси натурального триэдра, соответственно через 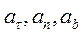будем иметь:

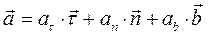
причем из (2.7) следует, что

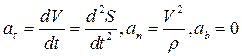
Последнее равенство говорит о том, что вектор ускорения пер­пендикулярен к бинормали, т. е. ускорение лежит в соприкасаю­щейся плоскости. Первое слагаемое в разложении (2.7) - 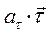дает касательную (тангенциальную) составляющую ускорения, второе 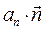- нормаль­ную составляющую ускорения. Иногда для кратко 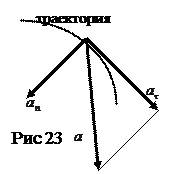сти их называют просто касательным и нормальным ускорением. В случае ускоренного движения знак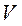и и 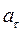одинаковы, в случае замедленного движения - противоположны, т. е. при ускоренном движении касательное ускорение направлено в ту же сторону, что и вектор скорости, а при замедленном движении имеет направление, противоположное скорости (рис. 23).

Итак, вектор ускорения в криволинейном движении может быть представлен как геометрическая сумма двух ускорений: касательного и нормального. Величина ускорения может быть представлена так:

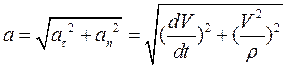
Рассмотрим два частных случая:

а) Случай равномерного движения; величина скорости постоянна, так что 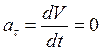, и величина ускорения равна в этом случае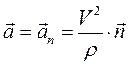

б) Случай прямолинейного движения; кривизна прямой линии равна нулю и, следовательно, 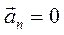, и .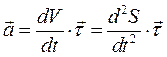

Из сопоставления этих двух случаев следует, что в равномерном прямолинейном движении ускорение равно нулю.

Отметим, что не следует смешивать 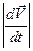и 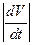так как первое выражение определяет величину полного ускорения, а второе - абсолютное значение лишь одной его касательной составляющей. На различие этих величин указывалось уже выше (формула (2.2)). Разложение ускорения на касательную и нормальную части имеет простое кинематическое значение. Вектор ускорения, определяющий быстроту изменения вектора скорости по величине и направлению, представляется суммой касательного ускорения, характеризующего изменение величины скорости, и нормального, характеризующего изменение ее по направлению.