Гаврилов Г.П. Сборник задач по дискретной математике / Г.П. Гаврилов, А.А. Сапоженко.-М.: Наука, 1977, 1991 (2-е изд.,перераб. и доп.), 2004 (3-е изд.,перераб.)
Лабораторные работы по дискретной математике.
Ф.И.О.: Смирнов В.В.
Группа:ИТСС-12
Теоретическая часть.
F(x,y,z)=(01101111)
Представить всеми способами.
Представить в виде СДНФ и СКНФ.
Представить в виде полинома Жегалкина двумя способами.
Найти существенные и фиктивные переменные двумя способами.
Разложение по переменным x и z.
Выяснить, является ли данная функция шефферевой. Если нет, то какую одну функцию надо добавить к ней, чтобы получить полную систему. Единственным ли образом это можно сделать?
Представить всеми способами.
Аналитический способ.
xz+xy+x+y+z
Табличный способ.
| x,y,z | f(x,y,z) |
Векторный способ.
h(x,y,z)=(01101111)
Через область единичных или нулевых значений.
h(x,y,z)=∑1(1,2,4,5,6,7)=∑0(0,3)
Графический способ.
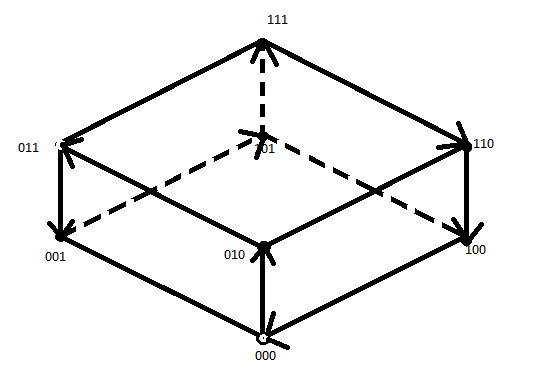
Через коды Грея.
f(x,y,z):Г3:000,010,011,001,101,111,110,100.
f(x):Г1:01.
f(x,y):Г2:00,01, 11,10.
Через карты Карно.
{x,y,z}={x} 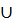 {y,z}={x,y}
{y,z}={x,y} 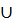 {z}={x}
{z}={x} 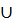 y
y 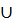 {z}
{z}
А)
| y,z x | ||||
Б)
| x,y z | ||||
В)
| x,z y | ||||
Представить в виде СДНФ и СКНФ.
| x,y,z | f(x,y,z) |
СКНФ:f(x,y,z)=&(xδ1˅yδ2˅zδ3)= (x˅y˅z)(x˅ 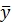 ˅
˅  )
)
(δ1,δ2,δ3)
f(δ1,δ2,δ3)=0
СДНФ:f(x,y,z)=˅xδ1&yδ2&zδ3= x͞yz˅ 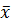 y
y  ˅x
˅x 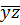 ˅x
˅x 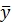 z˅xy
z˅xy  ˅xyz
˅xyz
(δ1,δ2,δ3)
f(δ1,δ2,δ3)=1
Представить в виде полинома Жегалкина двумя способами.
Метод таблиц.
f(x,y,z)=(01101111)=a1xyz+a2xy+a3xz+a4yz+a5x+a6y+a7z+a8
1. f(000)=0: a8=0
2. f(001)=1: a7+a8=1óa7=1
3. f(010)=1: a6+a8=1óa6=1
4. f(011)=0: a4+a6+a7+a8=0ó a4+1+1=0óa4=0
5. f(100)=1: a5+a8=1óa5=1
6. f(101)=1: a3+a5+a7+a8=1óa3+1+1=1óa3=1
7. f(110)=1: a2+a5+a6+a8=1óa2+1+1=1óa2=1
8. f(111)=1: a1+ a2+ a3+ a4+a5+a6+ a7+a8=1ó a1+1+1+1+1+1=0óa1=0
Вывод: f(x,y,z)=xz+xy+x+y+z
Метод неопределенных коэффициентов.
∑xδ1yδ2zδ3= 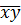 z+
z+ 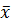 y
y  +x
+x 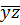 +x
+x 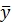 z+xy
z+xy  +xyz=
+xyz= 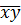 z+
z+ 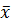 y
y  +x
+x 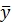 (
(  +z)+xy(
+z)+xy(  +z)=
+z)= 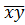 z+
z+ 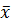 y
y  +x
+x 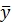 +xy=
+xy=
(δ1,δ2,δ3) 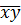 z+
z+ 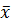 y
y  +x(
+x( 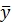 +y)=
+y)= 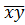 z+
z+ 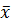 y
y  +x=(x+1)((y+1)z+y(z+1))+x=(x+1)(yz+z+yz+y)
+x=(x+1)((y+1)z+y(z+1))+x=(x+1)(yz+z+yz+y)
f(δ1,δ2,δ3)=1 +x=(x+1)(z+y)+x=xz+xy+z+y+x
Найти существенные и фиктивные переменные двумя способами.
Метод таблиц.
x: f(0,λ2,λ3)≠f(0,λ2,λ3)
f(000)≠f(100)=>x существенный
y: Ǝ 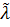 =(λ1,λ3),что f(λ1,0,λ3)≠f(λ1,0,λ3)
=(λ1,λ3),что f(λ1,0,λ3)≠f(λ1,0,λ3)
Ǝ 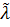 =(0,0),что f(000)≠f(010)=>y существенный
=(0,0),что f(000)≠f(010)=>y существенный
Z: Ǝ 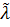 =(λ1,λ2),что f(λ1,λ2,0)≠f(λ1,λ2,1)
=(λ1,λ2),что f(λ1,λ2,0)≠f(λ1,λ2,1)
Ǝ 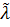 =(0,0),что f(000)≠f(001)=>z существенный
=(0,0),что f(000)≠f(001)=>z существенный
Метод эквивалентных преобразований.Записать функцию в аналитической форме СДНФ.
f(x,y,z)= 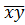 z˅
z˅ 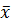 y
y  ˅x
˅x 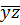 ˅x
˅x 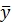 z˅xy
z˅xy  ˅xyz=
˅xyz= 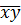 z˅
z˅ 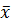 y
y  ˅x
˅x 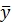 (
(  ˅z)˅xy(
˅z)˅xy(  ˅z)=
˅z)= 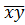 z˅
z˅ 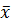 y
y  ˅x
˅x 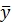 ˅xy=)=
˅xy=)= 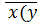 z˅y
z˅y  )˅x(
)˅x( 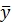 ˅y)=
˅y)= 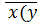 z˅y
z˅y  )˅x
)˅x
Разложить по переменным x и z.
f(x,y,z)=˅xδ1&zδ2f(δ1,y,δ2)=x0z0f(0,y,0)˅x0z1f(0,y,1)˅x1z0f(1,y,0)˅x1z1f(1,y,1)= 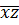 f(o,y,o)˅
f(o,y,o)˅ 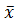 zf(
zf(
( 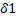 ,δ2)
,δ2)
0,y,1)˅x  f(1,y,0)˅xzf(1,y,1)=
f(1,y,0)˅xzf(1,y,1)=
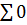 xδ1zδ2f(δ1,y,δ2)=
xδ1zδ2f(δ1,y,δ2)= 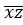 f(0,y,0)+
f(0,y,0)+ 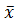 zf(0,y,1)+x
zf(0,y,1)+x  f(1,y,0)+xz(1,y,1)=
f(1,y,0)+xz(1,y,1)=
(δ1,δ2)
=&( 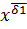 ˅
˅ 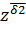 ˅f(δ1,y,δ2))=(
˅f(δ1,y,δ2))=( 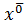 ˅
˅ 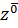 ˅f(0,y,0))&(
˅f(0,y,0))&( 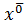 ˅
˅ 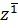 ˅f(0,y,1))&(
˅f(0,y,1))&( 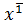 ˅
˅ 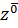 ˅f(1,y,0))&(
˅f(1,y,0))&( 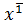 ˅
˅ 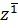 ˅f(1,y,1))=(x˅z˅f(o,y,o))(x˅
˅f(1,y,1))=(x˅z˅f(o,y,o))(x˅  ˅f(0,y,1))(
˅f(0,y,1))( 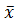 ˅z˅f(1,y,0))(
˅z˅f(1,y,0))( 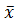 ˅
˅  ˅f(1,y,1))
˅f(1,y,1))
f(x,y,z)= (x˅z˅y)(x˅  ˅y) (
˅y) ( 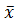 ˅z˅1)(
˅z˅1)( 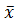 ˅
˅  ˅1)
˅1)
f(0,y,0)=y
f(0,y,1)= 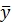
f(1,y,0)= 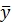
f(1,y,1)= 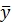
Выяснить, является ли данная функция шефферевой. Если нет, то какую одну функцию надо добавить к ней, чтобы получить полную систему. Единственным ли образом это можно сделать?
6.1)
| x,y,z | h(x,y,z) |
| T0 | T1 | S | M | L | |
| h(x,y,z) | + | + | - | - | - |
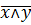 | - | - | |||
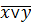 | - | - | |||
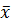 | - | - |
h ϵ T0 т.к. h(0,0,0)= 0.
h ϵ T1 т.к. h(1,1,1)=1.
h ϵ S т.к. h(0,0,0)≠h(1,1,1).
h ϵ M т.к. (0,1,1)≥(0,1,0).
Для того, что бы понять h не ϵ L, надо полиному Жигалкина.
h(x,y,z)= xz+xy+z+y+x
h ϵ L т.к. h(x,y,z)=xz+xy+x+y+z
h(x,y,z) не является шефферевой, т.к. h ϵ T0,T1.
6.2)
Добавляем f которая ϵ Т0,T1, где f(x,y,z)= 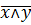 .
.
[{h,f}]=P2 по теореме о полноте.
6.3)
Получить полную систему можно не единственным образом т.к. можно добавить не одну функцию, а несколько, например: 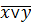 ,
, 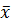 .
.
Литература
Яблонский, С.В. Введение в дискретную математику/ С.В.Яблонский. –М.: Наука, 1979, 1986 (2-у изд., перераб. И доп.),2001(3-е изд.,стер.).
Гаврилов Г.П. Сборник задач по дискретной математике / Г.П. Гаврилов, А.А. Сапоженко.-М.: Наука, 1977, 1991 (2-е изд.,перераб. и доп.), 2004 (3-е изд.,перераб.).
3) Михеева, Е.А. Индивидуальные задания для математического практикума на ЭВМ по <<Дискретной математике>>: методические указания / Е.А.Михеева.- Ульяновск: фМГУ, 1995.- 49 с.
