Используя условие прочности по нормальным напряжениям подберем № двутавра.

Расставим и определим все опорные реакции.

Для этого необходимо составить и решить два уравнения статики:

Σmom_AF_i=0

F*2-g×2*1-M+4*R_b=0

R_В = (40*2+20+50)/4=-2.5 (кН)

Σmom_ВF_i =0

F*6-g*5-M-R_A *4=0

R_A =(2*40-100-50)/4=22.5 (кН)

После определения опорных реакций необходимо выполнить проверку правильности их определения (спроецировав все силы на вертикальную ось y).

Проверка:

Σпр_уF_i=0

R_A + R_b+ g *2-F=0

-2.5+22.5+20-40=0

0=0 => опорные реакции найдены, верно.

Разобьем балку на участки и рассмотрим каждый в отдельности.

Опр: Участком называется часть балки на которой нет ни сосредоточенных сил ни моментов, а распределенная нагрузка меняется по одному и тому же закону. На границах участков всегда приложены либо сосредоточенная сила либо момент, может начинаться или заканчиваться распределенная нагрузка.

первый участоук. 0≤ u₁≤ 2м

Q_у1 =-(F-qu₁ )=-40+10 u₁- уравнение прямой.

u1
QY1	-40	-20

M_x1 = - ( F * u₁ - q u₁* u₁ /2 ) = q * u₁² /2 – F * u₁- уравнение параболы

Исследуем уравнение на экстремум:

M_x1 =5* u₁² – 40* u₁

M_x1 ٰ = 10* u₁ – 40

10 u₁ - 40 = 0

u₁ = 4м (Не входит в пределы первого участка) (Точка минимума)

M_х1 ^''= 10 => ветви параболы направлены вверх

u1
Mx1		-60

второй участок. 0≤ u₂ ≤ 2м

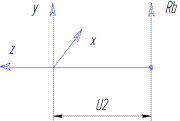
Q_у2 = - (R_B) = - R_B =2.5кH – уравнение прямой параллельной нулевой линии.

M_x2 = - (-R_B*u₂ ) = R_B* u₂ = -2.5* u₂ - уравнение прямой.

u2
Mx2		-5

третий участок. 0≤ u₃ ≤ 2м

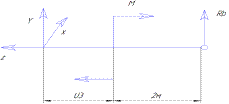
Q_у3 = - (R_B )= - R_B = 2,5 кН – уравнение прямой параллельной нулевой линии.

M_x3 = - (- R_B (u₃ +2)+ М) = R_B * u₃ + R_B *2 – М = -2,5 *u₃ – 5 – 50 = =-2,5 *u₃ -55 – уравнение прямой

U3
Mx3	-55	-60

По решению аналитических выражений на всех участках, получаем, что при действии на балку внешних силовых факторов, в её поперечном сечении возникают два внутренних силовых фактора Q_у и M_x.

Построим Эпюры В.С.Ф. Q_у и M_x. (см. рис.1.)

Используя условие прочности по нормальным напряжениям подберем № двутавра.

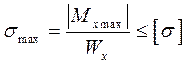
, где M_{x max} – максимальное значение изгибающего момента, на эпюре M_x=60*10⁶ (Н*мм)

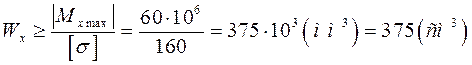
По найденному значению осевого момента сопротивления изгибу из таблицы сортамента выбираем № двутавра (27) W_{x табл} = 371 (см³)

W_{x табл} < W_{x расч.}

W_x двутавра № 27 меньше расчётного значения, но близко к нему.

Рассчитаем какое будет перенапряжение.

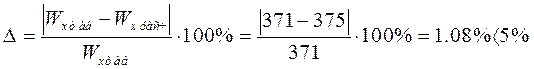
Так как расхождение меньше 5%, что допустимо в инженерных расчетах то выбираем двутавр №27.

Если получилось, что перенапряжение больше 5% то необходимо выбрать двутавр большего поперечного сечения и принять его окончательно.

3. Проверим выбранное сечения на прочность по касательным напряжениям. (по ф-ле Журавского)

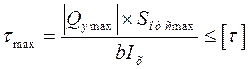, где Q_{y max} максимальное значение поперечной силы, взятое с эпюры Q_{y .} Q_{y max} = 40*10³ (МПа)

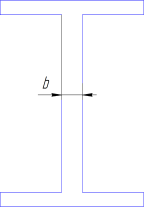
Следующие величины в формуле, берем из таблицы САРТАМЕНТА для выбранного нами ранее двутавра №27: рис.2.

S_{отс max} –максимальный статический момент отсечённой части (момент полусечения). S_{отс max} = 210*10³ (МПа)

I_х- момент инерции сечения относительно оси х. I_х = 5010*10⁴ (мм⁴)

b- ширина ножки двутавра (см. рис.2). b= 6 (мм)

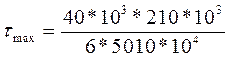=27,9 (МПа)

Получаем, что расчетное напряжение τ_max меньше допускаемого [τ] =100 (МПа), значит выбранный ранее двутавр №27 проходит.

Если получилось, что 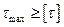то необходимо выбрать двутавр большего поперечного сечения и подставив в формулу новые значения b, I_х, S_{отс max} сделать перерасчет.