Позиционные задачи. пересечение прямой
С ПЛОСКОСТЬЮ, ДВУХ ПЛОСКОСТЕЙ
В общем случае задача на пересечение прямой с плоскостью решается следующим образом. В плоскости отмечается прямая, лежащая в одной проецирующей плоскости с заданной прямой. Точка пересечения этих прямых и будет искомой точкой пересечения прямой с плоскостью.
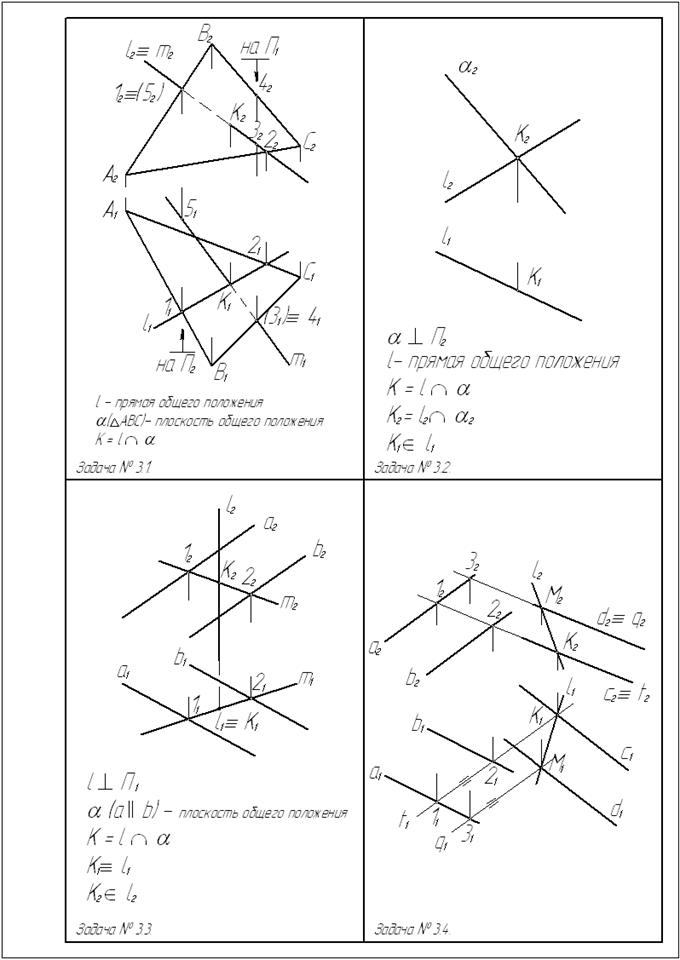
Задача № 3.1. Построить точку К пересечения прямой l с плоскостью a(DABC).
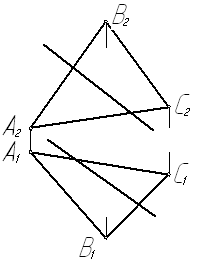
Рис. 13
Отметим в плоскости aпрямую m, которая лежит в одной фронтально проецирующей плоскости с заданной прямой l. Фронтальные проекции этих прямых совпадают. Горизонтальная проекция прямой m построена с помощью точек 1 и 2, принадлежащих плоскости a.
Сначала определяем горизонтальную проекцию К1 точки К в пересечении l1 и m1. Фронтальную проекцию К2 точки К находим по принадлежности точки К прямой l.
При решении задачи можно воспользоваться и такой прямой плоскости a,которая лежит в одной горизонтально проецирующей плоскости с заданной прямой l. В этом случае на эпюре совпадут горизонтальные проекции прямой l и прямой, принадлежащей плоскости a.
Считая DАВС непрозрачной пластиной, покажем видимость прямой l. Для определения видимости относительно плоскости П1 отметим на скрещивающихся прямых l и ВС точки 3 и 4, у которых горизонтальные проекции 31 и 41 совпадают. Точка 3, принадлежащая прямой l, ниже точки 4 прямой ВС, о чем можно судить по фронтальным проекциям 32 и 42. Из этого следует, что прямая l слева от точки К находится над треугольником и при рассматривании сверху будет видимой. В точке К видимость изменяется. Справа от точки К прямая l находится под треугольником и будет невидимой. Горизонтальная проекция невидимой части прямой изображена штриховой линией.
Видимость прямой l относительно плоскости П2 определена с помощью точек 1 и 5.
Задача № 3.2. Построить точку К пересечения прямой lс фронтально проецирующей плоскостью a.
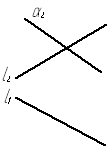
Рис. 14
В этом случае сначала отмечается фронтальная проекция К2 точки К в пересечении l2 с a2.Горизонтальная проекция К1 точки К находится по принадлежности точки К прямой l
Задача № 3.3. Построить точку К пересечения прямой l, которая перпендикулярна плоскости проекций П1, с плоскостью a.
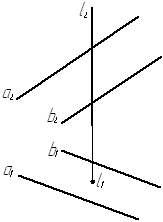
Рис. 15
Здесь К1 º l1, а К2 определяется по принадлежности точки К плоскостиa(аççb) с помощью прямой m.
Задача № 3.4. Построить прямую l пересечения плоскостей a(аççb) и β(сççd)
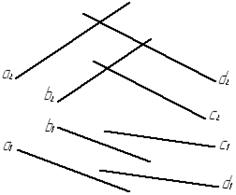
Рис. 16
Линией пересечения двух плоскостей является прямая, для построения которой достаточно найти две точки, общие обеим плоскостям. Каждая из этих точек может рассматриваться как точка пересечения прямой одной плоскости с другой плоскостью.
Следовательно, решение задачи на построение линии пересечения двух плоскостей сводится в основном к двукратному решению задачи на определение точки пересечения прямой с плоскостью.
Прямая l проведена через точки К и М. Точка К определена как точка пересечения прямой плоскости β с плоскостьюa, а точка М - как точка пересечения прямой d плоскости β с плоскостью a. Следует обратить внимание на то, что t1ççq1, так как прямые t и q, принадлежащие плоскости a, параллельны, потому что параллельны их фронтальные проекции t2 и q2.
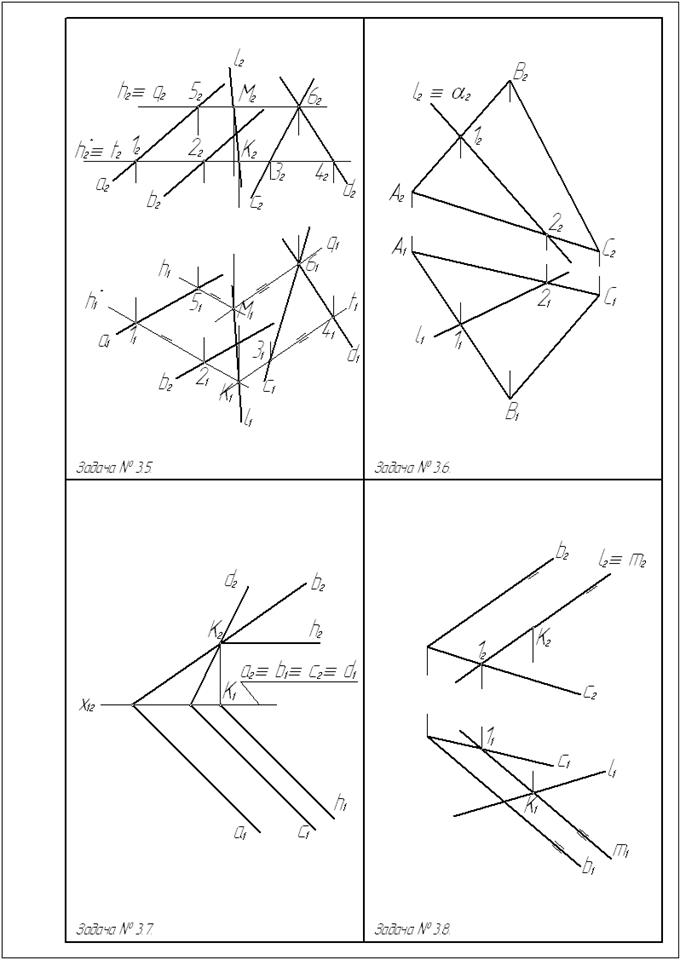
Задача № 3.5. Построить прямую l плоскости a(аççb) с плоскостью β(сÇd)
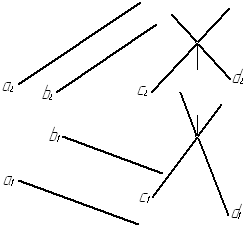
Рис. 17
Для построения прямой линии l пересечения двух плоскостей a и β необходимо найти две общие для них точки К и М.
Чтобы построить точку К, в плоскости a строим горизонталь h (h1, h2) и пересекаем эту прямую с плоскостью β, а вторая общая точка М находится в пересечении второй горизонтали h*, лежащей в плоскости a с плоскостью β.
Задача № 3.6. Построить прямую l пересечения плоскости a^ П2 с плоскостью β (DАВС).
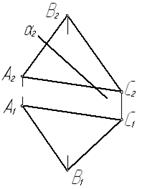
Рис. 18
Плоскость a является фронтально проецирующей. Фронтальная проекция l2 линии пересечения плоскостей совпадает с фронтальной проекцией плоскости a, а горизонтальная проекция построена исходя из условия принадлежности прямой l плоскости β.
Задача № 3.7. Построить прямую h пересечения плоскости a(аÇb) с плоскостьюβ ( с Çd)
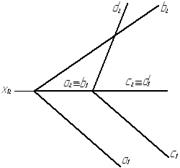
Рис. 19
Плоскость a задана двумя пересекающимися линиями уровня: горизонталью а и фронталью b, а плоскость β задана горизонталью с и фронталью d, по условию горизонталь а параллельна горизонтали с, следовательно линия пересечения этих двух плоскостей тоже будет горизонталь h параллельная горизонталям а и с.
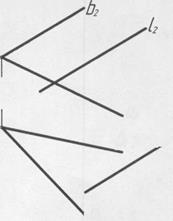 |
Задача № 3.8. Построить точку К пересечения прямой l c плоскостью a(аÇb).
Рис. 20
В плоскости a(аÇb) строится прямая m, лежащая в одной фронтально проецирующей плоскости с прямой l, на эпюре l2ºm2, точка К1= l1Çm1, а точки К2Î l2.
Решения типовых задач раздела 3. приведены на с. 27, 28.
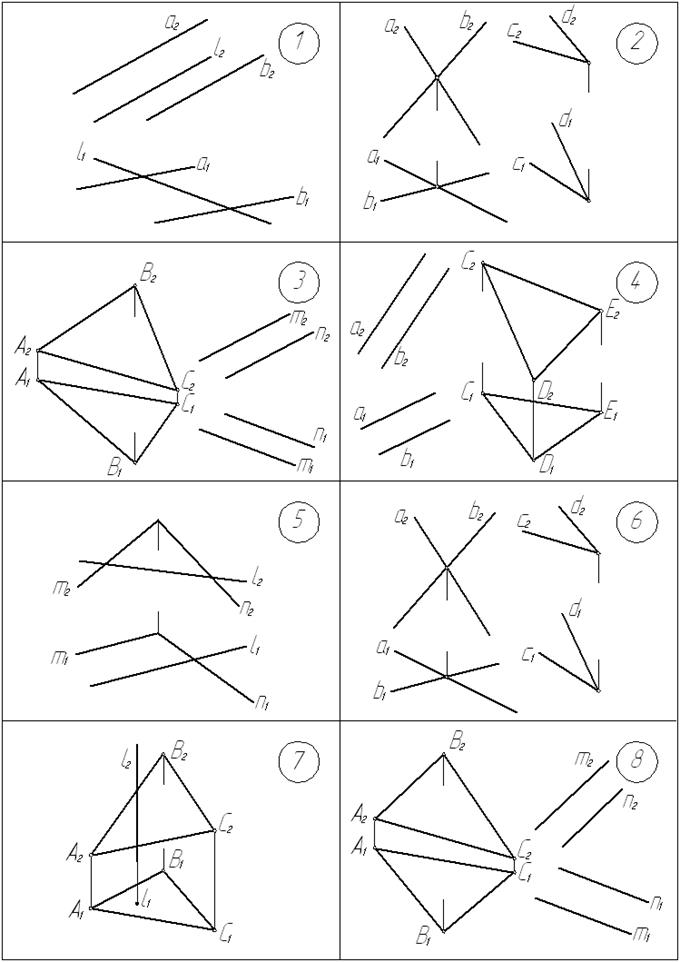
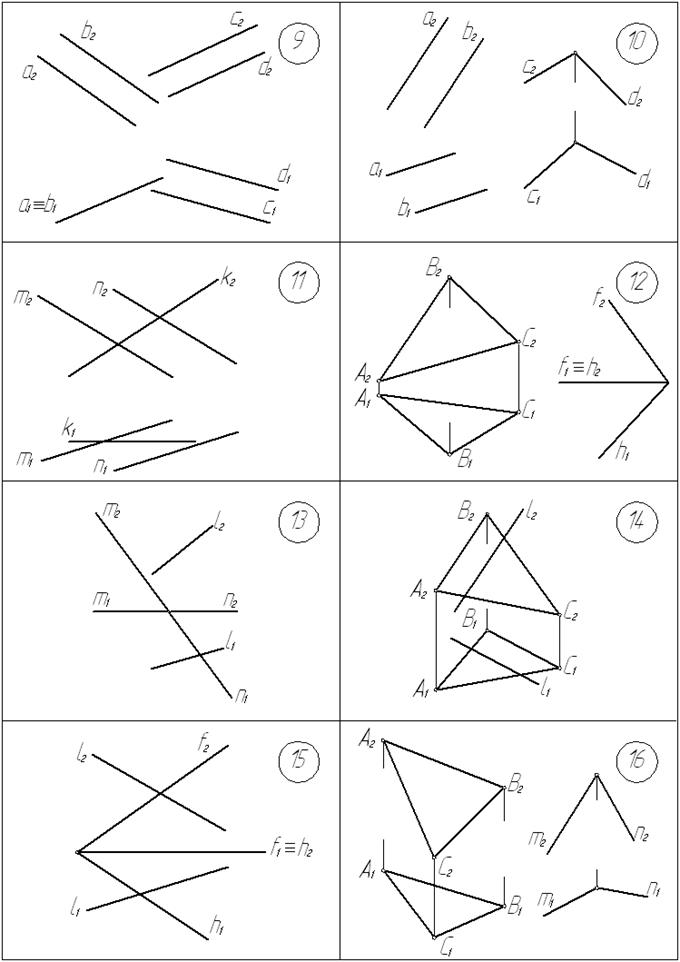
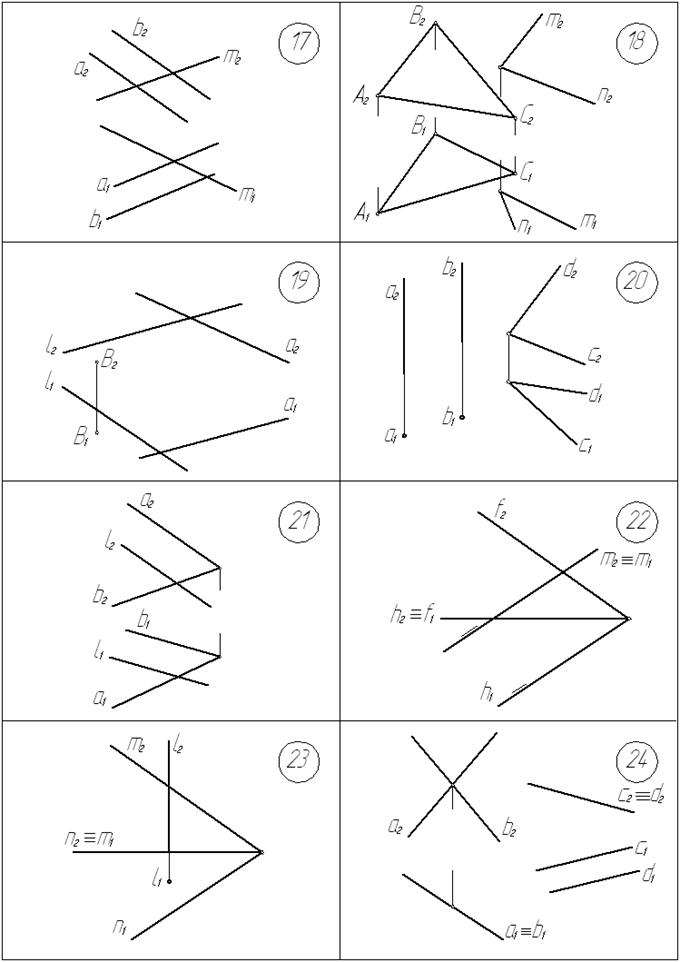
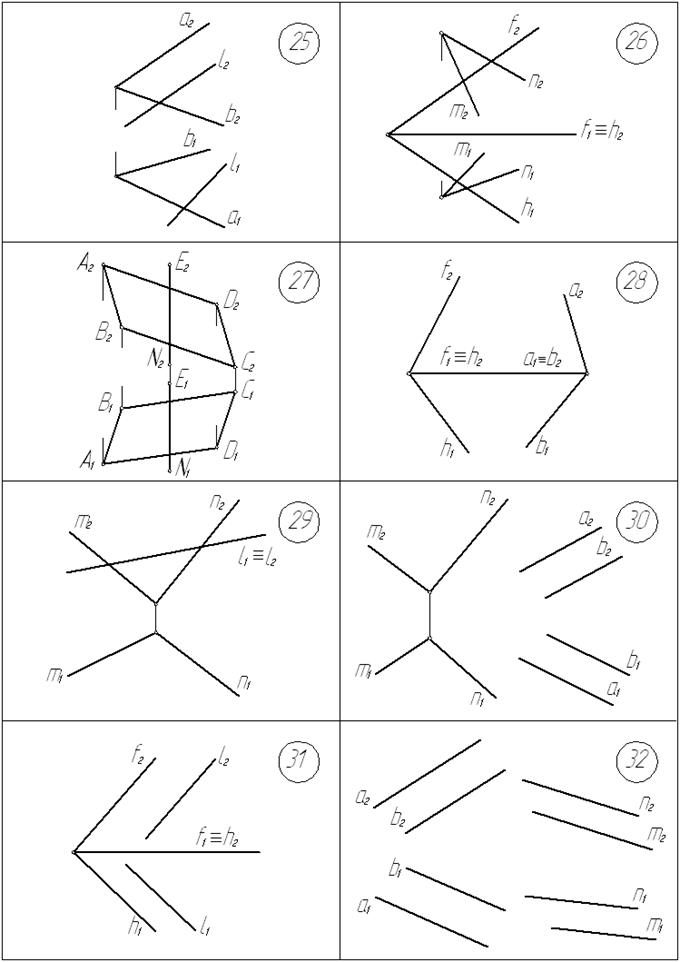
Графические условия задач приведены на с. 30… 33.
Построить точку пересечения К прямой l с плоскостью a в задачах №№ 1,5,7, 11,13,14,15,17,19,21,22,23,25,27,29,31; в задачах № 7,14,27 отметить видимость прямой l относительно плоскости a.
Построить линию пересечения l двух заданных плоскостей a и β в задачах № 2,3,4,6,8,9,10,12,16,18,20,24,26,28,30,32.