Лемма о параллельном переносе силы

Докажем лемму:

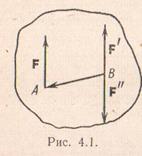Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.

Пусть в точке А твердого тела приложена сила F. Приложим теперь в точке В тела систему двух сил F' и F", эквивалентную нулю, причем выбираем F'= F (следовательно, F"= – F). Тогда сила F=(F, F', F"), так как (F', F")=0.

Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна F' и паре сил (F, F"). Момент пары (F, F") равен

М=М(F, F")=ВА×F,

т.е. равен моменту силы Fотносительно точки В

М=М_В(F).

Таким образом, лемма о параллельном переносе силы доказана.

Основная теорема статики

Введем определения. Пусть дана произвольная система сил (F₁, F₂, F₃, … ,F_n). Сумму этих сил

F=Σ F_k

называют главным вектором системы сил.

Сумму моментов сил относительно какого-либо полюса (центра приведения) называют главным моментом рассматриваемой системы сил относительно этого полюса.

Пользуясь теперь леммой о параллельном переносе силы, докажем следующую основную теорему статики (теорема Пуансо):

Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.

Следовательно, основная теорема статики устанавливает закон эквивалентной замены произвольной системы сил более простой системой, состоящей из одной силы и одной пары.

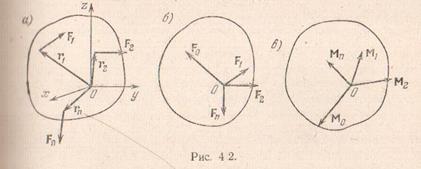
Пусть О – центр приведения, принимаемый за начало координат, r₁, r₂, r₃, … , r_n – соответствующие радиусы-векторы приложения сил F₁, F₂, F₃, … , F_n, составляющих данную систему сил. Прежде всего перенесем силы F₁, F₂, F₃, … ,F_n в точку О, а затем сложим эти силы как сходящиеся; в результате получим одну силу:

F₀=F₁+F₂+…+F_n=Σ F_k,

которая равна главному вектору. Но при последовательном переносе сил F₁, F₂, F₃, … ,F_n в точку О мы получаем каждый раз соответствующую пару сил (F₁, F₁"), (F₂, F₂"), … , (F_n, F_n").

Моменты этих пар соответственно равны моментам данных сил относительно точки О:

М₁=М(F₁, F₁")=r₁×F₁=М_О(F₁),

М₂=М(F₂, F₂")=r₂×F₂=М_О(F₂),

………………………………….

М_п=М(F_n, F_n")=r_n × F_n =М_О(F_n). (4.1)

На основании правила приведения системы пар к простейшему виду все указанные пары можно заменить одной парой. Ее момент равен сумме моментов всех сил системы относительно точки О, т.е. равен главному моменту, так как согласно формулам (3.18)

М_О=М₁+М₂+ … +М_n = М_О(F₁)+М_О(F₂)+ … +М_О(F_n)=

= Σ М_О(F_k)=Σ r_k× F_k.

Итак, систему сил, как угодно расположенных в пространстве, можно в произвольно выбранном центре приведения заменить силой

F_О=Σ F_k (4.2)

и парой сил с моментом

М_О= Σ М_О(F_k)=Σ r_k× F_k. (4.3)

Не следует считать, что главный вектор и главный момент имеют чисто формальное значение и что их можно найти только с помощью вычислений. Очень часто отдельно действующие на тело силы нельзя определить даже опытным путем, в то время как главный момент и главный вектор находятся сравнительно просто. Поясним это примером. Рассмотрим вал, находящийся в подшипниках скольжения. При вращении вала на точки его поверхности действуют со стороны подшипника силы трения. Число точек контакта и модули сил трения, как правило, не известны. Не всегда их можно определить и с помощью эксперимента, однако простым измерением находится сумма моментов всех сил трения относительно оси вращения, т.е. главный момент сил трения.

По тем же соображениям момент силы и момент пары сил также не следует рассматривать как формальные величины, введенные для удобства доказательства. В технике очень часто проще задать не силу или пару, а их моменты. Например, в характеристику электродвигателя входит не сила, с которой статор действует на ротор, а вращающий момент.