Тема 4. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ЧАСТОТНЫМ КРИТЕРИЯМ УСТОЙЧИВОСТИ

1. Цель работы

Изучение методики оценки устойчивости линейных систем автоматического управления по критерию устойчивости А.В. Михайлова, получение практических навыков работы в применении этого критерия.

1. Содержание работы

1. Изучение теоретических основ построения частотных критериев устойчивости.
2. Анализ устойчивости системы по критерию А.В. Михайлова.
3. Получение результатов решения задачи в виде графика кривой Михайлова. Определение числа корней характеристического уравнения с положительной вещественной частью с помощью формулы А.В. Михайлова.
4. Выводы.

1. Теоретические основы работы

Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. Эти критерии являются графоаналитическими и получили широкое распространение, так как позволяют сравнительно легко исследовать устойчивость систем высокого порядка, а также имеют простую геометрическую интерпретацию и наглядность.

Наибольшее распространение среди частотных критериев устойчивости получил критерий Михайлова. Этот критерий устойчивости, сформулированный в 1938г. советским ученым А.В. Михайловым, является, по существу, геометрической интерпретацией принципа аргумента и позволяет судить об устойчивости системы на основании рассмотрения некоторой кривой, называемой кривой Михайлова.

Пусть функционирование - АС описывается линейным дифференциальным уравнением n-го порядка с постоянными вещественными коэффициентами:

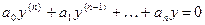. (4.1)

Его характеристическое уравнение имеет вид:

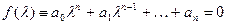. (4.2)

Критерий устойчивости Михайлова позволяет решить вопрос о расположении корней характеристического уравнения (4.2) на комплексной плоскости и, следовательно, решить вопрос об устойчивости нулевого решения (4.1).

Полагая 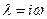, получим:

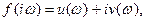
где

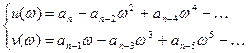(4.3)

Величину 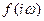при заданном значении параметра 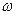можно изобразить в виде вектора на комплексной плоскости 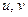с началом в точке 0.

При изменении 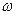в интервале 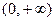, конец этого вектора опишет некоторую кривую, которая называется кривой Михайлова.

Теорема Михайлова. Для асимптотической устойчивости невозмущенного решения уравнения (3.12), характеристическое уравнение которого имеет вид (3.13) и не имеет чисто мнимых корней, необходимо и достаточно, чтобы вектор 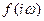, описывающий кривую Михайлова, повернулся на угол 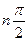, где n - степень многочлена (4.2).

Практически кривая Михайлова строится следующим образом:

1. Для уравнения n-го порядка составить характеристический многочлен .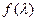

2. Составить характеристический комплекс 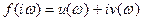, положив .

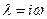3. Найти точки пересечения кривой Михайлова с осями и и w, для надо решить уравнения 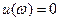и .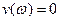

4. Для полного представления о поведении исследуемой кривой задать промежуточные значения 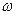, по формулам (4.3) вычислить 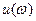и 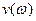, полученные точки соединить плавной кривой.

5. Найти результирующий угол поворота 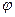вектора .

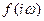6.По формуле 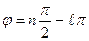определить значение 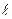- число корней в кривой положительной полуплоскости и сделать вывод об устойчивости системы.

1. Порядок выполнения работы

1. Изучить теоретическую часть работы.
2. Для представленного дифференциального уравнения, описывающего поведение системы автоматического регулирования (САР), составить характеристический многочлен вида (4.2).
3. Пользуясь геометрическим критерием устойчивости Михайлова, исследовать на устойчивость невозмущенное движение САР. Построить вид кривой Михайлова, найти число корней уравнения (4.2) с положительной вещественной частью.
4. Объяснить полученные результаты. Сделать выводы.

1. Варианты заданий

Исследовать на устойчивость по критерию Михайлова невозмущенное движение САР.

5.1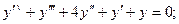

5.2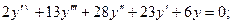

5.3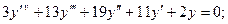

5.4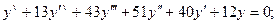

5.5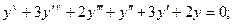

5.6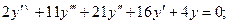

5.7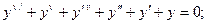

5.8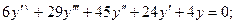

5.9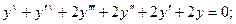

5.10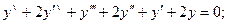

6. Содержание отчёта

1. Постановка задачи.

2. Порядок выполнения работы.

3. Краткая теория (общие определения устойчивости, критерий устойчивости Михайлова).

4. Алгоритм решения задачи.

5. Описание программы расчета. Листинг программы.

6. Результаты решения задачи (график кривой Михайлова, выводы).

7. Список используемой литературы.

Литература

1. Малкин И.Г. Теория устойчивости движения. - .М.: Наука, 1972. - 530с.

2. Меркин Д.Р. Введение в теорию устойчивости движения. - М.: Наука, 1981. – 312с.