Глава 1. Предварительные сведения
Реферат
Нильпотентные и метанильпотентные группы
Выполнил:
магистрант 1 курса 2 группы
направления 01.04.01 «Математика»
Максаков С.П.
Научный руководитель:
кандидат физико-математических наук, доцент Сорокина М.М.
Брянск 2016
СОДЕРЖАНИЕ
Введение …………………………………………………………………..………3
Глава 1. Предварительные сведения…………………………………………......5
1.1. Определения и обозначения, используемые в работе……………………...5
1.2. Используемые результаты…………………………………………………8
Глава 2. Нильпотентные группы…………………………………………….…12
2.1. Нильпотентные конечные группы их простейшие свойства………….....12
2.2. Критерии нильпотентности групп………………………………………....15
2.3. Метанильпотентные группы……………………………………………….18
Заключение…………………………………………………………………….....20
Список используемой литературы…………………………………………...…21
Введение
Понятие группы послужило во многих отношениях образцом при перестройке математики на рубеже 19-20 вв. Истоки понятия группы обнаруживаются во многих дисциплинах. Великому французскому математику Галуа принадлежат многие достижения в теории групп: открытие роли так называемых нормальных подгрупп, в связи с задачей о разрешимости уравнений в радикалах; установление свойства простоты знакопеременных групп степени 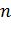 . Им был введен термин «группа» (le groupe), хотя строгого определения не было введено. Важную роль в систематизации и развитии теории групп сыграл трактат о группах подстановок другого великого французского ученого К. Жордана, опубликованный в 1870 году. А. Кэли явно пользовался термином «группа», систематически использовал таблицы умножения, ныне называемые таблицами Кэли, доказал представимость всякой конечной группы подстановками.
. Им был введен термин «группа» (le groupe), хотя строгого определения не было введено. Важную роль в систематизации и развитии теории групп сыграл трактат о группах подстановок другого великого французского ученого К. Жордана, опубликованный в 1870 году. А. Кэли явно пользовался термином «группа», систематически использовал таблицы умножения, ныне называемые таблицами Кэли, доказал представимость всякой конечной группы подстановками.
Еще один источник понятия группы - теория чисел. Л. Эйлер, начиная с 1761, изучая «вычеты, остающиеся при делении степеней», по существу пользовался сравнениями и разбиениями на классы вычетов, что на теоретико-групповом языке означает разложение группы на смежные классы по подгруппе. К. Гаусс в «Арифметических исследованиях» в 1801, занимаясь уравнением деления круга, определил подгруппы группы Галуа, а также, изучая «композицию двоичных квадратичных форм», доказывал, что классы эквивалентных форм образуют относительно композиции конечную абелеву группу.
Осознание в конце 19 века принципиального единства теоретико-групповых идей, существовавших к тому времени независимо в разных областях математики, привело к выработке современного абстрактного понятия групп. (С. Ли, Г. Фробениус и др.). Уже в 1895 году С. Ли определял группу как совокупность преобразований, замкнутую относительно их композиции. Изучение групп без предположения их конечности и без каких бы то ни было предположений о природе элементов впервые оформилось в самостоятельную область математики с выходом книги О. Ю. Шмидта «Абстрактная теория групп» в 1916 году.
Реферат имеет следующую структуру. В главе 1 приводятся некоторые предварительные сведения, используемые в работе. Основное содержание реферата представлено в главе 2. В ней рассматриваются нильпотентные и метанильпотентные группы, их примеры и свойства, изучаются критерии нильпотентности для групп, устанавливаются связи между нильпотентными группами и группами других классов. В основе проведенных исследований лежит монография [7].
Глава 1. Предварительные сведения
