Полный факторный эксперимент

При планировании по схеме полного факторного эксперимента реализуются все возможные комбинации факторов на всех выбран­ных для исследования уровнях. Необходимое количество опытов N при полном факторном эксперименте определяется по формуле N = р^к, где р — количество уровней, k — число факторов.

Если эксперименты проводятся на двух уровнях, то постановка опытов по такому плану называется иолным факторным экспериментом типа 2^к. Каждый фактор, участвующий в процессе, имеет определенный предел изменения своей величи­ны. Совокупность всех значений, которые принимает фактор, на­зывается областью определения фактора. Но в обла­сти определения надо найти локальную подобласть для планиро­вания эксперимента, т. е. для каждого фактора необходимо ука­зать тот интервал изменения параметров, в пределах которого про­водятся исследования. Для этого на основании априорной инфор­мации устанавливаются ориентировочно значения факторов, комбинации которых дают наилучший результат. Этой комбинации значений факторов соответствует многомерная точка в факторном пространстве, которая принимается за исходную при построении плана эксперимента. Координаты этой точки называются основными уровнями факторов.

После того как основной уровень выбран, переходим к следую­щему шагу — выбору интервалов варьирования. Интервалом варьированияфактора называется некоторое число, прибав­ления которого к основному уровню дает верхний, а вычитание — нижний уровень фактора.

Поскольку факторы изучаемого процесса неоднородны и имеют различные единицы измерения, их следует привести к единой системе исчисления путем перехода от действительных значении фак­торов к кодированным по формуле

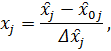
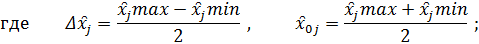
x_j – кодированное значение фактора;

x̑_j – натуральное значение фактора;

x̑_0j - натуральное значение фактора на основном уровне;

j – номер фактора;

𝛥x̑_j – интервал варьирования.

В безразмерной системе координат верхний уровень равен +1, нижний — соответственно —1, координаты основного уровня рав­ны нулю. Для случая N— 2² условия проведения эксперимента записываются в виде таблицы, которую называют матрицей планирования эксперимента (табл. 1). Строки соответ­ствуют различным опытам, столбцы — значениям факторов (еди­ницы для упрощения записи опущены).

Таблица 1

Матрица планирования 2²

Номер опыта	х0	х1	х2	у
	+ +	- +	- -
	+	-	+
	+	+	+

Построение матриц планирования основано на правиле чередо­вания знаков. В первом столбце они меняются поочередно, во вто­ром чередуются через два, в третьем — через четыре и т. д. по сте­пеням двойки. По результатам эксперимента определяются коэф­фициенты математической модели

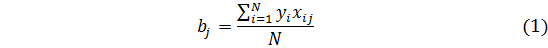
Чтобы провести процедуру вычисления коэффициента b₀ в со­ответствии с формулой (1), в матрицу планирования введен стол­бец фиктивной переменной х₀, которая во всех опытах принимает значение +1.

Коэффициенты при независимых переменных указывают на си­лу влияния факторов. Чем больше численная величина коэффици­ента bj, тем большее влияние оказывает фактор. Если коэффи­циент имеет знак « + », то с увеличением значения фактора у уве­личивается, а если «—», то уменьшается.

Планируя эксперимент, мы стремимся получить линейную мо­дель. Однако у нас нет уверенности в том, что в выбранных интер­валах варьирования процесс описывается линейной моделью. Один из часто встречающихся видов нелинейности связан с тем, что эффект (влияние) одного фактора зависит от уровня, на кото­ром находится другой фактор. Это означает, что имеет место эф­фект взаимодействия двух факторов. Полный факторный экспери­мент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, по­лучить столбец произведения двух факторов (табл. 2). Математи­ческая модель выглядит следующим образом

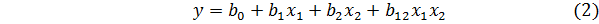
Таблица 2

Матрица планирования эксперимента 2² с эффектом взаимодействия

Номер опыта	х0	х1	х2	x1x2(x3)	y
	+ +	- +	- -	+ -	y1 y2
	+	-	+	-	y3
	+	+	+	+	y4

Коэффициент b₁₂ вычисляется аналогично по формуле (1).