Справочная информацця по технологии работы с режимом «Регрессия» надстройки Пакет анализа MS Excel
Режим работы «Регрессия» служит для расчета параметров уравнения линейной регрессии и проверки его адекватности исследуемому процессу.
Для решения задачи регрессионного анализа в MS Excel выберите в меню Сервис командуАнализ данных и инструмент анализа «Регрессия».
В появившемся диалоговом окне задаем следующие параметры:
1. Входной интервал Y – это диапазон данных по результативному признаку. Он должен состоять из одного столбца.
2. Входной интервал X – это диапазон ячеек, содержащих значения факторов (независимых переменных). Число входных диапазонов (столбцов) должно быть не больше 16.
3. Флажок Метки, установите в том случае, если в первой строке диапазона стоит заголовок.
4. Флажок Уровень надежности активизируется, если в поле, находящееся рядом с ним введете уровень надежности, отличный от установленного по умолчанию. Используется для проверки значимости коэффициента детерминации R2 и коэффициентов регрессии.
5. Константа ноль. Данный флажок установите, если линия регрессии должна пройти через начало координат (а0 = 0).
6. Выходной интервал/ Новый рабочий лист/ Новая рабочая книга – укажите адрес верхней левой ячейки выходного диапазона.
7. Флажкив группе Остатки установите, если необходимо включить в выходной диапазон соответствующие столбцы или графики.
8. Флажок График нормальной вероятности сделайте активным, если требуется вывести на лист точечный график зависимости наблюдаемых значений Y от автоматически формируемых интервалов персентилей.
После нажатия кнопки ОК в выходном диапазоне получите отчет.
Методические указания по проведению однофакторного корреляционного и регрессионного анализа
Задача
Некоторая фирма занимается поставками различных грузов на короткие расстояния внутри города. Оценить стоимость таких услуг, зависящую от затрачиваемого на поставку времени. В качестве наиболее важного фактора, влияющего на время поставки, выбрано пройденное расстояние. Исходные данные о десяти поставках приведены в табл. 5.5.
Таблица 5.5
Данные о времени поставок и пройденном расстоянии
| Расстояние, км | 3,5 | 2,4 | 4,9 | 4,2 | 3,0 | 1,3 | 1,0 | 3,0 | 1,5 | 4,1 |
| Время, мин |
Определите характер зависимости между расстоянием и затраченным временем, используя мастер диаграмм MS Еxcel, проанализируйте применимость метода наименьших квадратов, постройте уравнение регрессии, используя МНК, проанализируйте силу регрессионной связи. Проведите регрессионный анализ, используя режим работы «Регрессия» в MS Еxcel и сравните с результатами, полученными ранее. Посчитать и построить графически меру ошибки регрессионной модели, используя табличный процессор Excel.
Решение
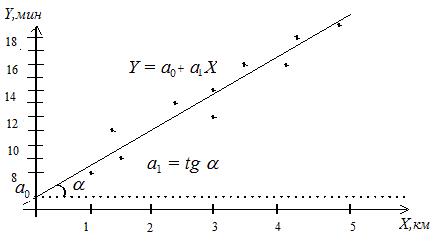
Рис. 5.3. График исходных данных и предполагаемая линия регрессии
На графике постройте исходные данные по десяти поездкам.
Помимо расстояния на время поставки влияют пробки на дорогах, время суток, дорожные работы, погода, квалификация водителя, вид транспорта. Построенные точки не находятся точно на линии, что обусловлено описанными выше факторами. Но эти точки собраны вокруг прямой линии, поэтому можно предположить линейную связь между параметрами. Все исходные точки равномерно распределены вдоль предполагаемой прямой линии, что позволяет применить метод наименьших квадратов.
Вычислите суммы, необходимые для расчета коэффициентов уравнения линейной регрессии и коэффициента детерминации R2 с помощью вспомогательной таблицы (табл. 5.6).
Таблица 5.6
Расчетная таблица
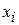 | 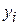 | 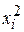 | 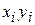 | 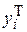 | 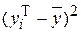 | 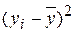 |
| 3,5 | 12,25 | 56,00 | 15,223 | 2,634129 | 5,76 | |
| 2,4 | 5,76 | 31,2 | 12,297 | 1,697809 | 0,36 | |
| 4,9 | 24,01 | 93,1 | 18,947 | 28,59041 | 29,16 | |
| 4,2 | 17,64 | 75,60 | 17,085 | 12,14523 | 19,36 | |
| 3,0 | 9,00 | 36,00 | 13,893 | 0,085849 | 2,56 | |
| 1,3 | 1,69 | 14,30 | 9,371 | 17,88444 | 6,76 | |
| 1,0 | 1,00 | 8,00 | 8,573 | 25,27073 | 31,36 | |
| 3,0 | 9,00 | 42,00 | 13,893 | 0,085849 | 0,16 | |
| 1,5 | 2,25 | 13,50 | 9,903 | 13,66781 | 21,16 | |
| 4,1 | 16,81 | 65,60 | 16,819 | 10,36196 | 5,76 | |
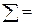 28,9 28,9 | 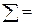 136 136 | 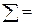 99,41 99,41 | 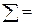 435,30 435,30 | – | 112,4242 | 122,4 |
Среднее значение y вычислите по формуле:
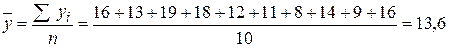 .
.
Вычислите коэффициенты линейной регрессии по формулам (5.8) и (5.9):
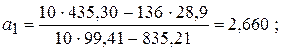
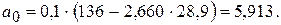
Таким образом, искомая регрессионная зависимость имеет вид:
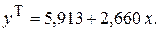
Наклон линии регрессии 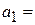 2,66 минут на км. – это количество минут, приходящееся на один км расстояния. Координата точки пересечения прямой с осью Y
2,66 минут на км. – это количество минут, приходящееся на один км расстояния. Координата точки пересечения прямой с осью Y 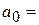 5,913 минут – это время, которое не зависит от пройденного расстояния, а обуславливается всеми остальными возможными факторами, явно не учтенными при анализе.
5,913 минут – это время, которое не зависит от пройденного расстояния, а обуславливается всеми остальными возможными факторами, явно не учтенными при анализе.
Вычислите коэффициент детерминации:
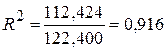 или 91,8 %.
или 91,8 %.
Проведите регрессионный анализ с использованием режима Регрессия MS Excel. Значения параметров, установленных в одноименном диалоговом окне, представлены на рис. 5.4.
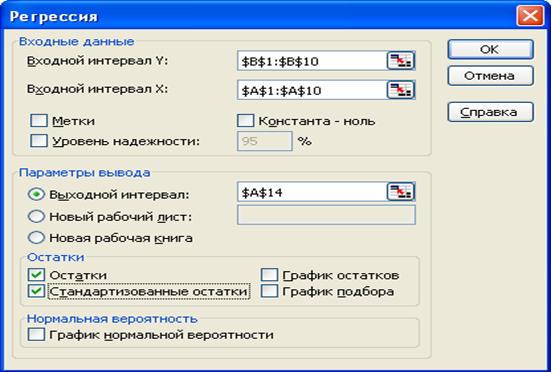
Рис. 5.4 Окно входных данных
Сгенерируются результаты по регрессионной статистике, представленные в таблице 5.7.
Таблица 5.7
Вывод итогов
| Регрессионная статистика | |
| Множественный R | 0,958275757 |
| R-квадрат | 0,918292427 |
| Нормированный R-квадрат | 0,90807898 |
| Стандартная ошибка | 1,11809028 |
| Наблюдения |
Рассмотрите представленную в таблице 5.7 регрессионную статистику.
Величина R-квадрат, называемая также мерой определенности, характеризует качество полученной регрессионной прямой. Это качество выражается степенью соответствия между исходными данными и регрессионной моделью (расчетными данными). Мера определенности всегда находится в пределах интервала [0; 1]. Мера определенности равная 0,91829 говорит об очень хорошей подгонке регрессионной прямой к исходным данным и совпадает с коэффициентом детерминации R2, вычисленным по формуле.
Таким образом, линейная модель объясняет 91,8 % вариации времени доставки, что означает правильность выбора фактора (расстояния). Не объясняется 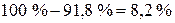 вариации времени поездки, которые обусловлены остальными факторами, влияющими на время поставки, но не включенными в линейную модель регрессии.
вариации времени поездки, которые обусловлены остальными факторами, влияющими на время поставки, но не включенными в линейную модель регрессии.
Рассчитанный уровень значимости αр = 1,26E-05 < 0,05 (показатель значимость F в таблице Дисперсионный анализ подтверждает значимость R2.
Множественный R – коэффициент множественной корреляции R – выражает степень зависимости независимых переменных (X) и зависимой переменной (Y) и равен квадратному корню из коэффициента детерминации, эта величина принимает значения в интервале от нуля до единицы. В простом линейном регрессионном анализе множественный R равен коэффициенту корреляции Пирсона. Действительно, множественный R в нашем случае равен коэффициенту корреляции Пирсона (0,95827), который вычисляется по формуле:

Теперь рассмотрите среднюю часть расчетов, представленную в таблице 5.8 (приведена в сокращенном варианте). Здесь даны коэффициент регрессии а1 (2,65970168) и смещение по оси ординат, то есть константа a0 (5,913462144).
Таблица 5.8
Результаты регрессионального анализа
| Коэффициенты | Стандартная ошибка | t-статистика | P-значение | |
| Y-пересечение | 5,913462144 | 0,884389599 | 6,686489927 | 0,00015485 |
| Переменная X | 2,65970168 | 0,280497238 | 9,482095791 | 1,26072E-05 |
Исходя из расчетов, запишите уравнение регрессии таким образом:
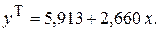
Это уравнение, совпадает с уравнением, полученным при расчете по МНК вручную с точностью до ошибки округления.
Направление связи между переменными определяется на основании знаков (отрицательный или положительный) коэффициента регрессии (коэффициента а1). Знак коэффициента регрессии положительный (+2,660), следовательно, связь также является положительной.
Далее проверьте значимость коэффициентов регрессии: а0 и а1. Сравните попарно значения столбцов Коэффициенты и Стандартная ошибка в таблице 5.8, видно, что абсолютные значения коэффициентов больше чем их стандартные ошибки. К тому же эти коэффициенты являются значимыми, о чем можно судить по значениям показателя
Р-значение в таблице 5.8, которые меньше заданного уровня значимости α = 0,05.
В таблице 5.9 представлены результаты вывода остатков. При помощи этой части отчета определите отклонения каждой точки от построенной линии регрессии. Наибольшее абсолютное значение остатка – 1,89256, наименьшее – 0,05399. Для лучшей интерпретации этих данных воспользуйтесь графиком исходных данных и построенной линией регрессии, представленными на рис. 5.5. Как видно, линия регрессии хорошо «подогнана» под значения исходных данных.
Таблица 5.9
Результаты анализа остатков
| Вывод остатка | |||
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 15,22241803 | 0,777581975 | 0,737641894 | |
| 12,29674618 | 0,703253823 | 0,667131568 | |
| 18,94600038 | 0,053999622 | 0,051225961 | |
| 17,0842092 | 0,915790799 | 0,868751695 | |
| 13,89256718 | – 1,892567185 | –1,795356486 | |
| 9,371074328 | 1,628925672 | 1,545256778 | |
| 8,573163824 | –0,573163824 | – 0,543723571 | |
| 13,89256718 | 0,107432815 | 0,101914586 | |
| 9,903014664 | – 0,903014664 | – 0,8566318 | |
| 16,81823903 | – 0,818239033 | – 0,776210624 |
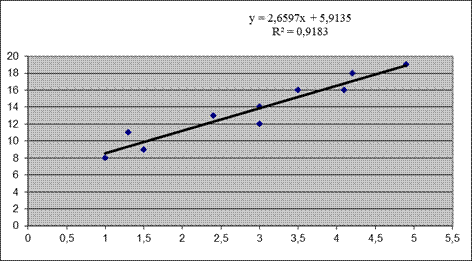
Рис. 5.5. Исходные данные и линия регрессии
Приблизительным, но самым простым и наглядным способом проверки удовлетворительности регрессионной модели является графическое представление отклонений.
Отложите отклонения  по оси Y, для каждого значения
по оси Y, для каждого значения 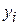 . Если регрессионная модель близка к реальной зависимости, то отклонения будут носить случайный характер и их сумма будет близка к нулю. В рассмотренном примере
. Если регрессионная модель близка к реальной зависимости, то отклонения будут носить случайный характер и их сумма будет близка к нулю. В рассмотренном примере 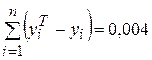 .
.
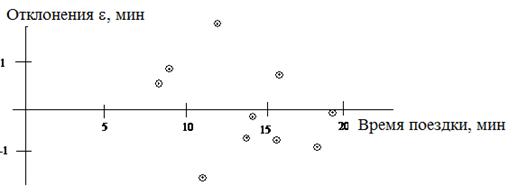
Рис. 5.6. График отклонений
Таким образом, в результате использования регрессионного анализа в табличном процессоре MS Excel:
· построили уравнение регрессии;
· установили форму зависимости и направление связи между переменными – положительная линейная регрессия, которая выражается в равномерном росте функции;
· установили направление связи между переменными;
· оценили качество полученной регрессионной прямой;
· смогли увидеть отклонения расчетных данных от данных исходного набора.
Порядок выполнения работы
1. Ознакомьтесь с методикой проведения корреляционного и регрессионного анализа в Excel.
2. У преподавателя получите вариант индивидуального задания.
3. Парную выборку опытных данных 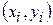 нанесите на график и визуально оцените применимость линейного уравнения регрессии.
нанесите на график и визуально оцените применимость линейного уравнения регрессии.
4. Вычислите коэффициенты прямой линейной регрессий и коэффициент корреляции.
5. На график опытных точек нанесите рассчитанную линию прямой линейной регрессии. Визуально оцените близость уравнения регрессии к функциональной связи.
6. Сделайте выводы по работе и оформить отчет.
Оформление отчета
Отчет о лабораторной работе должен содержать:
1) постановку задачи;
2) результаты вычислений индивидуальных заданий;
3) анализ полученных результатов табличном процессоре MS Excel.
Варианты индивидуальных заданий
Постройте регрессионную модель (линейную) для исходных данных, приведенных в таблице 5.10.
Таблица 5.10
Индивидуальные задания
| Номера контрольных задач | ||||||||||||||||||||||||
| i | ||||||||||||||||||||||||
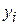 |  | 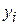 |  | 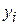 |  | 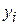 |  | 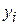 |  | |||||||||||||||
| 2,62 | 0,90 | 15,57 | 75,53 | – 44,2 | 5,85 | 45,11 | 43,20 | 93,53 | 30,76 | |||||||||||||||
| 2,44 | 0,71 | 15,41 | 75,38 | – 44,6 | 5,70 | 44,90 | 43,03 | 93,37 | 30,59 | |||||||||||||||
| 2,25 | 0,56 | 15,22 | 75,20 | – 44,7 | 5,52 | 44,75 | 42,86 | 93,16 | 30,43 | |||||||||||||||
| 2,06 | 0,38 | 15,03 | 74,04 | – 44,8 | 5,36 | 44,56 | 42,72 | 92,99 | 30,29 | |||||||||||||||
| 1,89 | 0,21 | 14,85 | 74,87 | – 45,0 | 5,19 | 44,38 | 42,54 | 92,81 | 30,10 | |||||||||||||||
| 1,71 | 0,06 | 14,68 | 74,71 | – 45,2 | 5,03 | 44,20 | 42,38 | 92,63 | 29,94 | |||||||||||||||
| 1,53 | – 0,11 | 14,50 | 74,53 | – 45,4 | 4,86 | 44,02 | 42,21 | 92,45 | 29,77 | |||||||||||||||
| 1,40 | – 0,13 | 14,36 | 74,52 | – 45,5 | 4,84 | 43,89 | 42,19 | 92,32 | 29,75 | |||||||||||||||
| 1,26 | – 0,14 | 14,23 | 74,51 | – 45,6 | 4,83 | 43,75 | 42,18 | 92,18 | 29,74 | |||||||||||||||
| 1,13 | – 0,16 | 14,11 | 74,48 | – 45,8 | 4,81 | 43,62 | 42,16 | 92,05 | 29,72 | |||||||||||||||
| 1,00 | – 0,18 | 13,97 | 74,47 | – 45,9 | 4,79 | 43,49 | 42,14 | 91,92 | 29,70 | |||||||||||||||
| 0,86 | – 0,19 | 13,83 | 74,46 | – 46,0 | 4,78 | 43,35 | 42,13 | 91,78 | 29,69 | |||||||||||||||
| 0,73 | – 0,21 | 13,70 | 74,44 | – 46,2 | 4,76 | 43,22 | 42,11 | 91,65 | 29,67 | |||||||||||||||
| 0,62 | – 0,15 | 13,59 | 74,50 | – 46,3 | 4,82 | 43,11 | 42,17 | 91,54 | 29,73 | |||||||||||||||
| Номера контрольных задач | ||||||||||||||||||||||||
| i | ||||||||||||||||||||||||
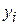 |  | 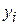 |  | 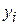 |  | 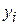 |  | 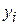 |  | |||||||||||||||
| – 17,9 | – 69,9 | 173,2 | 80,9 | 14,6 | 11,8 | 27,2 | 7,6 | – 10,2 | 51,5 | |||||||||||||||
| – 18,0 | – 70,0 | 179,5 | 81,8 | 14,4 | 11,6 | 20,3 | 7,2 | – 10,4 | 51,4 | |||||||||||||||
| – 18,2 | – 70,1 | 185,8 | 82,6 | 14,3 | 11,4 | 13,4 | 6,8 | – 10,6 | 51,2 | |||||||||||||||
| – 18,5 | – 70,3 | 176,1 | 87,4 | 14,1 | 11,2 | 16,5 | 13,4 | – 10,9 | 51,0 | |||||||||||||||
| – 18,7 | – 70,5 | 179,0 | 93,9 | 13,9 | 11,0 | 19,7 | 20,1 | – 11,1 | 50,9 | |||||||||||||||
| – 18,9 | – 70,6 | 180,0 | 86,7 | 13,7 | 10,9 | 20,8 | 12,3 | – 11,3 | 50,7 | |||||||||||||||
| – 19,0 | – 70,8 | 181,1 | 79,5 | 13,5 | 10,7 | 21,9 | 4,5 | – 11,4 | 50,5 | |||||||||||||||
| – 19,2 | – 70,9 | 180,0 | 79,8 | 13,4 | 10,6 | 20,2 | 4,6 | – 11,6 | 50,4 | |||||||||||||||
| – 19,3 | – 71,0 | 178,9 | 80,1 | 13,3 | 10,5 | 18,7 | 4,7 | – 11,7 | 50,3 | |||||||||||||||
| – 19,4 | – 71,1 | 181,0 | 86,9 | 13,1 | 10,4 | 20,9 | 12,5 | – 11,8 | 50,1 | |||||||||||||||
| – 19,6 | – 71,2 | 183,2 | 93,8 | 13,0 | 10,2 | 23,0 | 20,2 | – 12,0 | 49,9 | |||||||||||||||
| – 19,7 | – 71,4 | 181,0 | 89,3 | 12,9 | 10,0 | 21,1 | 14,9 | – 12,1 | 49,7 | |||||||||||||||
| – 19,8 | – 71,4 | 178,9 | 84,8 | 12,7 | 9,9 | 19,0 | 9,9 | – 12,2 | 49,5 | |||||||||||||||
| – 20,0 | – 71,5 | 183,5 | 87,5 | 12,6 | 9,7 | 23,9 | 12,0 | – 12,4 | 49,4 | |||||||||||||||
Окончание табл. 5.10
| Номера контрольных задач | ||||||||||
| i | ||||||||||
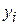 |  | 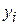 |  | 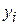 |  | 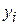 |  | 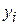 |  | |
| 12,9 | 62,9 | 17,2 | 80,7 | – 14,6 | 11,9 | 26,2 | – 7,6 | 10,2 | 61,5 | |
| 13,0 | 63,0 | 17,5 | 81,6 | – 14,4 | 11,7 | 19,3 | – 7,2 | 10,4 | 61,4 | |
| 13,2 | 63,1 | 18,8 | 82,4 | – 14,3 | 11,5 | 12,4 | – 6,8 | 10,6 | 61,2 | |
| 13,5 | 63,3 | 17,1 | 87,2 | – 14,1 | 11,3 | 15,5 | – 13,4 | 10,9 | 61,0 | |
| 13,7 | 63,5 | 17,0 | 93,7 | – 13,9 | 11,1 | 18,7 | – 20,1 | 11,1 | 60,9 | |
| 13,9 | 63,6 | 18,0 | 86,5 | – 13,7 | 10,9 | 19,8 | – 12,3 | 11,3 | 60,7 | |
| 14,0 | 63,8 | 18,1 | 79,3 | – 13,5 | 10,8 | 20,9 | – 4,5 | 11,4 | 60,5 | |
| 14,2 | 63,9 | 18,0 | 79,6 | – 13,4 | 10,7 | 19,2 | – 4,6 | 11,6 | 60,4 | |
| 14,3 | 64,0 | 17,9 | 80,0 | – 13,3 | 10,5 | 17,7 | – 4,7 | 11,7 | 60,3 | |
| 14,4 | 64,1 | 18,0 | 86,7 | – 13,1 | 10,4 | 19,9 | – 12,5 | 11,8 | 60,1 | |
| 14,6 | 64,2 | 18,2 | 93,6 | – 13,0 | 10,2 | 22,0 | – 20,2 | 12,0 | 59,9 | |
| 14,7 | 64,4 | 18,0 | 89,1 | – 12,9 | 10,0 | 20,1 | – 14,9 | 12,1 | 59,7 | |
| 14,8 | 64,4 | 17,9 | 84,6 | – 12,7 | 9,9 | 18,0 | – 9,9 | 12,2 | 59,5 | |
| 15,0 | 64,5 | 18,5 | 87,3 | – 12,6 | 9,7 | 22,9 | – 12,0 | 12,4 | 59,4 |
Контрольные вопросы
1. Какие основные задачи решают с помощью корреляционного и регрессионного анализа?
2. Сформулируйте принцип Лежандра.
3. Какими показателями измеряется теснота корреляционной связи?
4. В чем отличие стохастической связи от функциональной?
5. В чем состоит значение уравнения регрессии? Что характеризуют коэффициенты регрессии?
6. Для чего нужен коэффициент корреляции? В каких пределах он изменяется?
7. Как осуществляется проверка значимости коэффициентов регрессии?
8. Как проверить адекватность уравнения в целом?
9. В каких случаях применяется модель множественной регрессии?
10. Как проводится корреляционный и регрессионный анализ в MS Excel?
