Интеграл как функция верхнего предела.

Теорема 4.1.Пусть Рассмотрим функцию имеет место равенство

Доказательство. Функция 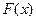существует, так как . Имеем

, где точка ; если , а , по непрерывности. Теорема доказана.

Таким образом, для непрерывной функции 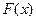- первообразная для .

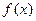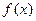Теорема 4.2. Пусть - любая первообразная для на 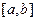. Тогда

если .

Доказательство. В условиях теоремы, для некоторой константы 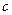, где

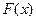определена как в предыдущей теореме. Имеем, далее,

Теорема доказана.

Эта теорема позволяет вычислять определённые интегралы через значения первообразных ( и тем самым в некотором смысле оправдывает введение понятия первообразной). Можно слегка обобщить её.

Теорема 4.3. Пусть , исключая конечное число точек внутри отрезка.

Тогда , где функция 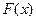в точках разрыва определена произвольно, а между ними – как первообразная для 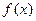на соответствующем промежутке.

Ни уточнять, ни доказывать мы её не будем.

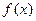Теорема 4.4. (Вторая теорема о среднем). Пусть функция , а на

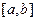монотонна. Тогда , такая, что .

Лемма 4.3.1.(Формулы Бонне) .Если на 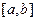функция 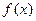не возрастает и неотрицательна, а , то , для которой

.

Аналогично, если на 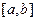и не убывает, а , то такая, что

. , где .

Доказательство. Докажем первую часть. Разобьём отрезок на более мелкие точками .Имеем :

Вторая сумма будет стремиться к 0 при мелкости разбиения стремящейся к 0, потому что второй сомножитель под интегралом ограничен ,а первый – это колебание функции 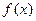на , и сумма будет стремиться к нулю, так как .

Значит, первая сумма будет стремиться к интегралу. Положим . Имеем:

.

Функция , следовательно, поскольку все разности неотрицательны, , и , где . В силу непрерывности , , , что даёт первую из формул. Вторая доказывается аналогично.

Доказательство теоремы. Пусть 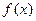монотонно убывает. В первой формуле Бонне возьмём вместо 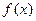разность . После преобразований (формальных и не связанных с новыми идеями) получим утверждение теоремы.

Примечание. Эта теорема в лекционном курсе не доказывалась.

Несобственные интегралы. Введение.

5.1 Рассмотрим интеграл . Геометрически он представляет площадь , ограниченную осью Ох, прямыми х=1 и х=а и кривой . Рассмотрим . Этот предел называется несобственным интегралом первого рода от функции на промежутке и обозначается .

Определение 5.1. Пусть функция . Если существует , то он называется несобственным интегралом первого рода и обозначается .

Определение 5.2.Пусть функция и существует . Он называется несобственным интегралом второго рода и обозначается 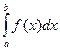.(Бесконечность может быть любого знака).

Отметим, что это, несмотря на обозначение, не обычный интеграл, потому что подинтегральная функция стремится к бесконечности в точке .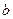

Реально встречаются несобственные интегралы, которые имеют особенности и первого и второго рода одновременно. Их изучение сводится к тому, что пространство интегрирования разбивается на промежутки, в каждом из которых содержится не более одной особенности (то есть, либо единственная точка, где функция не ограничена, либо в одно из концов).

Легко проверить, что подстановка вида превращает интеграл первого рода в интеграл второго рода, а подстановка - интеграл второго рода в интеграл первого рода. Будем по этой причине рассматривать интегралы первого рода, а для интегралов второго рода только приводить результаты.

Если несобственный интеграл существует, говорят, что он сходится, в противном случае – расходится.

Теорема 5.1. Сходящиеся на несобственные интегралы образуют линейное пространство.

Доказательство является следствием того обстоятельства, что функции, имеющие предел в точке, образуют линейное пространство

( ).

Теорема 5.2.(Критерий Коши) Для того, чтобы несобственный интеграл первого рода

сходился, необходимо и достаточно, чтобы .

Доказательство. Это критерий Коши для функции при .

Определение 5.3. Говорят, что несобственный интеграл сходится абсолютно, если сходится интеграл (для интегралов второго рода пределы нужно изменить соответственно).

Если несобственный интеграл сходится, но не абсолютно, говорят, что он сходится условно.

Теорема 5.3. Абсолютно сходящийся интеграл сходится.

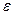Доказательство. Рассмотрим функцию и .Этот предел будет существовать, если выполнен критерий Коши, т.е., если по произвольному найдётся , такое, что для всех будет выполняться неравенство . Переходя к интегралам, получим . По условию, по тому же можно подобрать , такое, что для любых будет выполняться неравенство (по тому же критерию Коши) .Возьмём ; согласно неравенству , тогда будет выполняться и нужное нам неравенство. Значит, по критерию Коши будет сходиться и исходный интеграл .Теорема доказана.

Признаки сходимости

6.1. Интегралы от знакопостоянных функций.

Мы будем предполагать, что .Случай с неположительной функцией исследуется аналогично. Заметим также, что будет монотонно возрастающей функцией.

Теорема 6.1.1. Если ограничена сверху, интеграл сходится.

Доказательство. Монотонно возрастающая ограниченная функция имеет предел.

Теорема 6.1.2. Если, начиная с некоторого , , то из сходимости

следует сходимость , а из расходимости - расходимость

.

Доказательство следует из того, что если интеграл сходится, то он ограничен, значит, ограничен и меньший интеграл.

Теорема 6.1.3. Если , начиная с некоторого , , то интегралы

сходятся или расходятся одновременно.

Доказательство. Прямое следствие неравенств и предыдущей теоремы.

В задачах в качестве одной из функций 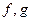часто употребляется .

Теорема 6.1.4. сходится при ; интеграл сходится при .

Доказательство. Эти интегралы берутся, достаточно рассмотреть пределы.

6.2. Интегралы от знакопеременных функций.

Имеют место следующие два признака сходимости (условной) .

Теорема 6.2.1 .(Признак Абеля) Рассмотрим интеграл . Если интеграл

сходится, а функция 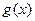монотонна и ограничена на , то указанный интеграл сходится.

Теорема 6.2.2. (Признак Дирихле) Интеграл сходится, если , а монотонно при .

На самом деле, признак Абеля следует из признака Дирихле.

Докажем признак Дирихле. По критерию Коши, достаточно показать, что

для достаточно больших .По второй теореме о среднем,

.

Множители могут быть сделаны сколь угодно малыми, поскольку,

по условию, , а модули интегралов . Теорема доказана.