Тема 4.Частотные характеристики систем САУ

Частотные характеристики САУ характеризуют реакцию систем на синусоидальное входное воздействие в установившемся режиме.

К частотным характеристикам относятся:

АФЧХ - амплитудно-фазовая частотная характеристика;

АЧХ – амплитудно-частотная характеристика;

ФЧХ – фазовая частотная характеристика;

ЛАЧХ – логарифмическая АЧХ;

ЛФЧХ – логарифмическая ФЧХ.

АФЧХ представляет собой частотную передаточную функцию W(jω), которая получается путем замены в передаточной функции W(p) оператора Лапласа p на комплексную переменную jω. АФЧХ представляет собой вектор на комплексной плоскости в полярных координатах Н(ω) и φ(ω), которые являются соответственно АЧХ и ФЧХ:

W(jω) = Н(ω)∙е^jφ(ω) = N(ω) + jM(ω). (1)

Здесь: Н(ω) – АЧХ, которая представляет собой зависимость значения модуля вектора АФЧХ от круговой частоты;

φ(ω) – ФЧХ, которая представляет собой зависимость аргумента вектора АФЧХ от круговой частоты;

N(ω) = Н(ω)∙cosφ(ω) – проекция вектора АФЧХ на действительную ось комплексной плоскости;

M(ω) = Н(ω)∙sinφ(ω) – проекция вектора АФЧХ на мнимую ось комплексной плоскости;

При изменении частоты ω от нуля до бесконечности АФЧХ представляет собой кривую в комплексной плоскости, называемую годографом.

Рассмотрим частотные характеристики отдельных типовых звеньев.

Апериодическоезвено.

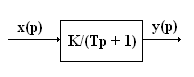
Основные формулы и соотношения

W(jω) = K/(1 + jωT) = = .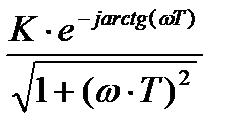

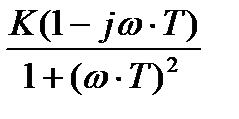Н(ω) = 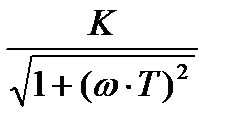; φ(ω) = – arctg(ωT);

N(ω) = K/[1 + (ω∙T)²]; M(ω) = – K∙ ω∙T/[1 + (ω∙T)²]. (2)

φ(0) = 0^o; Н(0) = K; N(0) = K; M(0) = 0;

φ(ω = 1/T) = – 45^o; Н(T) = K/√2; N(T) = K/2; M(T) = – K/2;

φ(ω → ∞) = – 90^o; Н(∞) = N(∞) = M(∞) = 0.

Интегрирующее звено.

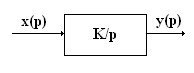
Основные формулы и соотношения

W(jω) = K/jω = K∙e 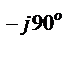/ω;

Н(ω) = K/ω; φ(ω) = – 90^o;

N(ω) = 0; M(ω) = – K/ω; (3)

φ(0) = – 90^o; Н(0) = ∞; N(0) = 0; M(0) = – ∞;

φ(ω → ∞) = – 90^o; Н(∞) = N(∞) = M(∞) = 0.

Колебательное звено.

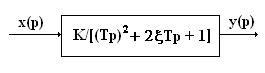
Основные формулы и соотношения

W(jω) = K/[– (ω∙T)² + j2ξ∙T∙ω + 1] = =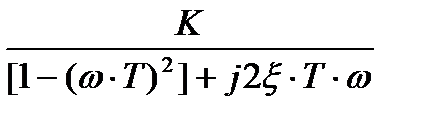

= = ;

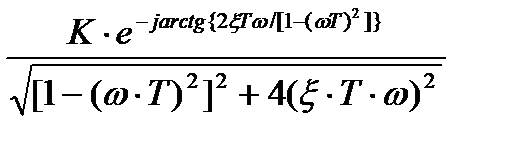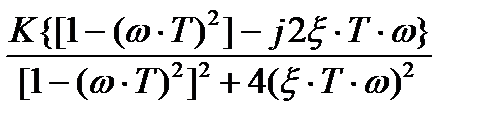Н(ω) = 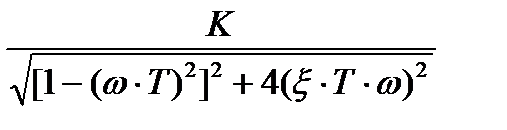; φ(ω) = – arctg{2ξ∙T∙ω/[1– (ω∙T)²]};

N(ω) = K∙[1 – (ω∙T)²]/{[1– (ω∙T)²]² + 4(ξ∙T∙ω)²};

M(ω) = – 2K∙ξ∙T∙ω/{[1– (ω∙T)²]² + 4(ξ∙T∙ω)²}; (4)

φ(0) = 0^o; Н(0) = K; N(0) = K; M(0) = 0;

φ(ω) = 1/T) = – 90^o; Н(T) = K/(2ξ); N(T) = 0; M(T) = – K/(2ξ);

φ(ω → ∞) = – 180^o; Н(∞) = N(∞) = M(∞) = 0.

Идеальное дифференцирующее звено.

Основные формулы и соотношения

W(jω) = jK∙ω = K∙ω∙e ;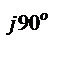

Н(ω) = K∙ω; φ(ω) = 90^o;

N(ω) = 0; M(ω) = K∙ω; (5)

φ(0) = 90^o; Н(0) = 0; N(0) = 0; M(0) = 0;

φ(ω → ∞) = 90^o; Н(∞) = M(∞) = ∞; N(∞) = 0.

Кроме перечисленных ранее частотных характеристик при анализе свойств САУ широко используются логарифмические частотные характеристики, к которым относятся:

ЛАЧХ – логарифмическая амплитудно-частотная характеристика;

ЛФЧХ – логарифмическая фазовая частотная характеристика.

ЛАЧХ представляет собой график зависимости L(ω) = 20lg[H(ω)] от десятичного логарифма частоты lg(ω). При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе, а по оси ординат L(ω). Единицей L(ω) является децибел (дБ), равный одной десятой Бела. L(ω) = 20 означает, что на данной частоте при прохождении сигнала через звено его амплитуда увеличивается в 10 раз.

ЛФЧХ – это график зависимости частотной функцииφ(ω) от десятичного логарифма частоты lg(ω). При его построении по оси абсцисс откладывают частоту в логарифмическом масштабе, по оси ординат откладывают φ(ω) в градусах или радианах.

В обоих случаях за единицу масштаба по оси абсцисс принимается декада – это частотный интервал, соответствующий изменению частоты в 10 раз. Ось ординат при построении этих характеристик проводят часто через точку (ω = 1) которая соответствует началу координат lg(1) = 0.

На практике часто кривую линию ЛАЧХ заменяют приближенным графиком, состоящим из нескольких пересекающихся прямых отрезков (асимптот), к которым стремится логарифмическая функция при определенных значениях частот, называемых сопрягающими частотами.

Рассмотрим аналитические выражения для ЛАЧХ и правила построения асимптотических ЛАЧХ для ряда характерных типовых звеньев.

Апериодическое звено. Формула ЛАЧХ согласно (2) принимает следующий вид:

L(ω) = 20lg[H(ω)] = 20lgК - 20lg 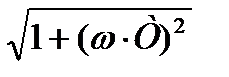. (6)

В области низких частот ω<ω_c = 1/T, меньших по значению, чем сопрягающая частота ω_c, L(ω) = 20lgК. В этой области частот кривая ЛАЧХ заменяется прямой линией, параллельной оси абсцисс и проходящей на уровне 20lgК.

В области высоких частот ω>ω_cL(ω) = 20lgК - 20lg(ω∙Т). В этой области частот кривая ЛАЧХ заменяется прямой линией, имеющей наклон минус 20 дБ на декаду.

Обе прямые или иначе асимптоты пересекаются в точке, соответствующей сопрягающей частоте ω_c = 1/T.

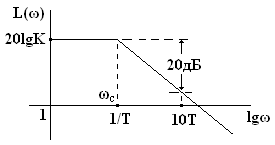
Интегрирующее звено. Формула ЛАЧХ согласно (3) принимает следующий вид:

L(ω) = 20lg[H(ω)] = 20lgК - 20lgω. (7)

Так как при частоте ω = 1 согласно выражению (7) функция L(ω) = 20lgК, то естественно асимптота в виде прямой линии с отрицательным наклоном в 20 дБ должна проходить через эту точку при ω = ω_c = 1.

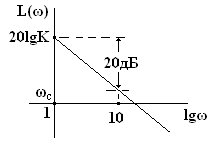
Колебательное звено. Формула ЛАЧХ согласно (4) принимает следующий вид:

L(ω) = 20lg[H(ω)] = 20lgK – 20lg 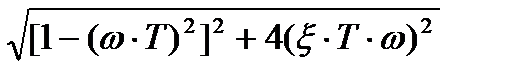. (8)

В области низких частот ω<ω_c = 1/T, меньших по значению, чем сопрягающая частота ω_c, L(ω) = 20lgК, а при значениях частоты ω>ω_c можно под корнем пренебречь единицей и слагаемым 4(ξ∙ω∙T)². В результате получаем уравнение асимптотической ЛАЧХ:

L(ω) = 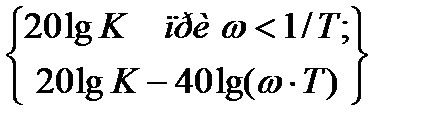. (9)

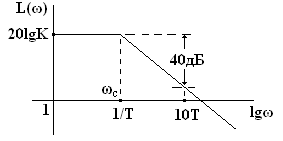
Согласно уравнению (9) асимптотическая ЛАЧХ при ω<ω_c = 1/T, где ω_c – сопрягающая частота, параллельна оси частот, а при ω_c имеет минус 40 децибел на декаду.

Идеальное дифференцирующее звено. Формула ЛАЧХ согласно (5) принимает следующий вид:

L(ω) = 20lg[H(ω)] = 20lgК + 20lgω. (10)

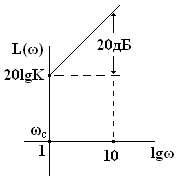
По аналогии с интегрирующим звеном асимптотическая ЛАЧХ представляет собой прямую, проходящую через точку 20lgK при ω_c = 1 с наклоном плюс 20дб/дек.

После того, как мы познакомились с частотными характеристиками САУ и правилами их построения, можно вернуться к рассмотрению других частотных критериев устойчивости систем САУ.

Частотный критерий Найквиста. Данный критерий предложен в 1932 году американским ученым Г. Найквистом и позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутой системы. Для того, чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы ее АФЧХ W(jω) при разомкнутой цепи обратной связи не охватывала в комплексной плоскости точку с координатами (- 1; j0).

Если разомкнутая система статическая (не имеет интегрирующих звеньев), то при ω = 0 ее АФЧХ начинается на вещественной оси в точке N(0) = H(0) = K, где К – коэффициент усиления разомкнутой системы. Заканчивается АФЧХ приω = ∞ вначале координат.

Если система является астатической (имеет интегрирующие звенья), то ее АФЧХ начинается при ω = 0 в бесконечности, поскольку в знаменателе функции W(jω) имеется множитель (jω)^r, где r – порядок астатизма. Соответственно, при r = 1 и ω = 0 характеристика W(jω) уходит в бесконечность вдоль отрицательной мнимой полуоси, при r = 2 – вдоль отрицательной действительной полуоси, а при r = 3 – вдоль положительной мнимой полуоси.

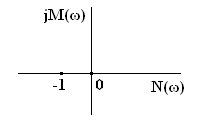
Логарифмический критерий Найквиста. Для оценки устойчивости САУ по данному критерию используются графики ЛАЧХ и ЛФЧХ разомкнутой системы САУ. Система САУ считается устойчивой, если при φ(ω) = - 180^о кривая ЛАЧХ находится в отрицательной области: L(ω) = 20lg[H(ω)] < 0, т.е. ЛАЧХ должна пересечь ось абсцисс раньше, чем фаза, спадая, перейдет за значение -180^о. Систему САУ можно считать также устойчивой, если на частоте среза ω_ср, на которой L(ω_ср) = 20lg[H(ω_ср)] = 0, значение аргумента φ(ω_ср) > - 180^o.

При оценке устойчивости САУ необходимо определить запас устойчивости, т.е. степень удаленности системы от границы устойчивости. В качестве меры запаса устойчивости используется запас устойчивости по амплитуде h(ω) и запас устойчивости по фазе ψ(ω_ср).

Запас устойчивости САУ по амплитуде h(ω) определяется на частоте ω_у, при которой φ(ω_у) = - 180^о: h(ω_у) = - L(ω_у) и показывает допустимое увеличение ЛАЧХ , при котором система окажется на грани устойчивости. Запас по амплитуде представляет собой запас по коэффициенту усиления К разомкнутой системы по отношению его к критическому по устойчивости значению.

Запас устойчивости по фазе ψ(ω_ср) определяется на частоте среза ω_ср, как: ψ(ω_ср) = φ(ω_ср) + 180^о и показывает, на какую величину должно возрасти запаздывание по фазе в системе на частоте среза ω_ср, чтобы система оказалась на грани устойчивости.

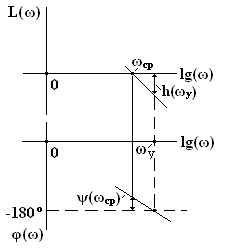
При проектировании САУ рекомендуется выбирать ψ(ω_ср) ≥ 30^о, а h(ω_у) ≥ 6 дБ, что соответствует примерно двойному запасу коэффициента усиления К по устойчивости.