Тест Математика 8 класс. Конкурс «Ребус»

1. В трех кучках лежат соответственно 12, 24 и 19 спичек. За ход можно переложить спичку из одной кучки в другую. За какое наименьшее число ходов можно получить три кучки с 8, 21 и 26 спичками?

А. 5;

Б. 4;

В. 7;

Г. 9.

2. Выполните деление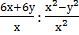

А. ;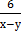

Б. ;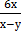

В. ;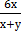

Г. .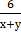

3. В параллелограмме ABCD диагональ AC, равная 24см, образует со стороной AD угол в 30⁰, О – точка пересечения диагоналей AC и BD, OE _┴ AD. Найдите длину отрезка OE

А. 8 см;

Б. 5см;

В. 3см;

Г. 6 см.

4. В конкурсе участвовали 5 человек. На каждый вопрос один из них дал неправильный ответ, остальные — правильный. Число правильных ответов у Пети равно 10 — меньше, чем у любого другого. Число правильных ответов у Васи равно 13 — больше, чем у любого другого. Сколько всего вопросов было в конкурсе?

А. 14;

Б. 13;

В. 12;

Г. 15.

5. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 143⁰. Найдите величину угла АВС. Ответ дайте в градусах.

А. 102;

Б. 100;

В. 106;

Г. 99.

6. Найдите координаты точек пересечения параболы у = х² + 10х - 11 с осью ординат

А. (0;-11);

Б. Нет точек пересечения;

В. (11;0);

Г. (-11;0).

7. Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?

А. 46;

Б. 56;

В. 40;

Г. 50.

8. На часах половина девятого. Чему равен угол в градусах между часовой и минутной стрелками?

А. 75;

Б. 90;

В. 270;

Г. 30.

9. Петя хотел нарисовать правильный треугольник ABC. Но, поскольку он рисовал неточно, получился треугольник с углами ∠A = 59◦ и ∠B = 63◦ . Потом Петя провёл высоты CE и BD, но, поскольку угольник был слегка перекошен, получил углы ∠ADB = ∠AEC = 92◦ . Найдите градусную меру угла AED.

А. 59;

Б. 61;

В. 58;

Г. 74.

10. Вася задумал два числа. Их сумма равна произведению и равна их частному. Какие числа задумал Вася?

А. 2; -5,3;

Б. 4; 2,5;

В. 0, 5; -1;

Г. -1;2,5.

11. Расстояние от точки пересечения диагоналей прямоугольника до его смежных сторон равно 2,6 см и 3,9 см. Вычисли периметр прямоугольника.

А. 6,5;

Б. 13;

В. 26;

Г. 14.

12. Бригада должна была выполнить заказ за 10 дней. Ежедневно перевыполняя норму на 27 деталей, бригада за 7 дней работы не только выполнила задание, но еще изготовила дополнительно 54 детали. Сколько деталей в день изготовляла бригада?

А. 72;

Б. 71;

В. 69;

Г. 54.

13. В классе больше 20, но меньше 30 учеников. При этом в классе тех, кто ходит в шахматный кружок, в 2 раза меньше, чем тех, кто не ходит. А тех, кто ходит в шашечный кружок, в 3разаменьше, чем тех, кто не ходит. Сколько учеников в классе?

А. 26;

Б. 23;

В. 24;

Г. 29.

14. Таня и Ваня ели арбуз. Таня съела половину трети от четверти арбуза, а Ваня – четверть половины от трети арбуза. Кто съел больше арбуза?

А. Таня;

Б. Ваня;

В. Поровну;

Г. Нет верного ответа.

15. График линейной функции пересекает ось координат в точках (2; 0) и (0; -5). Задайте эту функцию формулой.

А. у = - 2,5х – 5;

Б. у=5х – 5;

В. у=2х – 5,5;

Г. у=2,5х – 5.