Виды интегральных уравнений

Рассмотрим некоторые частные случаи одномерных уравнений, которые, с одной стороны, важны в практических приложениях и, с другой стороны, наиболее изучены.

Уравнения, в которые искомая функция входит линейно, называются линейными интегральными уравнениями. Одним из них является уравнение Фредгольма первого рода

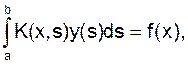
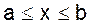
Уравнение Фредгольма второго рода имеет вид

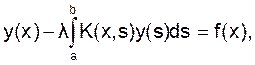
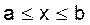
В уравнениях Фредгольма ядро 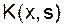определено и ограничено на квадрате 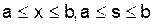. Если K(x,s) = 0 при s>х, т. е. ядро отлично от нуля только на треугольнике 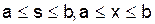, то уравнения и переходят в уравнения Вольтерра соответственно первого и второго рода:

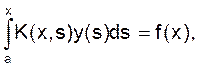
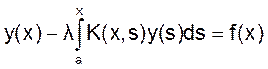
Мы будем рассматривать задачи для уравнений второго рода. Задачи для уравнений первого рода являются некорректно поставленными. Их рассмотрение выходит за рамки данного краткого курса. Заметим лишь, что для решения некорректных задач, т. е. уравнений или, могут быть использованы методы регуляризации.

Если правая часть уравнения равна нулю, то получается однородное уравнение Фредгольма второго рода, которое можно записать в виде

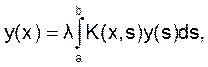
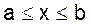
Это уравнение допускает нулевое (тривиальное) решение у(х) = 0. Для него может быть поставлена задача на собственные значения. Параметры х_i, при которых уравнение имеет отличные от нуля решения 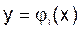, называются собственными значениями ядра K(x,s) или уравнения, а отвечающие им решения 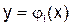- собственными функциями.

Теорема Фредгольма. Если 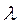не является собственным значением ядра К(х,s), то неоднородное уравнение имеет единственное непрерывное решение у(х) при 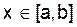, в противном случае данное неоднородное уравнение или не имеет решений, или имеет их бесчисленное множество.

В практических приложениях важную роль играют уравнения Фредгольма второго рода с вещественным симметричным ядром K(x,s), т. е. когда

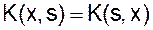
Симметричное ядро обладает следующими свойствами:

1) симметричное ядро имеет хотя бы одно собственное значение;

2) все собственные значения симметричного ядра действительны;

3) собственные функции 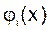симметричного ядра ортогональны, т.е.

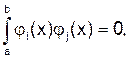
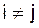
Уравнение Вольтерра не имеет собственных значений. Соответствующее однородное уравнение, т. е. при f(x) = 0, имеет только тривиальное решение у(х) = 0. Следовательно, неоднородное уравнение всегда при любом значении 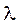имеет решение, и при том единственное.

Итак, основными задачами для рассматриваемых интегральных уравнений являются:

1) нахождение решения неоднородного интегрального уравнения при заданном значении параметра ;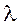

2) вычисление собственных значений и отыскание соответствующих им собственных функций однородного интегрального уравнения.

Методы решения.

Численные методы. Эти методы называют также квадратурными. Они основаны на использовании формул численного интегрирования для вычисления определенных интегралов, входящих в интегральные уравнения. Численные методы получили особенно широкое распространение в связи с внедрением компьютеров, хотя эти методы можно использовать и в ручном счете при небольшом числе узлов. Численные методы могут применяться для решения как линейных, так и нелинейных интегральных уравнений.

Рассмотрим нелинейное интегральное уравнение вида

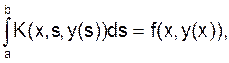
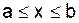
Разобьем отрезок [а,b] на части точками x_i = а + ih (i = 0,1,... ,n).

Заменим интеграл в уравнении некоторой квадратурной формулой

с помощью значений сеточной функции u_i в узлах:

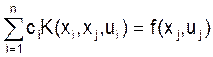j=1, 2, …, n.

где c_i — коэффициенты квадратурной формулы численного интегрирования.

Мы получили систему нелинейных алгебраических уравнений. Решая систему, получаем значения сеточной функции в выбранных узлах отрезка [а,b]. Для практического решения этой системы можно использовать рассмотренные ранее методы, например метод Ньютона Вопрос о сходимости сеточного решения u_i к значениям искомой функции y(x_i) при 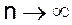может быть рассмотрен лишь для конкретного вида интегрального уравнения. В общем случае сходимость численного метода исследовать трудно.

Рассмотрим линейные интегральные уравнения. Запишем сеточное выражение для однородного уравнения Фредгольма:

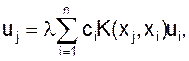
или:

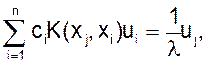j=1, 2, …,n

Система линейных уравнений в таком виде описывает задачу на собственные значения матрицы А, элементами которой являются числа а_j,i=c_iK(x_j,x_i). Матрица А имеет n собственных значений (с учетом кратности), которые являются приближениями к собственным значениям однородного уравнения Фредгольма.

В случае неоднородного уравнения Фредгольма вместо однородной системы получим следующую систему линейных алгебраических уравнений:

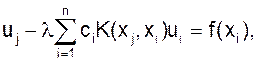j=1, 2, …,n

Эта система уравнений может быть решена одним из рассмотренных ранее методов, например методом Гаусса. В соответствии с теоремой Фредгольма параметр λ не должен быть равен ни одному из собственных значений. Если он попадает в окрестность некоторого собственного значения, то система становится плохо обусловленной, и сеточное решение u_i может сильно отличаться от искомых значений y(x_i).

На практике обычно собственные значения интегрального уравнения неизвестны, поэтому ограничиваются исследованием практической сходимости. Оно состоит в проведении серии расчетов со сгущающейся сеткой. Если при этом наблюдается сходимость сеточных значений, то в качестве искомого решения принимаются результаты последнего расчета на густой сетке. При решении уравнения Вольтерра система линейных алгебраических уравнений имеет треугольный вид, и она легко решается последовательным нахождением значений u_i (по аналогии с обратным ходом метода Гаусса).

Рассмотренный подход можно использовать и для решения многомерных интегральных уравнений. При этом в многомерной расчетной области значительно возрастает число узлов. Для решения таких задач требуется большой объем памяти компьютера; системы уравнений в этих случаях более целесообразно решать итерационными методами.

Примеры задач.

Пример 1.1 (реализация в пакете MATLAB).

Найти в пакете MATLAB решение интегрального уравнения Фредгольма:

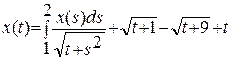
Решение:

function z=Q_Fredholm(t,s)

z=1/sqrt(t+s^2);

function z=F_Fredholm(t)

z=sqrt(t+1)-sqrt(t+9)+t;

function [X,Y]=Solve_Fredholm(a1,b1,N,Lambda)

% задание временной сетки

h=(b1-a1)/(N-1); i=1:N; t(i)=a1+h*(i-1);

s=t;

%задание коэффициентов квадратурной формулы методом трапеций

A(1)=0.5;

m=2:N-1;

A(m)=1; A(N)=0.5;

%вычисление значений функции Q(t,s) в узлах сетки

for i=1:N

for j=1:N

q(i,j)=Q_Fredholm(t(i),s(j));

end;

end;

%вычисление значений функции f(t)в узлах временной сетки

F=F_Fredholm(t);

for i=1:N

for j=1:N

if i==j

M(i,j)=1-Lambda*A(i)*q(i,j)*h;

else

M(i,j)=-Lambda*A(i)*q(i,j)*h;

end;

end;

end;

%нахождение решения интегрального уравнения

X=t;

Y=M^-1*F';

Результаты:

>> a1=1;

>> b1=2;

>> N=300;

>> Lambda=1;

>> [X,Y]= Solve_Fredholm (a1,b1,N,Lambda);

>> plot(X,Y)

Получим следующий график:

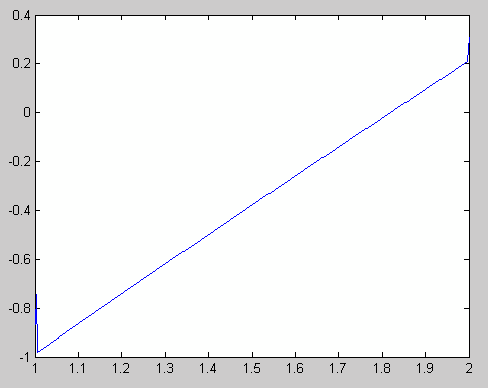
Пример 1.2.

Найти в пакете MATLAB решение интегрального уравнения Вольтерра:

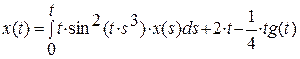
Решение:

function z=Q_Voltaire(t,s)

z=t*sin(t*s^3)^2;

function z=F_Voltaire(t)

z=2*t-1/4*tan(t);

function [T,Y]=Solve_Voltaire(t1,t2,N)

% задание временной сетки

h=(t2-t1)/(N-1);

i=1:N;

t(i)=t1+h*(i-1);

s=t;

%задание коэффициентов квадратурной формулы методом трапеций

A(1)=0.5;

m=2:N-1;

A(m)=1;

A(N)=0.5;

%вычисление значений функции Q(t,s) в узлах сетки

for i=1:N

for j=1:N

q(i,j)=Q_Voltaire(t(i),s(j));

end;

end;

%вычисление значений функции f(t)в узлах временной сетки

F=F_Voltaire(t);

%вычисление решения интегрального уравнения

x(1)=F(1)/(1-A(1)*q(1,1));

for m=2:N

S=0;

for j=1:m-1

S=S+h*A(j)*q(m,j)*x(j);

end;

x(m)=F(m)+S./(1-h.*A(m).*q(m,m));

end;

T=t;

Y=x;

Результаты:

>> t1=0;

>> t2=5;

>> N=300;

>> [X Y]=Solve_Voltaire(t1,t2,N);

>> plot(X, Y)

Получим следующий график:

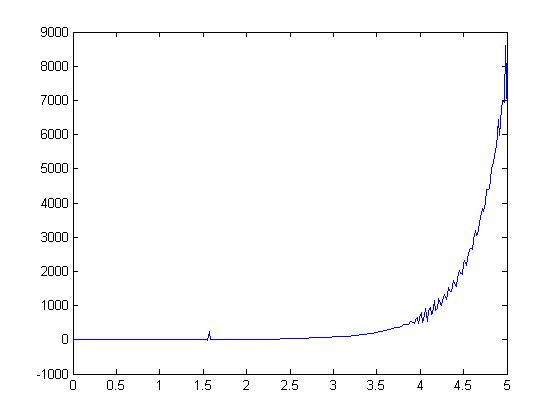
Пример 2(реализация в пакете MATCAD).

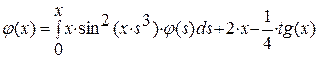1.Решение уравнения вида

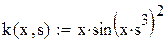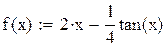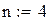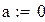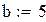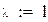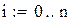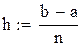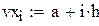1. Формирования весовых коэффициентов.

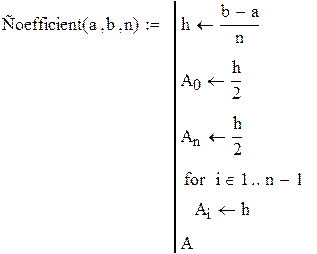2. Формирование матрицы коэффициентов для уравнения Фредгольма, Вольтерра.

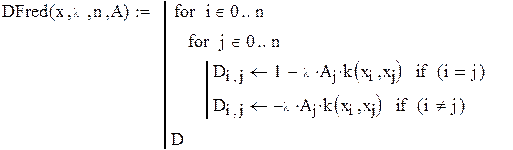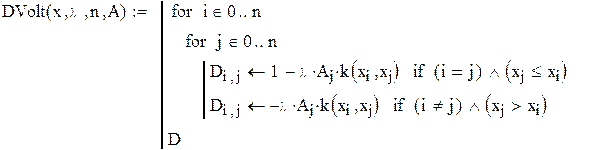3. Вычисление значений f(х)(правой части уравнения) в узловых точках.

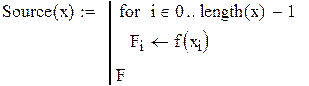Значения источника в узловых точках:

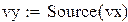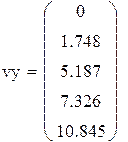Вычисляем значения искомой функции в узловых точках: ϕ(vx(i))

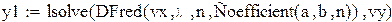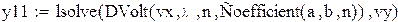Искомую функцию ϕ(х) запишем в виде :

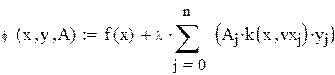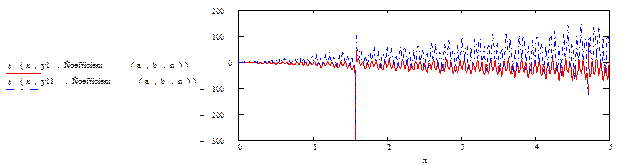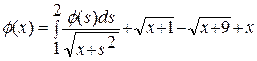2.Решение уравнения вида

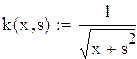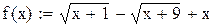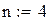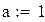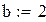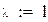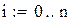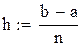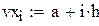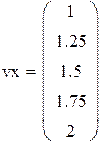Значения источника в узловых точках:

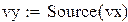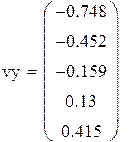Вычисляем значения искомой функции в узловых точках: ϕ(vx(i))

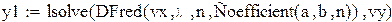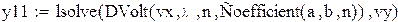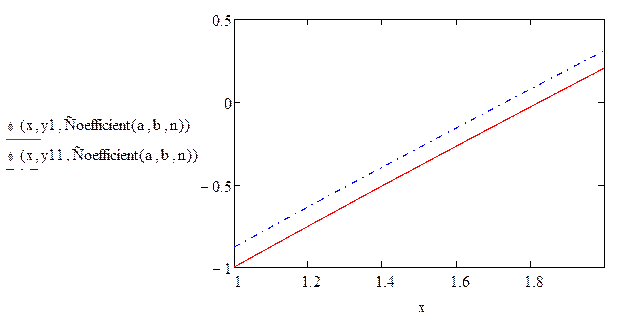
Искомую функцию ϕ(х) запишем в виде :
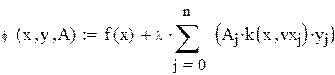