Выражения с переменной

Программа предусматривает изучение выражений с переменнойдвух видов:

- содержащих одну переменную вида: а + 22, 43 – b;

- содержащих две переменные вида: а + b, а - b, с • d, с : d . В основных требованиях программы сказано: учащиеся должны уметь находить числовые значения буквенных выражений при заданных чис­ловых значениях входящих в него букв. Этому умению естественно пред­шествует умение читать и записывать соответствующие выражения. Отсюда вытекают задачи, стоящие перед учителем при изучении выражений с переменной. При изучении таких выражений у детей необходимо сформировать умения:

- читать и записывать соответствующие выражения;

- находить числовое значение выражения при заданных числовых значениях входящих в него букв.

Решение этих задач теснейшим образом связано с понятием переменной. Термин «переменная» в курсе математики начальных классов практически не употребляется, однако работа по формированию этого понятия проводится в течение длительного времени, начиная с темы «Числа 1-10». Уже здесь выполняются упражнения на подбор чисел и заполнение пустых мест в соответствующих таблицах или отдельных квадратиках (окошечках). Например:

1) 7 = 5 + 2) 10 3) 10

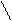
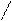
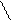
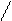
4) 7 = 6 + + -

5)

Слагаемое
Слагаемое
Сумма

В дальнейшем вводится и буквенное значение переменной. Это происходит в теме «Сложение и вычитание в пределах 100» при знакомстве с выражениями с одной переменной.

Вариант работы при этом может быть таким.

Рассматривается ряд числовых выражений, аналогичных тем, кото­рые будут вводиться. Например: 5 + 3; 1 + 3; 21 +3; 82 + 3.

Выясняется, что это за выражения, как они читаются, что можно о них рассказать (это суммы двух чисел; второе слагаемое у всех одно и то же - 3; первое слагаемое – разные числа). Сообщается, что в математике числа обозначают буквами. В этих выраже­ниях второе слагаемое везде равно 3, а вот первое - разные числа. Чтобы не перечислять все вторые слагаемые, обозначим их буквой а. Все эти выражения можно записать так: а + 3.

Предлагается детям прочитать полученное выражение (сумма чисел а и 3). Объясняется, что числа 5, 1, 21, 82 – это числовые значения буквы а. Следует провести разговор с детьми о том, какие значения еще может принимать буква а, и подвести к выводу, что а может принимать любые значения, то есть фактически устанавливается область определе­ния выражения. Этот вопрос очень важен при рассмотрении выражений вида 43 - b, а в дальнейшем и вида: а - b, а: b.

Усвоению буквенной символики помогают следующие упражнения:

1. Нахождение числовых значений буквенных выражений при заданных значения букв. Например: Вычислить значение выражения а + 7, если а = 8; 10;

а = 8; 8 + 7 = 15.

а = 10; 10 + 7 = 17.

При формировании умения вычислять числовое значение выражений при заданных числовых значениях входящих в них букв, необходимо обратить внимание детей на ход рассуждений и оформление записи.

2. Подбор самими учащимися числовых значений букв, входящих в выражение, и нахождение числовых значений этих выражений. Например, заполните таблицу:

m
n
m – n

Далее раскрывается понятие постоянной. Рассматриваются выражения, в которых постоянная величина фиксируется с помощью цифр: а ±1 2, 8 ± с. Здесь, как и на предыдущем этапе, предусматриваются упражнения на переход от числовых выражений к выражениям, записанным с помощью букв и цифр, и обратно. Используется пособие.

		15 + 8
		3 + 8
		40 + 8
m		m + 8
I слагаемое	II слагаемое	Сумма

Аналогично можно получить выражения: 17 ± n, k ± 30, а позднее 7 · b, а : 8, 48 : d.

Упражнения: 1. Запишите сумму чисел b и 20. Вычислите значения выражения, если

b = 5, b = 35, b = 20; 2. Прочитайте выражение d – 13. Придайте букве d два числовых значения и вычислите значения разности.

3. Преобразовать таблицу с тремя графами в таблицу с двумя графами и обратно:

b
d
b+d

d
28 + d

Важно обращать внимание на то, какие значения можно придавать букве в заданном выражении. Например, рассматривая выражение25 – k, надо придать букве значения и найти значение выражения. Можно ли придать букве другие значения? Какие? Любые ли значения можно придать букве? Делается вывод: букве k можно придавать любые числовые значения от 0 до 25.

Буквенные выражения используются также и в качестве средства обобщения формируемых у них знаний. Конкретной базой для использования буквенной символики как средства обобщения служат знания об арифметических действиях. Например, при рассмотрении частных случаев ум­ножения с числами 0 и 1:

1 • b = b; а • 1 = а;

0 • с = 0; b • 0 = 0.

Упражнения:

1. Записать при помощи букв свойства арифметических действий: a + b = b + a,

a b = b • a, …

2. Заменить сумму a + a + a + a произведением.

3. Выполните тождественное преобразование выражений (5 + b) • 3.

4. Доказать справедливость равенств или неравенств: с + 5 = 5 + с, с + 17 > с + 15,

с • 0 = 0, с • 1 = с.

Использование буквенной символики способствует повышению уровня обобщения знаний, готовит учащихся к изучению систематического курса алгебры в следующих классах.