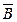Свойства операций над множествами. Практическая работа № 1
Практическая работа № 1
Дисциплина: Элементы математической логики
Тема: Решение задач на выполнение теоретико-множественных операций и на применение формулы мощности объединения нескольких конечных множеств
Цель занятия: научиться использовать аппарат теории множеств для решения задач.
Содержание отчета: тема, цель работы, номер вариант, для каждой задачи условие, решение, снабженное необходимыми формулами и выкладками, ответ.
Норма времени: 2 часа
Методическое обеспечение: методические указания к практической работе
Литература: Спирина, М.С. Дискретная математика: Учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. – М.: Издательский центр «Академия», 2004. – С. 60-61.
Методические указания
Под множеством понимается совокупность различных объектов, удовлетворяющих какому-то характеристическому свойству. Объекты, составляющие множество, называются элементами. Тот факт, что объект x принадлежит множеству A, передается записью x 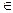 A (читается – «элемент x принадлежит множеству A»).. Если x не является элементом A, то пишут x
A (читается – «элемент x принадлежит множеству A»).. Если x не является элементом A, то пишут x 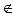 A. Элементы множеств обычно обозначаются строчными латинскими буквами x, y, a, b, c ; множества часто обозначают прописными латинскими буквами A, B, C, X, Y.
A. Элементы множеств обычно обозначаются строчными латинскими буквами x, y, a, b, c ; множества часто обозначают прописными латинскими буквами A, B, C, X, Y.
Способы задания множеств:
1. Перечислением своих элементов. A={a,b,c,...}.
2. Через описание ограничительного свойства. A={x| P(x)} – A множество таких элементов x, которые обладают свойством P(x).
Если множество содержит конечное число элементов, то говорят, что оно конечно,в противном случае множество называется бесконечным. Число элементов конечного множества A называется мощностьюмножества A и обозначается |A|. Если множество не содержит ни одного элемента, удовлетворяющего характеристическому свойству, оно называется пустым множеством и обозначается 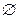 .
.
Множество B называется подмножеством множества A, если всякий элемент множества B является элементом множества A. Запись B 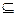 A ( не исключает, что B=A).
A ( не исключает, что B=A).
Пустое множество по определению является подмножеством любого множества. По определению пустое множество является конечным. По определению множество является подмножеством самого себя, A 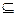 A.
A.
Если все рассматриваемые в ходе рассуждений множества являются подмножествами некоторого фиксированного множество U, то это множество называют универсальным (для рассматриваемого набора множеств) множеством или универсом
Множество всех подмножеств множества А называется булеаном этого множества и обозначается как 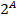 .
.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
| № | Операция | Графическое представление | Определение |
| Объединение множеств (теоретико-множественное сложение) | 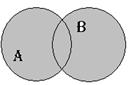 | А 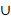 В={x|x В={x|x 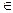 A или x A или x 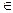 B} B} | |
| Пересечение множеств (теоретико-множественное умножение) |  | А 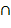 В={x| x В={x| x 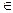 A и x A и x 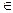 B} B} | |
| Разность множеств | 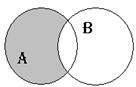 | А\В={x|x 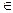 A, но x A, но x 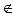 B} B} | |
| Дополнение множества | 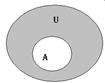 | 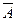 =U\A =U\A 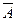 ={x| x ={x| x 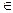 U, но x U, но x 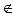 A} A} | |
| Симметрическая разность множеств | 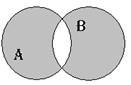 | А 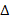 В=(A\B) В=(A\B) 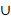 (B\A) А (B\A) А 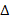 В=(A В=(A 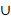 B) \ (А B) \ (А 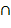 В) В) |
Свойства операций над множествами
1. Коммутативность.
относительно операции объединения, относительно операции пересечения.
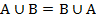 А
А 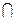 В=В
В=В 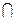 А
А
2. Ассоциативность.
относительно операции объединения, относительно операции пересечения.
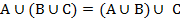 А
А 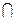 (В
(В 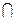 С)=(А
С)=(А 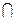 В)
В) 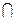 С
С
3. Дистрибутивность.
пересечения относительно объединения, объединения относительно пересечения.
А 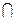 (В
(В 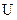 С)=( А
С)=( А 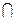 В)
В) 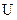 (А
(А 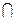 С)
С) 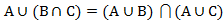
4. Закон де Моргана.
относительно объединения, относительно пересечения.
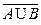 =
=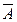
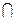
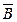

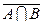 =
=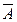
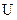
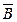

5.Законы поглощения
относительно объединения, относительно пересечения.
A 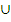 (A
(A 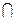 B)=A A
B)=A A 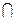 (A
(A 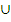 B)=A
B)=A
A 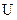 (
(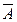
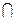 В )= А
В )= А 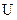 В A
В A 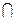 (
(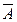
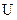 B)= А
B)= А 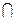 В
В
6. A 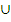 A=A A
A=A A 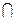 A=A
A=A
7. A 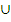
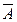 =J A
=J A 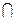
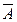 =
= 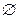
8. A 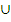
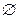 =A A
=A A 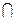 U=A
U=A
9.  A
A 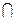
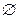 =
= 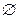
10. Закон двойного отрицания
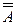 =A
=A
11. A\B = A