Теорема Поста о функциональной полноте
Обозначим через T -множество всех функций, сохраняющих константу 1, F-множество всех функций, сохраняющих константу 0, L -множество всех линейных функций, M -множество всех монотонных функций, S - множество всех самодвойственных функций. Нетрудно показать, что все перечисленные множества функций образуют замкнутые классы.
Теорема Поста о функциональной полноте.
Для того, чтобы система функций была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из следующих замкнутых классов T, F, L, Mи S.
Доказательство необходимости очевидно, так как если все функции системы принадлежат одному из классов, то замкнутость этого класса нарушает условия полноты.
Достаточность доказывается на основании следующих лемм.
Лемма 1.
Если функция не самодвойственна, то из неё путем подстановки функций xи 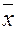 можно получить константу.
можно получить константу.
Доказательство.
Так как 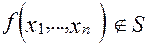 ,то найдется такой n-мерный набор
,то найдется такой n-мерный набор 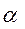 ,что
,что 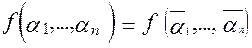 .
.
Рассмотрим функции 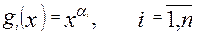 .
.
Пусть 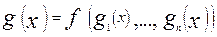 .Тогда
.Тогда 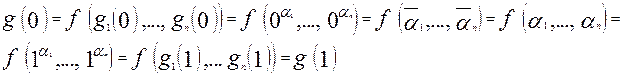 Мы получили
Мы получили 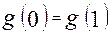 , т.е. функция
, т.е. функция 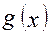 -константа.
-константа.
Лемма доказана.
Лемма 2.
Если функция не монотонна, то из неё, путем подстановки констант 0,1и функции x,можно получить функцию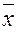 .
.
Доказательство.
Два одинаково размерных двоичных набора называются соседнимипо координате i, если наборы совпадают по всем другим координатам, а i -ая координата i в одном наборе равна 1, а в другом 0.
Так как функция не монотонна, то найдутся два таких набора 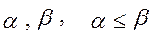 ,что
,что 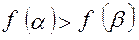 .
.
Очевидно, что среди таких наборов найдутся и соседние, и пусть они являются соседними по координате i. Рассмотрим функцию 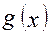 =
= 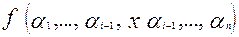 .
.
Мы имеем: 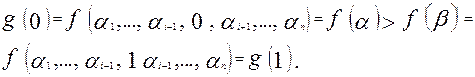
Отсюда следует доказательство леммы, так как 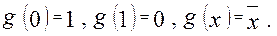
Лемма 3.
Если функция не линейная, то из неё путем подстановки констант 0, 1и функций x и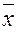 , можно получить функцию x&y.
, можно получить функцию x&y.
Доказательство.
Для заданной нелинейной функции построим полином Жегалкина P.Он нелинеен, т.е. найдется член, содержащий конъюнкцию не менее двух переменных. Не уменьшая общности будем предполагать, что этими переменными являются переменные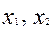 .Тогда полином Жегалкина для исходной нелинейной функции можно представить в виде:
.Тогда полином Жегалкина для исходной нелинейной функции можно представить в виде:
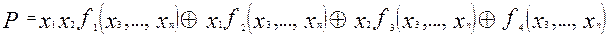 Здесь
Здесь 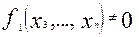 , т.е. найдется хотя бы один набор, на котором значение этой функции не равно 0. Мы имеем
, т.е. найдется хотя бы один набор, на котором значение этой функции не равно 0. Мы имеем 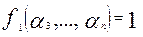 . Тогда
. Тогда 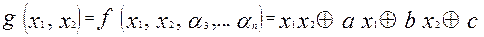 .
.
Рассмотрим функцию 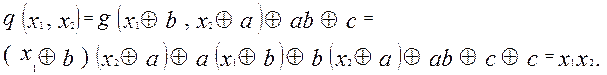 Лемма доказана.
Лемма доказана.
Пусть система функций целиком не принадлежит ни одному из классов T, F, L, M, S. Пусть t, f, l, m, s - функции из заданной системы, не принадлежащие соответственным классам (некоторые из них и даже все могут совпадать) и зависящие от тех же самых переменных.
Используя лемму 1, при помощи функции t, fи sможно получить константы 0и 1.
При помощи констант 0 и 1и функции m, используя лемму 2 можно получить 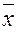 .
.
При помощи констант 0 и 1, функции 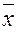 и функции l, используя лемму 3 можно получить функцию x &y.
и функции l, используя лемму 3 можно получить функцию x &y.
Получили систему функций, содержащую отрицание и конъюнкцию, тем самым доказали теорему.
