Задача № 5.6. Определить расстояние между двумя параллельными прямыми m и n
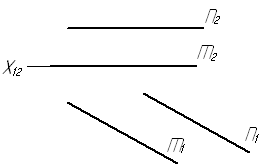
Рис. 30
Перпендикуляр, опущенный из любой точки одной прямой на другую, определяет расстояние между прямыми.
Обе параллельные прямые m и n параллельны плоскости П1. Зададим точку А на прямой m и опустим из этой точки А перпендикуляр на прямую n. Заменим плоскость П2 на плоскость П4 так, чтобы она была перпендикулярна к прямой n. Новая ось Х14 проведена перпендикулярно к проекции n1 прямой n. На линиях связи от новой оси Х14 откладываем отрезки, равные расстояниям от заменяемых проекций А2 и n2, точки А и прямой n, до оси Х12.
Получим проекцию А4 точки А и проекцию n 4 прямой n.
Расстояние между А4 и n 4 и будет искомым.
Задача № 5.7. Определить расстояние от точки А до плоскости
a(m ççn)^П2
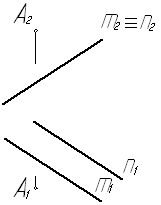
Рис. 31
Плоскость a (m ççn)является фронтально проецирующей. Перпендикуляр, опущенный из точки А на плоскость a, параллелен плоскости проекций П2 и длина проекции его отрезка на этой плоскости проекций П2 равна искомому расстоянию.
Задача № 5.8. Определить расстояние между двумя параллельными плоскостямиa (а ççb) и β (с Ça), a Ùβ ^П2.
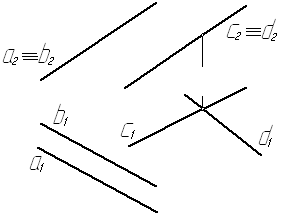
Рис. 32
Решение этой задачи можно свести к определению расстояния от точки К, взятой в плоскости a до другой плоскости β. См. решение задачи № 5.7.
Задача № 5.9. Определить угол между пересекающимися прямыми l и m.
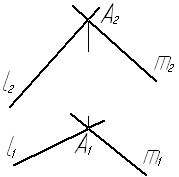
Рис. 33
Отмечаем в плоскости a(l Ç m) горизонталь h и поворачиваем плоскость вокруг горизонтали h в положение горизонтальной плоскости. При этом точки 1 и 2, принадлежащие горизонтали, остаются неподвижными. Точка А перемещается по окружности, плоскость которой перпендикулярна к горизонтали. На плоскость П1 окружность проецируется в отрезок прямой, перпендикулярной к горизонтальной проекции h1 горизонтали h. Проводим через горизонтальную проекцию А1 точки А прямую, перпендикулярную к h1, и отмечаем точку О1, в которой она пересекает h1. Точка О1 - горизонтальная проекция центра О окружности, по которой перемещается точка А. Его фронтальная проекция О2 принадлежит h2. Отрезки О1A1 и О2А2 - горизонтальная и фронтальная проекции радиуса RA указанной окружности.
Находим длину радиуса RA, для чего строим дополнительную ортогональную проекции О4А4 отрезка ОА на плоскости П4, проведенный через отрезок ОА и перпендикулярной к П1.Отложив отрезок О4А4 на прямой О1А1 и от точки О1, находим горизонтальную проекцию А¢1 точки А после поворота. Соединив точку А¢1 с точками 11 и 21, получаем проекции l¢1 и m¢1 прямых l и m после поворота. Угол j° между ними равен искомому углу.
Задача № 5.10.Определить угол между скрещивающимися прямыми h и f
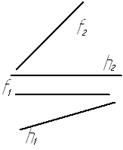
Рис. 34
Угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, параллельными заданным скрещивающимся прямым.
Через точку А на прямой h проводим прямую l, параллельную прямой f. Теперь решение задачи сводится к определению угла между пересекающимися прямыми h и l.
Угол j° между пересекающимися прямыми h и l находим поворотом плоскости, образованной прямыми h и l вокруг фронтали l этой плоскости до положения фронтальной плоскости. Отмечаем на горизонтали h точку В (В1,В2) и поворачиваем точку В вокруг фронтали l до положения В¢2 и угол между прямыми l2 и h¢2 =j°- есть искомый угол между прямыми h и f.
Задача № 5.11. Определить угол между прямой l и плоскостью a (n Ç f)
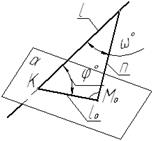
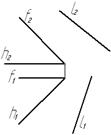
Рис. 35 Рис. 36
Углом между прямой и плоскостью считается угол между этой прямой и её ортогональной проекцией на данную плоскость. Исходя из этого, решение задачи может быть следующим. Из произвольной точки М прямой l опускаем перпендикуляр n на плоскости a. Находим точку пересечения этого перпендикуляра с плоскостью (точка Мa) и точку К пересечения прямой l с плоскостью a. Через точки К и Мa проводим прямую la - проекцию прямой l на плоскости a. Угол j° между прямыми l и la - искомый угол.
Решение задачи упрощается, если определить угол ω° ( угол между прямой l и перпендикуляром n). Зная угол ω°, определим искомый угол j°=90° - ω°. Для построения перпендикуляра n, на эпюре n1 строится перпендикулярно к h1, а n2 строится перпендикулярно к f2. Угол ω° между прямой l и перпендикуляром определяется поворотом плоскости этого угла вокруг горизонтали h*. См. решение задачи № 5.9. Угол j° получается дополнением угла ω° до 90°.
Задача № 5.12. Определить угол между плоскостями a (а Ç b) и β (с Ç d).
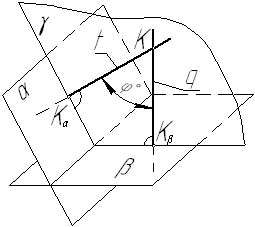
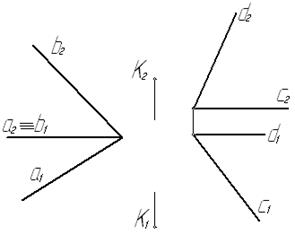
Рис.37 Рис.38
Угол между двумя плоскостями равен углу между перпендикулярами к этим плоскостям.
Из произвольной точки пространства К(К1, К2) проведены перпендикуляры t (t1 ^ a1, t2 ^ b2) к плоскости a(а Ç b) и q(q1 ^ c1, q2 ^ d2) к плоскости β(с Ç d). Плоскость перпендикуляров t и q повернута вокруг фронтали f(f1, f2) до положения фронтальной плоскости. Фронтальные проекции t¢2 и q¢2 повернутых перпендикуляров t и q образуют угол j°, равный искомому углу между двумя плоскостями a и β.
Задача № 5.13. Определить углы наклона отрезка АВ к плоскостям проекций П1 и П2.
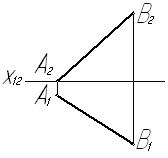
Рис. 39
Для решения задачи взята новая плоскость П4, отвечающая двум условиям: П4 ^ П1 и П4÷÷АВ. В системе П4 / П1 прямая АВ стала параллельна плоскости П4, а поэтому Х14÷÷А1В1. На плоскость П4 без искажения проецируется и отрезок АВ и угол a°, угол между прямой АВ и плоскостью проекций П1. А чтобы определить угол между прямой АВ и плоскостью проекций П2, введем ещё одну дополнительную плоскость проекций П5, отвечающую тоже двум условиям: П5^П2 и П5÷÷АВ. В системе П5 / П2 прямая АВ становится параллельна плоскости П5, и поэтому Х25÷÷А2В2. На плоскость П5 без искажения проецируется и отрезок АВ, и угол β°, угол между прямой АВ и плоскостью проекций П2.
Задача № 5.14. Определить углы наклона плоскости a(а÷÷ b) к плоскостям проекций П1 и П2.
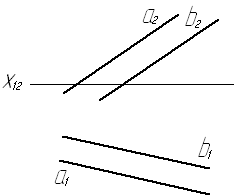
Рис. 40
Плоскость a общего положения задана двумя параллельными прямыми а и b. Для решения поставленной задачи нужно новую плоскость проекций расположить перпендикулярно a и одной из плоскостей проекций. Вот почему в заданной плоскости проводим горизонталь и фронталь. Эти линии уровня нужны для ориентировки новых плоскостей проекций П4 и П5. Расположив П4 ^ h (горизонтали плоскости), обеспечиваем выполнение двух условий: новая плоскость П4 будет перпендикулярна и П1, и плоскости a, новую ось Х14 проводим под прямым углом к h1 (горизонтальной проекции горизонтали). Новая проекция плоскости a представляет собой прямую линию a4. На плоскость П4, которая перпендикулярна плоскости a и плоскости П1, без искажения проецируется угол a, Ù П1, образованный плоскостью a с плоскостью П1.
Для определения угла, образованного плоскостью a с плоскостью проекций П2, вводим ещё одну дополнительную плоскость П5 так, чтобы П5 ^ П2 и П5 ^ a нужно расположить П5 ^ f (фронтали плоскости). На эпюре ось Х25 проводим под прямым углом к f2 (фронтальной проекции фронтали). Проекция плоскости a представляет собой прямую линию a5. На плоскости П5, которая перпендикулярна плоскости a и плоскости П2, без искажения проецируется угол a,Ù П2, образованный плоскостью a с плоскостью П2.
