Криволинейные интегралы по длине дуги
990. Вычислить криволинейный интеграл  , где L – отрезок прямой y = 0,5x – 2, заключенный между точками A(0; –2) и B(4; 0).
, где L – отрезок прямой y = 0,5x – 2, заключенный между точками A(0; –2) и B(4; 0).
991. Вычислить криволинейный интеграл 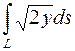 , где L – первая арка циклоиды
, где L – первая арка циклоиды 
992. Найти массу участка линии y = ln x между точками с абсциссами x1 и x2, если плотность линии в каждой точке равна квадрату абсциссы точки.
993. Найти массу четверти линии x = etcos t, y = etsin t, z = et от точки, соответствующей t = 0, до произвольной точки, если плотность дуги обратно пропорциональна квадрату полярного радиуса и в точке (1; 0; 1) равна единице.
994. Вычислить криволинейный интеграл 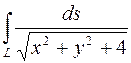 , где L – отрезок прямой, соединяющей точки O(0; 0) и A(1; 2).
, где L – отрезок прямой, соединяющей точки O(0; 0) и A(1; 2).
995. Вычислить криволинейный интеграл 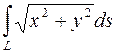 , где L – дуга развертки окружности x = a(cos t + t sin t), y = a(sin t – t cos t) [0 £ x £ 2π].
, где L – дуга развертки окружности x = a(cos t + t sin t), y = a(sin t – t cos t) [0 £ x £ 2π].
996. Найти массу участка цепной линии 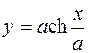 между точками с абсциссами x1= 0 и x2= a, если плотность линии в каждой ее точке обратно пропорциональна ординате точки, причем плотность в точке (0; a) равна δ.
между точками с абсциссами x1= 0 и x2= a, если плотность линии в каждой ее точке обратно пропорциональна ординате точки, причем плотность в точке (0; a) равна δ.
997. Найти массу первого витка винтовой линии x = a cos t, y = a sin t, z = bt, плотность которой в каждой точке равна квадрату полярного радиуса этой точки.
Криволинейные интегралы по координатам
Вычислить криволинейные интегралы:
998.  , где L – контур треугольника, образованного осями координат и прямой
, где L – контур треугольника, образованного осями координат и прямой  , в положительном направлении (т.е. против движения часовой стрелки).
, в положительном направлении (т.е. против движения часовой стрелки).
999. 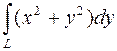 , где L – контур четырехугольника с вершинами (указанными в порядке обхода) в точках A(0; 0), B(2; 0), C(4; 4), и D(0; 4).
, где L – контур четырехугольника с вершинами (указанными в порядке обхода) в точках A(0; 0), B(2; 0), C(4; 4), и D(0; 4).
1000. 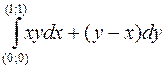 вдоль линии 1) y = x, 2) y = x2, 3) y2 = x, 4) y = x3.
вдоль линии 1) y = x, 2) y = x2, 3) y2 = x, 4) y = x3.
1001. 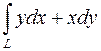 , где L – четверть окружности x = R cos t, y = R sin t, от t1 = 0 до t2 =
, где L – четверть окружности x = R cos t, y = R sin t, от t1 = 0 до t2 = 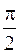 .
.
1002.  , где L – полуокружность x = a cos t, y = a sin t от t1 = 0 до t2 = π.
, где L – полуокружность x = a cos t, y = a sin t от t1 = 0 до t2 = π.
1003.  , где L – дуга параболы y = x2 от точки пересечения ее с осью абсцисс до точки пересечения ее с осью ординат.
, где L – дуга параболы y = x2 от точки пересечения ее с осью абсцисс до точки пересечения ее с осью ординат.
1004.  по отрезку от точки (0; 0) до (π; 2π).
по отрезку от точки (0; 0) до (π; 2π).
1005. 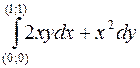 вдоль линии 1) y = x, 2) y = x2, 3) y = x3, 4) y2 = x.
вдоль линии 1) y = x, 2) y = x2, 3) y = x3, 4) y2 = x.
1006.  , где L – эллипс x = a cos t, y = b sin t, пробегаемый в положительном направлении.
, где L – эллипс x = a cos t, y = b sin t, пробегаемый в положительном направлении.
1007.  , где L – четверть астроиды x = R cos3t, y = R sin3t от точки (R; 0) до точки (0; R).
, где L – четверть астроиды x = R cos3t, y = R sin3t от точки (R; 0) до точки (0; R).
Двойные интегралы
1008. Изменить порядок интегрирования в повторном интеграле:
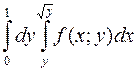 .
.
1009. Переменив порядок интегрирования, записать данное выражение в виде одного двукратного интеграла:
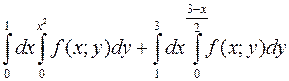 .
.
1010. Вычислить  , где D – область, ограниченная прямыми x = 2, y = x и гиперболой xy = 1.
, где D – область, ограниченная прямыми x = 2, y = x и гиперболой xy = 1.
1011. Вычислить 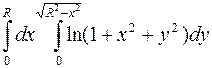 с помощью перехода к полярным координатам.
с помощью перехода к полярным координатам.
1012. Вычислить 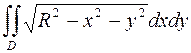 , где D – круг x2 + y2 £ Rx.
, где D – круг x2 + y2 £ Rx.
1013. Вычислить площадь, ограниченную прямыми x = y, x = 2y, x + y = a, x + 3y = a (a > 0).
1014. Изменить порядок интегрирования в повторном интеграле:
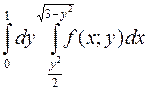 .
.
1015. Переменив порядок интегрирования, записать данное выражение в виде одного двукратного интеграла:
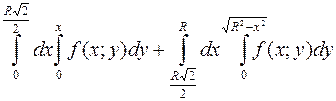 .
.
1016. Вычислить 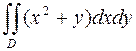 , где D – область, ограниченная параболами y = x2 и y2 = x.
, где D – область, ограниченная параболами y = x2 и y2 = x.
1017. Вычислить 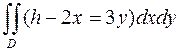 , где D – круг x2 + y2 £ R 2.
, где D – круг x2 + y2 £ R 2.
1018. Вычислить  , где D – четверть круга x2 + y2 £ 1, лежащая в первом квадранте.
, где D – четверть круга x2 + y2 £ 1, лежащая в первом квадранте.
1019. Вычислить площадь, лежащую под осью Ox и ограниченную этой осью, параболой y2 = 4ax и прямой x + y = 3a.
