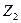Основы теории комплексных чисел
По данной теме сначала изучите главу 3 §12-17 учебника [ 3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия.
Комплексными числами называются числа вида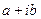 
, где a и b – действительные числа, а число i, определенное равенством 
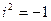, называется мнимой единицей. Для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:
1) два комплексных числа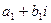 
и 
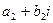называются равными, есл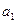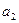и 
= 
и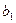 
= 
;
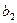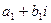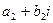2) суммой двух комплексных чисел и называется комплексное число ( 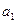+ 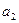)+( + 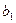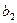)i;
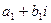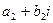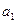
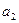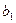
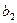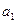
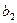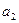
3) произведением двух комплексных чисел и называется комплексное число ( - )+ ( + 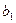)i.
Запись комплексного числа в виде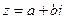 
называется алгебраической формой записи комплексного числа.
Действительное число а называется действительной частью комплексного числа 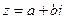, а действительное число b – мнимой частью.
Любое действительное число а содержится в множестве комплексных чисел, его можно записать так: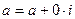 
.
При а=0 комплексное число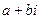 
обращается в чисто мнимое число 
.
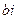Комплексное число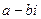 
называется комплексно сопряженным с числом 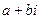и обозначается 
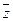, то есть 
.
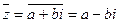Комплексные числа вида 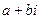и 
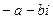называются противоположными.
Модулем комплексного числа 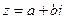называется число 
.
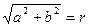Модуль комплексного числа всегда есть действительное неотрицательное число: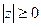 
, причем 
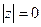тогда и только тогда, когда 
.
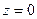Комплексное число 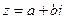можно изображать точкой плоскости с координатами 
.
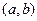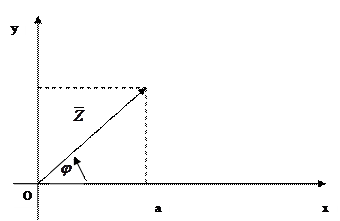При этом действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа – точками оси ординат, которую называют мнимой осью.
Каждой точке плоскости с координатами 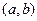соответствует один и только один вектор с началом в точке О (0, 0) и концом в точке М .
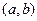Поэтому комплексное число 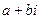можно изобразить в виде вектора 
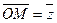с началом в точке 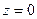и концом в точке .
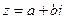Из геометрической интерпретации комплексного числа вытекают следующие свойства.
I. Длина вектор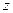а 
равна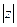 
.
II. Точки 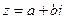и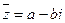 
симметричны относительно действительной оси.
III. Точки 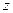и - 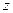симметричны относительно точки 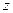=0.
|
+ 
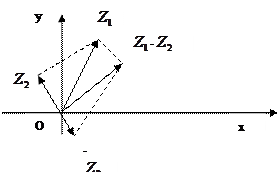
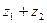геометрически изображается как вектор, построенный по правилу сложения векторов, соответствующих точкам 
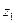и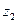 
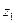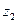V. Расстояние между точками и равно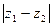 
Угол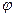 
между действительной осью Ох и вектором 
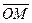, отсчитываемый от положительного направления действительной оси, называется аргументом комплексного числа 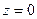. Если отсчет ведется против движения часовой стрелки, то величина угла считается положительной, а если по движению часовой стрелки – отрицательной.
Аргумент 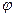комплексного числа 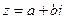записывается так:
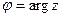или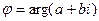 
Для числа 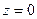аргумент не определен.
Аргумент 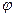комплексного числа определяется неоднозначно; любое комплексное число 
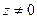имеет бесконечное множество аргументов, отличающихся друг от друга на число, кратное 
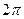. Наименьшее по абсолютной величине значение аргумента из промежутка 
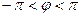называется главным значением аргумента.
Из определения тригонометрических функций следует, что если 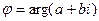, то имеют место равенства:
; 
(*)
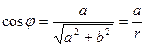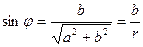Справедливо и обратное утверждение, то есть, если выполняются оба равенства, то 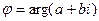. Таким образом, все значения аргумента 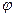можно находить, решая совместно уравнения (*).
Значения аргумента комплексного числа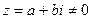 
можно находить и так:
1) определить, в какой четверти находится точка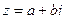 
(использовать геометрическую интерпретацию числа );
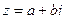2) найти в этой четверти угол 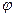, решив одно из уравнений (*) или уравнение 
;
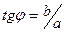3) найти все значения аргумента числа z по формуле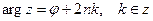 
.