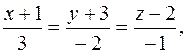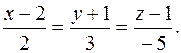Скалярное произведение векторов
57.Определить угол между векторами 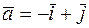 и
и 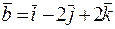 .
.
58. На плоскости дан треугольник с вершинами О(0; 0), А(2a; 0) и В(a; –a). Найти угол, образованный стороной ОВ и медианой ОМ этого треугольника.
59. Из вершины квадрата проведены прямые, делящие противоположные стороны пополам. Найти угол между ними.
60. Даны векторы 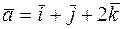 и
и 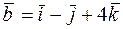 . Определить
. Определить 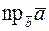 и
и 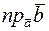 .
.
61. Вычислить: 1) 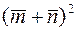 , если
, если 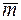 и
и 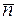 — единичные векторы с углом между ними 30°; 2)
— единичные векторы с углом между ними 30°; 2) 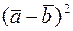 , если
, если 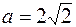 , b = 4 и угол
, b = 4 и угол 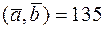 °.
°.
62. Определить длины диагоналей параллелограмма, построенного на векторах 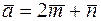 и
и 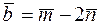 , где
, где 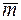 и
и 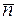 – единичные векторы, угол между которыми 60°.
– единичные векторы, угол между которыми 60°.
63. В треугольнике с вершинами А(–2; 0). В(6; 6) и С(1; –4) определить длину биссектрисы АЕ.
64. Вершины треугольника находятся в точках А(–8; –1; –4), В(–7; 3; 4) и С(8; –3; 4). Найти координаты центра тяжести треугольника, величину угла А и направляющие косинусы биссектрисы угла А.
65. Определить углы треугольника АВС с вершинами А(2; –1; 3), В(1; 1; 1) и С(0; 0; 5).
66. Даны векторы 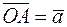 и
и 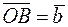 , причем a = 2, b = 4, а угол
, причем a = 2, b = 4, а угол 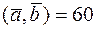 °. Определить угол между медианой
°. Определить угол между медианой 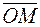 треугольника АОВ и стороной
треугольника АОВ и стороной 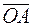 .
.
67. Из вершины прямоугольника со сторонами 6см и 4см проведены прямые, делящие противоположные стороны пополам. Найти угол jмежду ними.
68. Даны три последовательные вершины параллелограмма: А(–3; –2; 0), В(3; –3; 1) и С(5; 0; 2). Найти его четвертую вершину D и угол между векторами 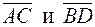 .
.
69. Даны точки А(3; 3; –2), В(0; –3; 4), С(0; –3; 0) и D(0; 2; –4). Построить векторы 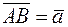 и
и 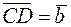 и найти
и найти 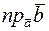 .
.
70. В равнобедренной трапеции ОАСВ (рис. 2) М и N – середины сторон ВС = 2 и АС = 2. Острый угол трапеции 60°. Определить угол между векторами 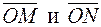 .
.
71. Проекции перемещения движущейся точки на оси координат sx = 2, sy = 1, sz = –2м. Проекции действующей силы 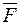 на оси координат равны Fx = 5H, Fy = 4H, и Fz = 3H. Вычислить работу А силы
на оси координат равны Fx = 5H, Fy = 4H, и Fz = 3H. Вычислить работу А силы 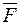 (A =
(A = 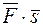 ) и угол между силой
) и угол между силой 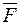 и перемещением
и перемещением 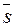 .
.
§6. Векторное и смешанное произведения векторов
72. Векторы 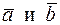 образуют угол
образуют угол 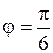 . Зная, что
. Зная, что 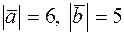 , вычислить
, вычислить 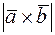 .
.
73. Даны 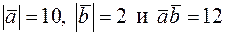 . Вычислить
. Вычислить 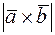 .
.
74. Даны векторы 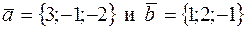 . Найти координаты векторных произведений: 1)
. Найти координаты векторных произведений: 1) 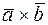 , 2)
, 2) 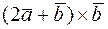 , 3)
, 3) 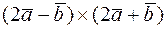 .
.
75. Вычислить площадь треугольника с вершинами A(7; 3; 4), B(1; 0; 6) и C(4; 5; -2).
76. Сила 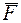 = {3; 2; -4} приложена к точке A(2; -1; 1). Определить момент этой силы относительно начала координат.[1]
= {3; 2; -4} приложена к точке A(2; -1; 1). Определить момент этой силы относительно начала координат.[1]
77. Векторы 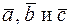 , образующие правую тройку, взаимно перпендикулярны. Зная, что
, образующие правую тройку, взаимно перпендикулярны. Зная, что 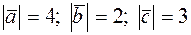 , вычислить
, вычислить 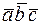 .
.
78. Даны три вектора: 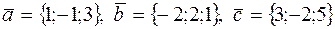 . Вычислить
. Вычислить 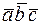 .
.
79. Сила 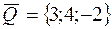 приложена к точке C(2; -1; -2). Определить величину и направляющие косинусы момента этой силы относительно начала координат.
приложена к точке C(2; -1; -2). Определить величину и направляющие косинусы момента этой силы относительно начала координат.
80. Вычислить объем тетраэдра, вершины которого находятся в точках A(2; -1; 1), B(5; 5; 4), C(3; 2; -1) и D(4; 1; 3).
81. Даны 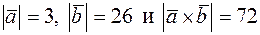 . Вычислить
. Вычислить 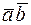 .
.
82. Векторы 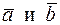 образуют угол
образуют угол 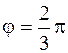 . Зная, что
. Зная, что 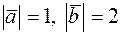 вычислить: 1)
вычислить: 1) 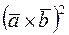 , 2)
, 2) 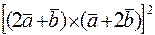 , 3)
, 3) 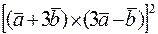 .
.
83. Даны точки A(2; -1; 2), B(1; 2; -1) и C(3; 2; 1). Найти координаты векторных произведений: 1) 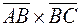 ; 2)
; 2) 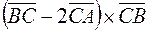 .
.
84. Дан треугольник с вершинами A(1; -2; 8), B(0; 0; 4) и C(6; 2; 0). Вычислить его площадь и высоту BD.
85. Сила 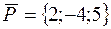 приложена к точке M0(4; -2; 3). Определить момент этой силы относительно точки A(3; 2; -1).
приложена к точке M0(4; -2; 3). Определить момент этой силы относительно точки A(3; 2; -1).
86. Сила 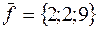 приложена к точке A(4; 2; -3). Определить величину и направляющие косинусы момента этой силы относительно точки C(2; 4; 0).
приложена к точке A(4; 2; -3). Определить величину и направляющие косинусы момента этой силы относительно точки C(2; 4; 0).
87. Вектор 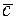 перпендикулярен к векторам
перпендикулярен к векторам 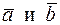 , угол между
, угол между 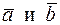 равен 30°. Зная что
равен 30°. Зная что 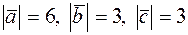 , вычислить
, вычислить 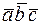 .
.
88. Установить, компланарны ли векторы 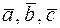 , если:
, если:
1) 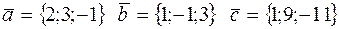 ;
;
2) 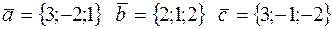 ;
;
3) 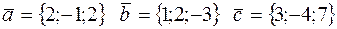 .
.
89. Даны вершины тетраэдра: A(2; 3; 1), B(4; 1; -2), C(6; 3; 7), D(-5; -4; 8). Найти длину его высоты, опущенной из вершины D.
§7. Плоскость и прямая в пространстве
90. Точка Р(2; -1; -1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.
91. Составить уравнение плоскости, проходящей через точку М1(3; 4; -5) параллельно двум векторам 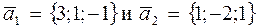 .
.
92. Составить уравнение плоскости, проходящей через три точки M1(3; -1; 2), M2(4; -1; -1), и M3(2; 0; 2).
93. Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 5x - 3y + 2z - 3 = 0.
94. Составить уравнение плоскости, которая проходит через точку M1(2; -1; 1) перпендикулярно к двум плоскостям: 2x - z + 1 = 0, y = 0.
95. Две грани куба лежат на плоскостях 2x - 2y + z - 1 = 0, 2x - 2y + z + 5 = 0. Вычислить объем этого куба.
96. Составить канонические уравнения прямой, проходящей через точку M1(2; 3; -5) параллельно прямой 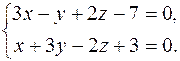
97. составить уравнения прямой, проходящей через точку M0(2; -3; -5) перпендикулярно к плоскости 6x - 3y - 5z + 2 = 0.
98. Даны две точки M1(3; -1; 2) и M2(4; -2; -1). Составить уравнение плоскости, проходящей через точку M1 перпендикулярно вектору 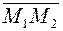 .
.
99. Составить уравнение плоскости, проходящей через точки M1(2; -1; 3) и M2(3; 1; 2) параллельно вектору 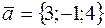 .
.
100. Составить уравнение плоскости, которая проходит через точку M1(3; -2; -7) параллельно плоскости 2x - 3z + 5 = 0.
101. Составить уравнение плоскости, которая проходит через две точки M1(1; -1; -2) и M2(3; 1; 1) перпендикулярно к плоскости x - 2y + 3z - 5 = 0.
102. Установить, что три плоскости x - 2y + z - 7 = 0, 2x + y - z + 2 = 0, x - 3y + 2z - 11 = 0 имеют одну общую точку и вычислить ее координаты.
103. Вычислить расстояние d от точки P(-1; 1; -2) до плоскости, проходящей через три точки M1(1; -1; 1), M2(-2; 1; 3) и M3(4; -5; -2).
104. Даны прямые: 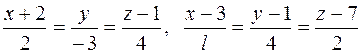 . при каком значении l они пересекаются?
. при каком значении l они пересекаются?
105. Составить уравнение плоскости, проходящей через точку M0(1; -2; 1) перпендикулярно к прямой 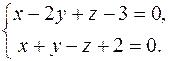
106. Составить уравнения прямой, которая проходит через точку M1(-4; -5; 3) и пересекает две прямые: