Сложное сопротивление – задание № 4
Сложное сопротивление – это такой случай нагружения деформируемого тела, когда в произвольном поперечном сечении возникают несколько внутренних усилий. Порядок оценки прочности элементов конструкции при сложном сопротивлении почти не отличается от общего порядка расчета, изложенного во введении (см. стр4).
Единственное, на что надо обратить особое внимание, заключается в следующем:
- в опасной точке могут действовать напряжения одного вида (только касательные «τ» или только нормальные «  » ) или разного –
» ) или разного –  , τ – и касательные и нормальные. Для определения максимального расчетного (эквивалентного) значения напряжения в первом случае применяют алгебраическое суммирование действующих напряжений от каждого внутреннего усилия, во втором случае – теории прочности, чаще всего III и IV теории, когда эквивалентные напряжения определяют по формулам:
, τ – и касательные и нормальные. Для определения максимального расчетного (эквивалентного) значения напряжения в первом случае применяют алгебраическое суммирование действующих напряжений от каждого внутреннего усилия, во втором случае – теории прочности, чаще всего III и IV теории, когда эквивалентные напряжения определяют по формулам:  эIII =
эIII = 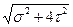 ,
,  эIV =
эIV = 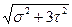 (30)
(30)
Наиболее частыми случаями сложного сопротивления, встречающимися в инженерной практике, являются косой изгиб, изгиб с растяжением (сжатием), кручение с изгибом.
Косой изгиб - возникает тогда, когда плоскость действия внешней нагрузки (силовая плоскость) не совпадает с плоскостями главных осей инерции поперечного сечения. Для удобства расчета внешнюю нагрузку раскладывают на составляющие по главным осям, сводя таким образом косой изгиб к сочетанию 2-х прямых изгибов, строятся эпюры изгибающих моментов в обоих плоскостях и по ним определяется положение опасного сечения. Расчет ведут обычно только по нормальным напряжениям. Тогда расчетное (эквивалентное) напряжение будет равно:
 э =
э =  Мх +
Мх +  Му =
Му = 
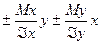 (31)
(31)
где Мх и Му – изгибающие моменты относительно главных осей сечения;
Ix, Iy – осевые моменты инерции;
х, у – координаты точки, где определяется напряжение;
Для определения опасных точек, где действуют максимальные напряжения, предварительно определяется положение нейтральной линии
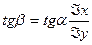
где α – угол с осью у, определяющий положение силовой плоскости;
β – угол с осью х, который образует нейтральная линия (см. рис.52)
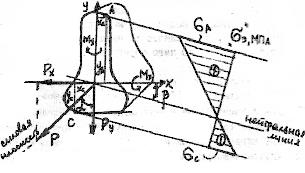
Рис 52
Проведя касательные к контуру сечения, параллельно нейтральной линии, устанавливаем две опасные точки «C» и «A», в которых напряжения будут равны 
 а=
а= 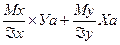 (33)
(33)
 с= -
с= - 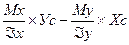
В данном случае в т. А действуют растягивающие напряжения, в т. «С» - сжимающие.
Для материала бруса, одинаково сопротивляющегося растяжению и сжатию, прочность оценивается по наиболее опасной точке, например «А».
 а=
а= 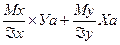
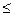 [
[  ] (34)
] (34)
Для материалов, неодинаково сопротивляющихся растяжению и сжатию, прочность оценивается в обеих опасных точках и прежде всего, по растягивающим напряжениям
 а=
а= 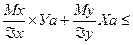 [
[  ]р (35)
]р (35)
 с= -
с= - 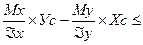 [
[  ]сис
]сис
В случае сочетания центрального растяжения (сжатия) с прямым изгибом суммарное (эквивалентное) напряжение в опасных точках будет равно
 э=
э=  N +
N +  Мх =
Мх = 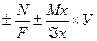 (36)
(36)
Естественно, оно будет максимальным в тех волокнах сечения, где оба напряжения – от продольной силы N и изгибающего момента имеют одинаковый знак.
В случае сочетания центрального растяжения (сжатия) с косым изгибом суммарное (эквивалентное) напряжение равно
 э=
э=  N +
N +  Мх +
Мх +  Му=
Му= 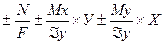 (37)
(37)
Опасные точки сечения определяются как в случае косого изгиба, т.е. устанавливается положение нейтральной линии (формула 32) и проводятся касательные к контуру сечения параллельно нейтральной линии. Прочность оценивается по формулам (34) или (35) с добавлением в них третьего слагаемого – напряжение от продольной силы N.
В случае вне центрового приложения осевой нагрузки (см.рис.53) суммарное (эквивалентное) напряжение в опасных точках определяется из выражения
 э=
э=  N +
N +  Мх +
Мх +  Му =
Му = 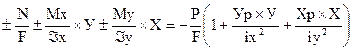 (38)
(38)
где N=p – продольная сила;
Мх=P 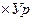 - изгибающий момент относительно оси Х;
- изгибающий момент относительно оси Х;
Му=P 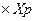 - то, же, относительно оси У;
- то, же, относительно оси У;
Хр, Ур – координаты точки приложения осевой силы (полюс силы)
ix, iу – радиусы инерции сечения, которые равны ix= 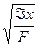 ; iу=
; iу= 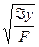
 Х, У – координаты точки, в которой определяется напряжение
Х, У – координаты точки, в которой определяется напряжение
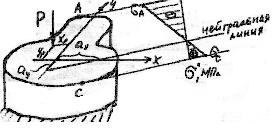
Рис. 53
Для нахождения опасных точек определим положение нейтральной линии по отрезкам
ах= - 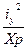 ; ау= -
; ау= - 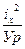 (39)
(39)
Отсюда видно, что нейтральная линия и полюс силы находятся по разные стороны от центра тяжести сечения (см.рис.53).
В нашем случае наибольшее сжимающее напряжение действует в точке «А».
 а= -
а= - 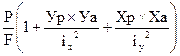 (40)
(40)
а наибольшее растягивающее напряжение в точке «С».
 с= -
с= - 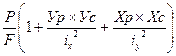 (41)
(41)
Сравнивая эти напряжения с допускаемым напряжением делаем вывод, о прочности растянутого или сжатого стержня. В случае совместного действия деформаций кручения и изгиба расчет на прочность ведут, как правило, с учетом нормальных напряжений от изгибающих моментов и касательных напряжений от крутящего момента. Для удобства выполнения расчета, все внешние силы, обычно действующие в разных плоскостях и направлениях, раскладывают на составляющие в вертикальной и горизонтальной плоскостях и строят соответствующие эпюры изгибающих моментов Мх, Му. По эпюрам Мх, Му, Мк определяют опасное сечение, в котором эти внутренние усилия имеют максимальное значение. Если по эпюрам не удается достоверно сразу установить опасное сечение, то проверяется несколько предположительно опасных сечений, в которых суммарный изгибающий момент максимален
Мn = 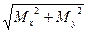 (42)
(42)
В опасном сечении наибольшие напряжения от кручения и изгиба действуют в крайних (к поверхности) волокнах и расчетное (эквивалентное) напряжение определяют с использованием III и IV теории прочности (см. формулы 30). Так, по III теории прочности с учетом выражений (16), (22) будем иметь
 эIII =
эIII = 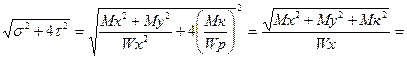
= 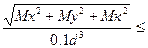 [
[  ] (43)
] (43)
Отсюда получаем формулу для определения диаметра вала при выполнении проектного расчета
d = 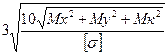 (44)
(44)
Примеры решения задач
Задача № 37
Проверить прочность двутавровой балки №60, α=600,
[σ]=150Мпа (рис. 54)
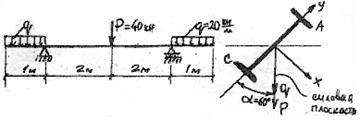
Рис. 54
Решение. 1.Анализируя схему нагружения балки видим, что плоскость действия внешних сил не совпадает с главными осями инерции сечения балки. Следовательно, балка испытывает косой изгиб. Определим составляющие внешних сил по главным осям инерции
qу = qcosα = 20х0,5=10 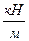 ; qх= qsinα = 20х0,866
; qх= qsinα = 20х0,866 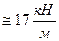
Ру= 40х0,5=20кН; Рх= 40х0,866 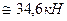
2. Нагружаем балку силами, действующими в плоскости oyz, определяем опорные реакции и строим эпюру изгибающих моментов Мх
(см. рис.55 а, б)
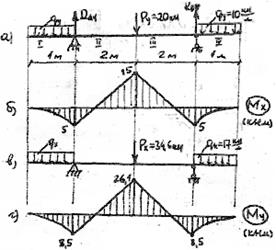
Рис. 55
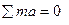 -
- 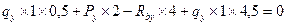
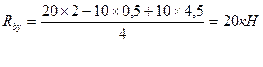
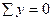
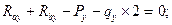 Ra=20кН
Ra=20кН
1 участок 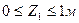
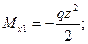
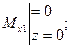
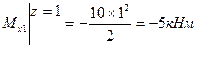
2 участок 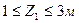
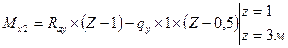
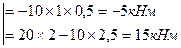
3 участок 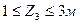
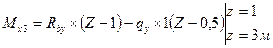
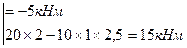
4 участок 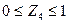
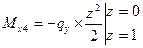
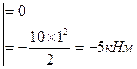
3. Нагружаем балку силами, действующими в плоскости oxz, определяем реакции опор и строим эпюру изгибающих моментов Му (см. рис. 55в, г)
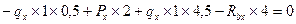
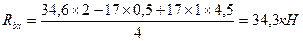
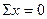
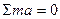
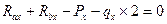
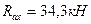
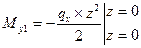
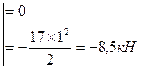
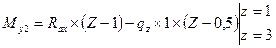
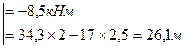
4. Из эпюр Мх и Му видим, что опасное сечение балки находится под силой Р. Поскольку сечение балки симметрично, в опасных точках одновременно Х и У достигают максимального значения, формулу (34) для эквивалентного напряжения приводим к виду
 э=
э=  мх+
мх+  му=
му= 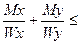 [
[  ] (45)
] (45)
Здесь Wx и Wy – осевые моменты сопротивлению изгибу заданного сечения балки. Из сортамента ГОСТ – 8239 – 89 для №60 двутавра
Wx=2560см3; Wy=182см3.
 э=
э= 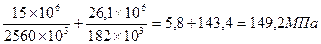 ъ
ъ
Таким образом  э<[
э<[  ] = 150МПа, т.е. прочность балки обеспечена.
] = 150МПа, т.е. прочность балки обеспечена.
Задача №38
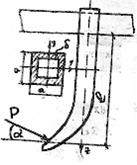 Определить, с каким запасом прочности будет работать стойка АВ лапы культиватора (рис.56), если она будет изготовлена из стали 45, имеющей
Определить, с каким запасом прочности будет работать стойка АВ лапы культиватора (рис.56), если она будет изготовлена из стали 45, имеющей  т=360МПа. Сечение стойки –квадратная тонкостенная труба размерами а=45мм, б=3мм. Полное давление почвы на лапу Р=1,2кн и направлено под углом α=180 к горизонтали, l=0,45м.
т=360МПа. Сечение стойки –квадратная тонкостенная труба размерами а=45мм, б=3мм. Полное давление почвы на лапу Р=1,2кн и направлено под углом α=180 к горизонтали, l=0,45м.
Рис. 56
Решение
1.Если разложить силу Р на две составляющие – вдоль (Рz) и перпендикулярно (Ру) оси стойки, то увидим, что они будут вызывать деформации соответственно растяжения и прямого изгиба. Опасное сечение будет совпадать с закреплением стойки, там будет действовать продольная сила N=Pz=Psinα и наибольший изгибающий момент Мх=РуL=PcosαL
2. Расчетное (эквивалентное) напряжение в случае сочетания растяжения с прямым изгибом равно (см. формулу 36)
 э=
э= 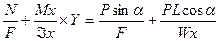
3.Для тонкостенного квадратного сечения согласно [2] площадь сечения F=4б 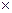 а, а осевой момент сопротивления Wx=
а, а осевой момент сопротивления Wx= 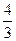 а2
а2 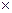 б.
б.
Тогда  э=
э= 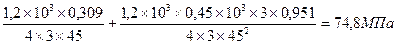
4.Из условия прочности  э
э 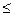 [
[  ]=
]= 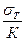 определим запас прочности стойки
определим запас прочности стойки
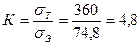 что вполне достаточно.
что вполне достаточно.
Задача №39
На валу привода двух вентиляторов зерносушилки расположены 3 шкива (звездочки) диаметром Д1=200мм, Д2=400мм, Д3=300мм, шкив 2 ведущий, передает мощность N2=4,8кВт, 1 и 3 шкивы – ведомые, передающие мощность N1=1,8кВт, N3=3,0кВт при частоте вращения вала n=955 об/мин. Определить диаметр вала по III теории прочности, если α2=600
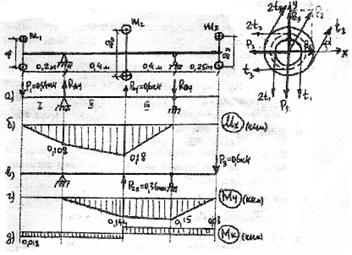
Рис. 57
Решение:
1.Рассматривая схему нагружения вала видим, что он испытывает деформацию кручения в сочетании с изгибом в 2-х плоскостях.
2.Определяем внешние (скручивающие) моменты, передаваемые каждым шкивом
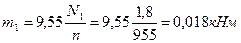
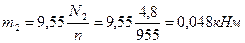
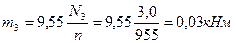
3.Определяем натяжение ветвей ременной (цепной)передачи t1, t2, t3 и полные давления на вал p1, p2, p3.
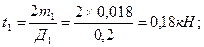
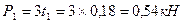
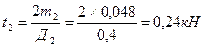 ;
; 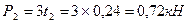
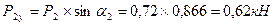 ;
; 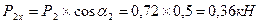
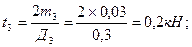
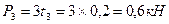
4.Нагружаем вал внешней нагрузкой, действующей в вертикальной плоскости, определяем опорные реакции и строим эпюру изгибающих моментов Мх (рис. 57 а, б).
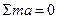
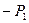
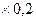 -Р2у
-Р2у 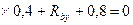 ;
; 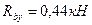
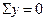 -
- 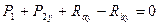 ;
; 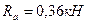
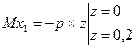
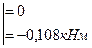
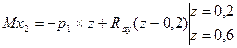
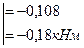
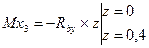
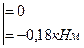
5.Нагружаем вал внешней нагрузкой, действующей в горизонтальной плоскости, определяем реакции опор и строим эпюру изгибающих моментов «Му» (рис. 57 в, г).
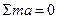 -
- 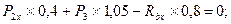
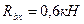
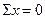 -
- 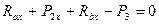 ;
; 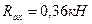
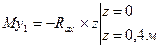
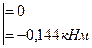
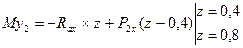
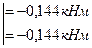
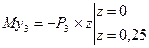
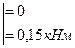
(неточность счета)
6.Строим эпюру крутящих моментов (рис. 57 д).
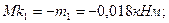
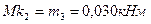
7.По эпюрам Мх, Му, Мк устанавливаем, что опасное сечение находится под ведущим шкивом 2, где Мх=0,18кНм; Му=0,144кНм; Мк=0,03кНм.
8.Определяем диаметр вала по III теории прочности (см. формулу 44).
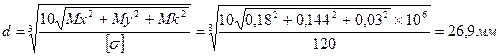
Округляем диаметр до ГОСТовского размера α=30мм.
Варианты домашних заданий.
В домашнем задании №4 предусматривается решение 4-х задач на сложное сопротивление. Номера задач в соответствии с вариантом выданным преподавателем, берутся из таблицы 5.
ТАБЛИЦА 5
Варианты домашних заданий № 4
| Вариант | Номера задач | |||
| первой | второй | третьей | Четвертой | |
| 40-1 | 43-4 | 47-1 | 45-1 | |
| 40-2 | 42-1 | 47-2 | 45-2 | |
| 40-3 | 42-2 | 47-3 | 45-3 | |
| 40-4 | 42-3 | 47-4 | 45-4 | |
| 40-5 | 42-4 | 48-1 | 45-5 | |
| 41-1 | 42-2 | 48-2 | 46-1 | |
| 41-2 | 43-1 | 48-3 | 46-2 | |
| 41-3 | 43-2 | 48-4 | 46-3 | |
| 41-4 | 43-3 | 49-1 | 46-4 | |
| 44-1 | 43-4 | 49-2 | 40-1 | |
| 44-2 | 45-3 | 49-3 | 40-2 | |
| 44-3 | 45-4 | 49-4 | 40-3 | |
| 44-4 | 45-5 | 47-1 | 40-4 | |
| 45-1 | 42-1 | 47-2 | 40-5 | |
| 45-2 | 42-2 | 47-3 | 49-1 | |
| 45-3 | 42-3 | 47-4 | 49-2 | |
| 45-4 | 42-4 | 48-1 | 49-3 | |
| 45-5 | 42-5 | 48-2 | 49-4 | |
| 46-1 | 43-1 | 48-3 | 49-5 | |
| 46-2 | 43-2 | 48-4 | 40-1 | |
| 46-3 | 43-3 | 49-1 | 40-2 | |
| 46-4 | 43-4 | 49-2 | 40-3 | |
| 42-1 | 41-2 | 49-3 | 40-4 | |
| 42-2 | 41-3 | 49-4 | 40-5 | |
| 42-3 | 40-1 | 49-5 | 47-1 | |
| 42-4 | 40-2 | 48-1 | 47-2 | |
| 42-5 | 40-3 | 48-2 | 47-3 | |
| 43-1 | 40-4 | 48-3 | 47-4 | |
| 43-2 | 40-5 | 48-4 | 46-1 | |
| 43-3 | 41-1 | 47-4 | 49-4 |
Задача № 40
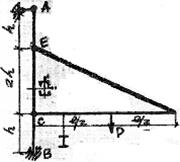 Настенный поворотный кран (рис. 58)
Настенный поворотный кран (рис. 58)
состоит из стойки АВ, несущей балки СД и тяги ДЕ, соединенных шарнирно. Определить размеры поперечных сечений стойки АВ (из 2-х швеллеров) и балки СД (двутавр), приняв допускаемое напряжение [ 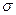 ].
].
| Позиция | Размеры, м | Р, кН | 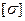 , МПа , МПа | |
| H | l | |||
| 40-1 | 0,50 | 2,4 | ||
| 40-2 | 0,75 | 3,0 | ||
| 40-3 | 1,00 | 3,4 | ||
| 40-4 | 0,80 | 2,8 | ||
| 40-5 | 1,2 | 3,6 |
Рис.58
Задача № 41
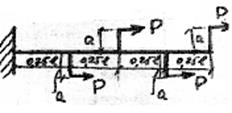
Несущая балка АВ сцепки нагружена, как указано на Рис. 59. Она сварена из 2-х швеллеров. Определить нормальные напряжения, возникающие в наиболее опасном сечении и запас прочности К, если материал балки имеет предел текучести 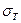 .
.
Рис. 59
| Позиции | Р, кН | а, м | l, м | № швеллера | 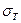 , МПа , МПа |
| 41-1 | 1,5 | 2,0 | |||
| 41-2 | 1,2 | 2,4 | |||
| 41-3 | 7,5 | 2,0 | 3,0 | ||
| 41-4 | 1,0 | 2,8 |
Задача № 42
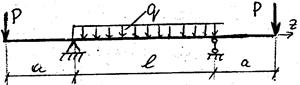
Рис. 60
Балка жнём комбайна нагружена, как указано на рис. 60. Определить наибольшее напряжение в опасном сечении балки и установить ее запас прочности, если она изготовлена из стали с 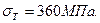
| Позиция | Нагрузка | № двутавра | α, 0 | l, | а, м | |
| Р, кН | q, 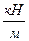 | |||||
| 42-1 | 4,0 | 0,8 | ||||
| 42-2 | 3,6 | 1,0 | ||||
| 42-3 | 3,2 | 1,2 | ||||
| 42-4 | 3,0 | 0,7 | ||||
| 42-5 | 4,8 | 0,6 |
Задача № 43
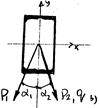
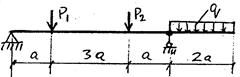
Рис. 61
Заданная балка, сваренная из 2-х швеллеров, нагружена как указано на рис. 61. Определить наибольшее напряжение, возникающее в наиболее опасном сечении. Какую сталь вы предложите для изготовления указанной балки (марка, 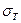 =360 МПа)
=360 МПа)
| Позиция | Нагрузка | а, м | α1, 0 | α2, 0 | № швеллера | ||
| Р1, кН | Р2, кН | q, 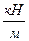 | |||||
| 43-1 | 1,0 | ||||||
| 43-2 | 1,5 | ||||||
| 43-3 | 0,8 | ||||||
| 43-4 | 1,8 |
Задача № 44
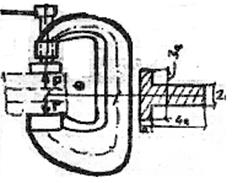 Определить допустимую нагрузку «F» для струбцины (рис. 62) с указанным сечением, изготовленной из стали с пределом текучести
Определить допустимую нагрузку «F» для струбцины (рис. 62) с указанным сечением, изготовленной из стали с пределом текучести 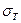 и запасом прочности «К».
и запасом прочности «К».
| Позиция | Размеры, мм | 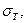 МПа МПа | К | |
| a | е | |||
| 44-1 | 1,5 | |||
| 44-2 | 2,0 | |||
| 44-3 | 1,8 | |||
| 44-4 | 2,2 |
Рис. 62
Задача № 45
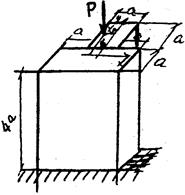 Подставка (рис. 63) заданного сечения нагружена внеценнтренно силой Р, имеющей координаты Хр, Ур. Определить положение опасных точек и величину действующих в них напряжений.
Подставка (рис. 63) заданного сечения нагружена внеценнтренно силой Р, имеющей координаты Хр, Ур. Определить положение опасных точек и величину действующих в них напряжений.
| Позиция | Координаты, мм | Р, кН | а, мм | |
| Хр | Ур | |||
| 45-1 | -25 | |||
| 45-2 | ||||
| 45-3 | -40 | |||
| 45-4 | -60 | -80 | ||
| 45-5 | -50 |
Рис.63
Задача № 46
| Позиция | Р, кН | Размеры, мм | К | е, мм | |
| а | в | ||||
| 46-1 | 52,0 | 1,5 | |||
| 46-2 | 62,5 | 1,8 | |||
| 46-3 | 83,5 | 2,0 | |||
| 46-4 | 104,0 | 1,7 |
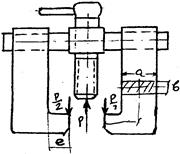
Определить напряжения в захватах съемника (рис. 64), имеющих прямоугольное сечение с размерами «а» и «в» и указать марку стали с соответствующим пределом текучести (для изготовления захватов), чтобы был обеспечен в необходимый запас по прочности «К».
Рис. 64
Задача № 47
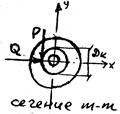
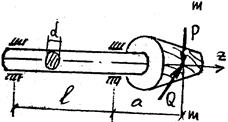
Рис. 65
Проверить прочность валика ведущей шестерни автомобиля, передающей момент Мк. На зубья шестерни действуют окружное усилие Р и радиальное давление Q=6,4Р. Валик изготовлен из стали 40 ХН и должен работать с запасом прочности «К». Расчетный средний диаметр шестерни равен Дк.
Расчет вести по III теории прочности.
| Позиция | М, кНм | Размеры, мм | К | |||
| Дк | d | а | l | |||
| 47-1 | 0,8 | 2,0 | ||||
| 47-2 | 1,0 | 2,5 | ||||
| 47-3 | 1,2 | 1,8 | ||||
| 47-4 | 0,6 | 1,5 |
 Задача № 48
Задача № 48
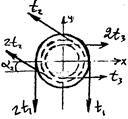
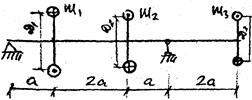
Рис. 66
Подобрать диаметр вала ременной передачи по III теории прочности, передающего с помощью трех шкивов внешние скручивающие моменты м1, м2, м3. Допускаемое напряжение для материала равно 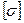 .
.
| Позиция | Внешние моменты, кНм | Диаметры шкивов, мм | а, м | 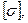 МПа МПа | α2 | ||||
| м1 | м2 | м3 | Д1 | Д2 | Д3 | ||||
| 48-1 | 1,2 | 0,8 | 0,4 | 0,25 | 300 | ||||
| 48-2 | 2,0 | 1,6 | 0,4 | 0,4 | 450 | ||||
| 48-3 | 2,5 | 1,5 | 1,0 | 0,3 | 600 | ||||
| 48-4 | 1,8 | 1,2 | 0,6 | 0,35 | 900 |
Задача № 49
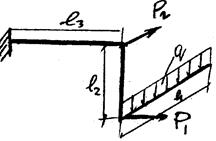
Для заданного пространственно ломанного стержня опорного устройства построить эпюры внутренних усилий и определить величину расчетных
(эквивалентных) напряжений по IV теории прочности.
Рис. 67
