Кинематика рядовых механизмов
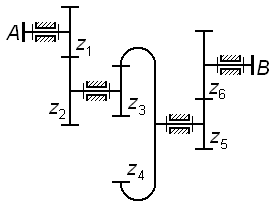
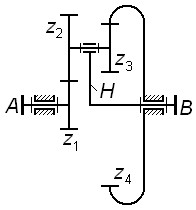
Зубчатый механизм, у которого все звенья вращаются вокруг неподвижных осей, называют рядовым. Такой механизм может быть одноступенчатым (рис. 3.1 и 3.2) и многоступенчатым(рис. 3.3
и 3.4).
В многоступенчатом рядовом механизме число ступеней совпадает с числом зацеплений, его общее передаточное отношение определяют как произведение передаточных отношений всех последовательно соединенных ступеней.
 |  | |
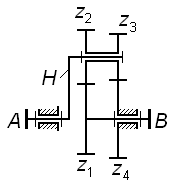
| Рис. 3.3 | Рис. 3.4 |
Так, для трехступенчатого механизма по рис. 3.3 общее передаточное отношение 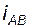 определится по формуле
определится по формуле
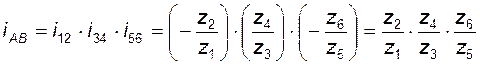 .
.
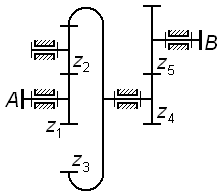
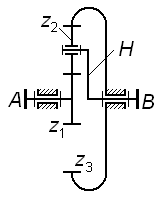
На рис. 3.4 также представлен трехступенчатый механизм, у которого колеса 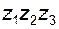 образуют соосную кинематическую цепь, причем колесо
образуют соосную кинематическую цепь, причем колесо 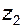 участвует одновременно в двух зацеплениях – в одном как ведомое, в другом как ведущее (такие колеса называют связанными); для этого механизма
участвует одновременно в двух зацеплениях – в одном как ведомое, в другом как ведущее (такие колеса называют связанными); для этого механизма
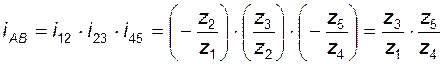 .
.
Отметим, что при 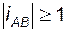 (выходной вал B вращается медленнее входного вала A) механизм называют редуктором, а при
(выходной вал B вращается медленнее входного вала A) механизм называют редуктором, а при
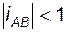 – мультипликатором.
– мультипликатором.
3.2. Кинематика планетарных и дифференциальных
механизмов
Планетарные и дифференциальные механизмы включают в себя колеса, оси которых являются подвижными. Рычаг, на котором расположены эти оси, называют водилом, а колеса с подвижными осями – сателлитами. Неподвижная ось вращения водила является центральной осью механизма. Колеса, которые вращаются или могут вращаться относительно центральной оси и при этом зацепляются с сателлитами, называют центральнымиилисолнечными.
В планетарную ступень входят: водило; сателлиты, размещенные на этом водиле; колеса, которые зацепляются с этими сателлитами.
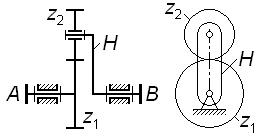 |
| Рис. 3.5 |
На рис. 3.5 представлен простейший планетарный механизм, состоящий из водила H, центрального колеса 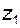 и сателлита
и сателлита 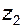 .
.
Колесо 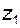 и водило H вращаются относительно центральной оси механизма.
и водило H вращаются относительно центральной оси механизма.
Сателлит 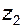 совершает сложное движение, состоящее из двух вращательных: вокруг своей геометрической оси и одновременно, вместе с водилом, вокруг центральной оси механизма.
совершает сложное движение, состоящее из двух вращательных: вокруг своей геометрической оси и одновременно, вместе с водилом, вокруг центральной оси механизма.
У этого механизма две степени свободы
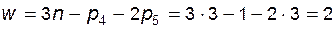 ,
,
поэтому его называют дифференциальным механизмом, или дифференциалом. Кинематику такого механизма можно описать формулой
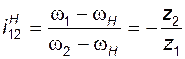 ; (3.4)
; (3.4)
здесь 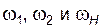 – абсолютные угловые скорости соответствующих звеньев (величины алгебраические – положительные или отрицательные),
– абсолютные угловые скорости соответствующих звеньев (величины алгебраические – положительные или отрицательные), 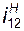 – передаточное отношение обращенного механизма (т.е. такого воображаемого рядового механизма, который получают из заданного планетарного мысленной остановкой водила).
– передаточное отношение обращенного механизма (т.е. такого воображаемого рядового механизма, который получают из заданного планетарного мысленной остановкой водила).
Из (3.4) видно, что для кинематической определимости этого механизма из трех угловых скоростей две должны быть заданы, т.е. механизм действительно является дифференциалом.
Общий вид формулы (3.4), пригодный для описания кинематики практически любого планетарного механизма, имеет вид
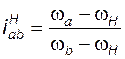 ; (3.5)
; (3.5)
ее называют формулой Р. Виллиса. Здесь a и b – любые два колеса одной и той же планетарной ступени, 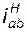 – передаточное отношение от a к b в обращенном (рядовом) механизме, это отношение всегда выражается через числа зубьев колес.
– передаточное отношение от a к b в обращенном (рядовом) механизме, это отношение всегда выражается через числа зубьев колес.
Величины угловых скоростей 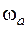 и
и 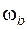 могут быть любыми; в частности, при
могут быть любыми; в частности, при 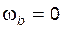 (т.е. колесо b неподвижно) отношение
(т.е. колесо b неподвижно) отношение 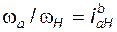 , и тогда формула Р. Виллиса приобретает вид
, и тогда формула Р. Виллиса приобретает вид
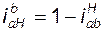 . (3. 6)
. (3. 6)
Формула (3.5) более универсальна и пригодна для любого планетарного механизма, тогда как (3.6) можно применять только для таких планетарных ступеней, у которых имеются неподвижные колеса
(рис. 3.6 – 3.8).
 |  |  |
| Рис. 3.6 | Рис. 3.7 | Рис. 3.8 |
На рис. 3.6 показана схема редуктора Джемса с двухвенцовым сателлитом. Для него
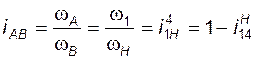 , (3. 7)
, (3. 7)
передаточное отношение обращенной ступени
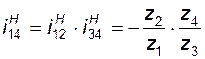 ; (3. 8)
; (3. 8)
сопоставляя (3.7) и (3.8), найдем передаточное отношение редуктора
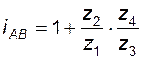 . (3. 9)
. (3. 9)
Таким же способом найдем передаточное отношение редуктора Джемса с одновенцовым сателлитом (рис. 3.7):
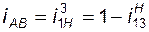 , (3.10)
, (3.10)
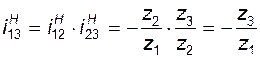 ; (3.11)
; (3.11)
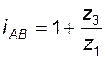 . (3. 12)
. (3. 12)
Для редуктора Давида (рис. 3.8), также имеющего неподвижное колесо в составе ступени, входным звеном является водило H, что отличает эту схему от двух других при выводе формулы для 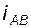 :
:
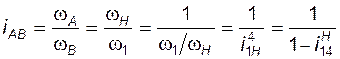 ; (3.13)
; (3.13)
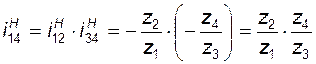 ; (3. 14)
; (3. 14)
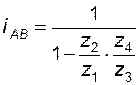 . (3. 15)
. (3. 15)
В этих примерах показано применение формулы Виллиса в виде (3.6), хотя было бы вполне корректным и допустимым использование ее в виде (3.5).
Все схемы по рис. 3.6 – 3.8 имеют в своем составе три центральных звена – два центральных колеса и водило; каждое из этих звеньев нагружено вращающим моментом либо от источника движения, либо от потребителя мощности (ведомого звена), либо моментом от стойки. Такие звенья называют основными и в соответствии с их видом и количеством (в данном случае – два колеса и водило) подобным схемам присвоено обозначение типа 2KH.
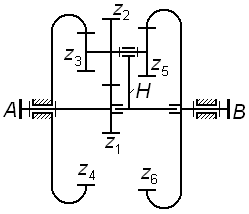 |
| Рис. 3.9 |
На рис. 3.9 приведена схема планетарного механизма, содержащего четыре центральных звена: три колеса – 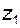 ,
, 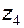 ,
, 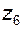 и водило H. Однако водило в этой схеме не является основным звеном, так как оно не может быть нагружено никаким внешним вращающим моментом, поэтому данный механизм отнесен к типу 3K (т.е. символ H в обозначение типа механизма не входит).
и водило H. Однако водило в этой схеме не является основным звеном, так как оно не может быть нагружено никаким внешним вращающим моментом, поэтому данный механизм отнесен к типу 3K (т.е. символ H в обозначение типа механизма не входит).
Найдем передаточное отношение 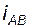 этого механизма:
этого механизма:
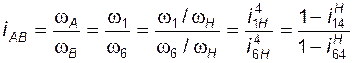 . (3.16)
. (3.16)
Обращенный механизм для данной схемы представляет собой разветвляющуюся рядовую кинематическую цепь, каждой из двух ее ветвей соответствует свое передаточное отношение:
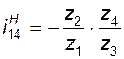 ;
; 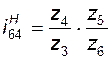 . (3.17)
. (3.17)
После очевидных подстановок получаем
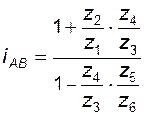 . (3.18)
. (3.18)
3.3. Кинематика комбинированных механизмов
с последовательным соединением ступеней
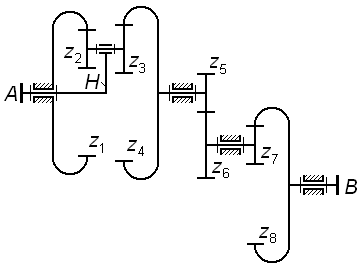 |
| Рис. 3.10 |
На рис. 3.10 показан комбинированный механизм, который содержит:
– планетарную ступень типа 2KH (редуктор Давида с двумя внутренними зацеплениями), включающий в себя водило H, сателлиты 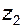 и
и 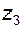 , центральные колеса
, центральные колеса 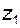 и
и 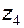 ;
;
– рядовую ступень внешнего зацепления 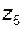 и
и 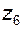 ;
;
– рядовую ступень внутреннего зацепления 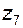 и
и 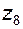 .
.
Найдем передаточное отношение механизма: принимая во внимание, что 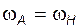 ,
, 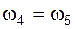 ,
, 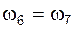 и
и 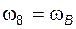 , запишем
, запишем
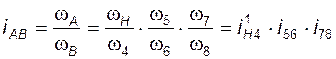 ; (3.19)
; (3.19)
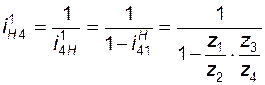 ; (3.20)
; (3.20)
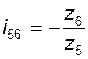 ;
; 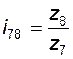 ; (3.21)
; (3.21)
после необходимых подстановок получаем
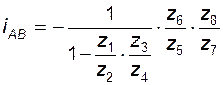 . (3.22)
. (3.22)
Как видно из (3.19), при последовательном соединении ступеней общее передаточное отношение комбинированного механизма равно произведению передаточных отношений всех ступеней. Единственная трудность при анализе таких механизмов – корректно выделить планетарные ступени и для них написать правильные формулы передаточных отношений.
