Напряжения и расчет на прочность

Рассчитать стержень круглого поперечного сечения на прочность (рис. 5.18). Расчет на прочность выполняется с использованием усло­вия прочности при кручении. Во-первых, необходимо расчетным путем определить максимальные касательные напряжения 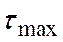, воз­никающие в опасном поперечном сечении. Этот расчет производит­ся по формуле:

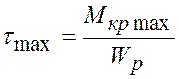. (5.25)

Как видно из формулы предварительно необходимо опре­делить максимальный крутящий момент 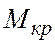, возникающий от дей­ствия внешней нагрузки. Крутящий момент 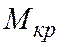характеризует уро­вень внутренних сил, возникающих в стержне и уравновешивающих внешнюю нагрузку. Чем больше значение 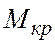, тем выше уровень внутренних сил, возникающих в стержне. Следовательно, прочность стержня будет определять то поперечное сечение стержня, в котором крутящий момент 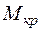имеет максимальное значение 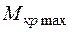. Размерность крутящего момента — кГ· см, кГ·м, Н·м, кН·ми т. д.

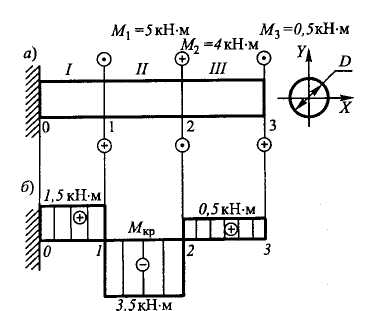
Рис. 5.18

Обратимся к рис. 5.18и подробно рассмотрим эпю­ру крутящих моментов ,возникающих в рассматри­ваемом стержне постоянно­го поперечного сечения. Как видно из эпюры на­ибольшие по величине кру­тящие моменты возникают в поперечных сечениях участ­ка II

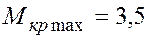кН·м.

Следовательно, опасноесечение определяющее прочность всего стержня, будет сечение участка II. Затем, после опреде­ления максимального значения крутящего момента, необходимо определить характеристику поперечного сечения, определяющую прочность круглого стержня при кручении, которая называется полярным моментом сопротивления и обозначается .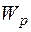

Рассмотрена часть задачи, а именно только определение мак­симальных касательных напряжений 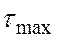, которые определяют про­чность стержня, но не дают ответа на вопрос, выдержит ли рассмат­риваемый стержень внешнюю нагрузку без разрушения или нет. Для решения поставленной задачи еще необходимо знать допуска­емые напряжения , в сравнении с которыми максимальных напря­жений 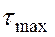и выносится решение о прочности или непрочности рассчитываемого вала. Определяется это с использованием условия прочности при кручении (5.25)

.

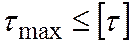Таким образом, путем сравнения максимальных напряжений, возникающих в опасном сечении стержня круглого поперечного сечения 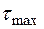с допускаемыми 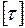и принимается решение о прочности стержня.

С использованием условия прочности возможно решение двух задач.

1. Первая задача носит название проверочной.

2. Вторая задача называется проектировочной.

Иногда решается так же задача определения предельно допусти­мой нагрузки на элементы конструкции. Рассмотрим решение пер­вых двух на конкретных примерах.

Проверочная задача. При постановке и решении проверочной задачи ищется ответ на вопрос, выдержит конкретный стержень круглого поперечного сечения, конкретного диаметра D, выполнен­ный из конкретного материала приложенную к нему внешнюю нагрузку без разрушения или нет. Проиллюстрируем изложенное на примерах.

Дано: 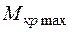=3,5 кН·м=3,5∙10³Н·м; D= 0,02 м; 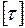=100МПа =100∙10⁶Па.

Вопрос: Условие прочности выполняется или нет?

Решение.

1. Определим полярный момент сопротивления:

.

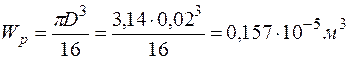2. Определим максимальные касательные напряжения:

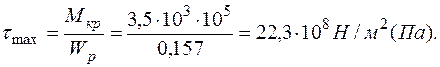
3.Воспользуемся условием прочности:

.

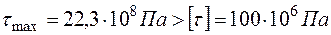Проведенные вычисления показывают, что условие прочности не выполняется, а именно, максимальные касательные напряжения в опасном сечении 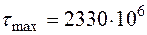Па, значительно больше допуска­емых напряжений 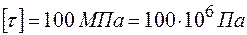, следовательно рас­считываемый стержень (вал) разрушится.

Ответ: Условие прочности не выполняется.

Проектировочная задача. Рассмотрим другую задачу, возника­ющую при кручении стержня круглого поперечного сечения.

Необходимо расчетным путем определить D— диаметр попе­речного сечения стержня, воспринимающего заданную внешнюю нагрузку без разрушения. Так же как и проверочная задача, проек­тировочная решается с использованием известного условия прочно­сти (5.25).

Сначала подставим в условие прочности вместо 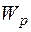его выраже­ние, т. е.

,

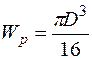в результате чего получим:

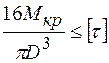
Решив полученное неравенство относительно D, мы фактически решим, в общем виде, поставленную задачу:

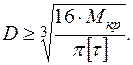
Совершенно очевидно, что полученная формула позволяет вычи­слить D— наименьший диаметр поперечного сечения стержня, удо­влетворяющий условию прочности.

Определить наименьший диаметр вала D. Дано: 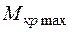= 3,5кНм=3,5·10³Нм; 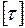= 100 МПа=100·10⁶Па.

Решение. Поставленная задача решается в одно действие, а именно:

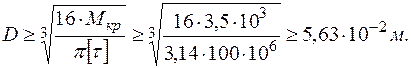
Следовательно, стержень постоянного поперечного сечения диа­метром D = 5,63·10^-2м выдержит приложенную к нему заданную внешнюю нагрузку без разрушения.

Вал трубчатого сечения. Однако стержень круглого сплошного поперечного сечения не является идеальным при работе на кручение. Из рис. 3, б видно, что касательные напряжения в поперечном сечении изменяются от нуля, в центре тяжести, до , на границе круга. Следовательно, основная доля внутренних сил приходится на ту часть сечения, которая наиболее удалена от центра тяжести, а центральная часть сечения практически не работает, и материал израсходован нерационально.

Рассмотрим круглое поперечное сечение, выполненное в виде полой трубы (рис. 5.19). Полярный момент инерции для трубы вычисляется по формуле:

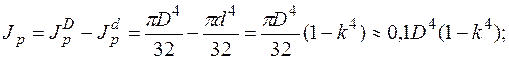
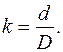
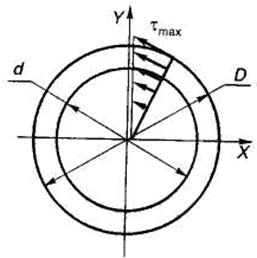
Рис. 5.19

Полярный момент сопротивления 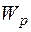полой трубы определяется формулой

.

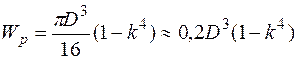Условие прочности для стержня трубчатого поперечного сечения:

.

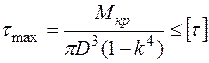Решив полученное неравенство относительно D, получим

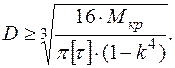
Расчет на жесткость при круче­нии. Рассмотрим расчет стержня круглого поперечного сечения на же­сткость (рис. 5.19) на следующем примере.

Определить максимальный угол закручивания 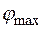стержня круглого поперечного сечения.

Дано: 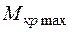=7 кНм=7·10³Нм; D = 0,04 м; G=8·10⁴МПа =8·10¹⁰ Па;l=7м.

Решение. Строим эпюру крутящих моментов стержня от действия заданной внешней нагрузки (рис. 5.20, б).

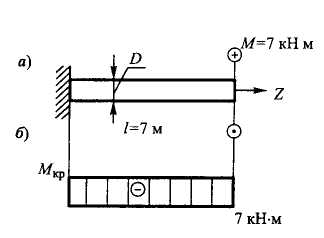
Рис. 5.20

Определяем максимальный угол закручивания стержня

,

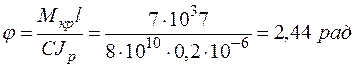где

.

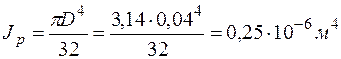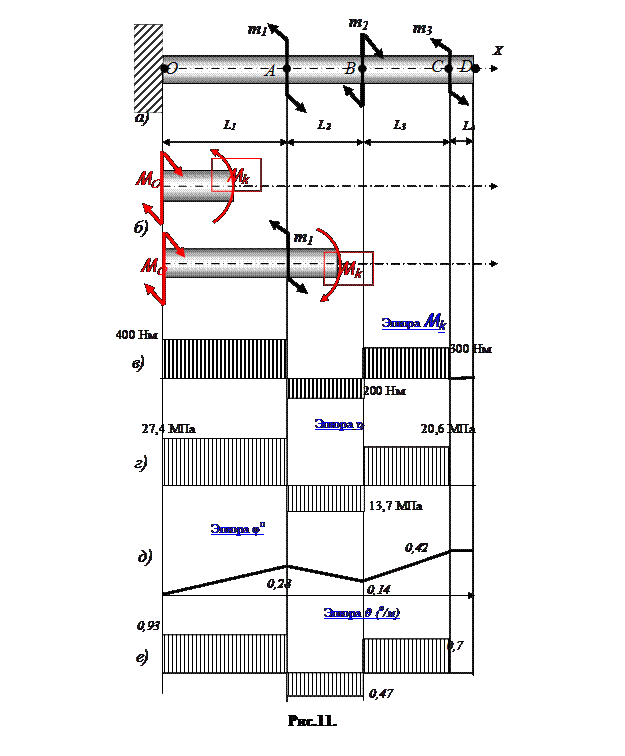
ЗАДАЧА (домашняя)

Стальной брус круглого поперечного сечения нагружен системой внешних моментов (рис.11.а), а именно: , , .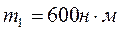

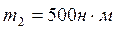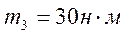Размеры отдельных частей бруса: , , , .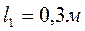

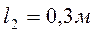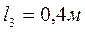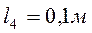Механические свойства материала бруса:

, , .

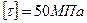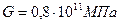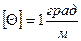Требуется:

1. Построить эпюру крутящих моментов.

2. Определить диаметр бруса из расчёта на прочность и жёсткость.

3. Построить эпюру максимальных касательных напряжений.

4. Построить эпюры абсолютных и относительных углов поворота поперечных сечений.

Решение:

1. Из условия равновесия 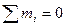находим реактивный момент в защемлени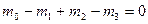и: или .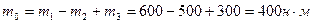

Методом сечений определяем крутящие моменты в произвольном сечении каждого из участков бруса (рис.11.б).

Участок I: ; .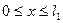

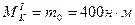Участок II: ; .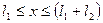

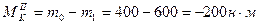Участок III: ;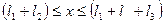

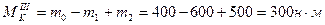
Крутящий момент на участке III проще получить, рассматривая правую часть бруса: .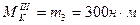

Участок IV: ; .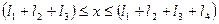

По полученным данным построена эпюра крутящих моментов (рис12.в), из которой видно, что участок I бруса является наиболее опасным, так как в поперечных сечениях этого участка крутящий момент имеет максимальное значение: .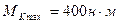

2. Определяем диаметр бруса круглого сечения:

А) из условия прочности ,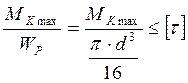

тогда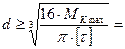

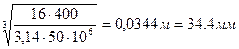
Б) из условия жёсткости ,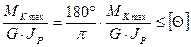

где ,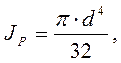

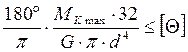тогда .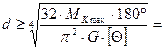

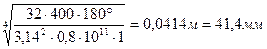Окончательно принимаем большее из полученных значений с округлением в большую сторону, .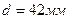

При этом, ,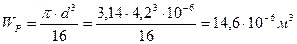

.

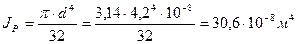3. Вычисляем величины наибольших касательных напряжений, возникающих в поперечных сечениях отдельных участков бруса:

,

,

.

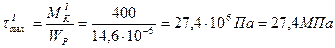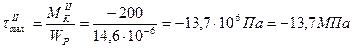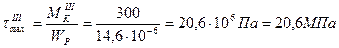Знак касательного напряжения не имеет физического смысла и здесь указан лишь для достижения соответствия эпюр касательных напряжений и крутящих моментов (рис.11.г).

4. Углы поворота граничных сечений участков относительно неподвижного сечения О определяем по формуле .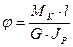

В пределах между границами участков величины углов поворота изменяются по линейному закону.

Жёсткость поперечного сечения рассчитываемого бруса

.

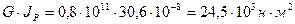Угол поворота сечения А относительно сечения О

.

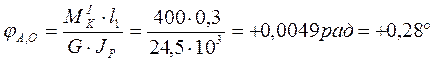Угол поворота сечения В относительно сечения А

.

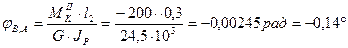Угол поворота сечения В относительно сечения О

.

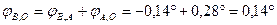Аналогично, ,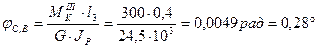

, , .

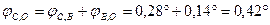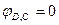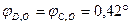Эпюра 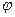дана на рис.11.д.

Определяем относительные углы закручивания на отдельных участках бруса:

, ,

, .

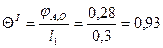
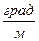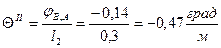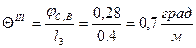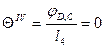Эпюра построена на рис.11.е.