Пример выполнения заданий. Построение первой формулы Ньютона в пакете MATHCAD

Построение первой формулы Ньютона в пакете MATHCAD.

Пример функции для построения матрицы конечных разностей:

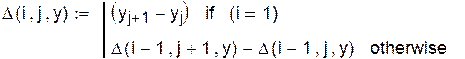
Первая формула Ньютона может иметь вид

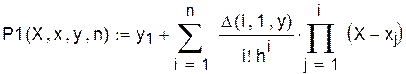
Формулу Гаусса можно реализовать следующим образом:

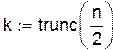
где x, y – табличные значения; X – точка интерполяции; n – количество узловых точек.

Пример программ для вычислений по первой формуле Ньютона в MATLAB.

X,Y – табличные значения; x – точка интерполяции; n – количество узловых точек.

function res = Nuton1(x,X,Y,n)

res=Y(1);

% определение шага таблицы

H=X(2)-X(1);

for i=1:n

% построение матрицы конечных разностей

konrazn=diff(Y,i);

konrazn=konrazn(1);

% вычисление факториала

fact=prod(1:i);

% вычисление (x-x₀)(x-x₁)...(x-x_n-1)

Mult=1;

for j=1:i

Mult=Mult*(x-X(j));

end;

res=res+(konrazn/(fact * H^i))*Mult;

end;

res

return

Функция EvalNuton.mвычисляет значения указанного полинома в заданном множестве точек:

function yy = EvalNuton(X,Y,xx,formNumber)

n=length(X)-1;

if (formNumber==1)

for i=1:length(xx);

yy(i)=Nuton1(xx(i),X,Y,n);

end;

else

for i=1:length(xx);

yy(i)=Nuton2(xx(i),X,Y,n+1);

end;

end;

return

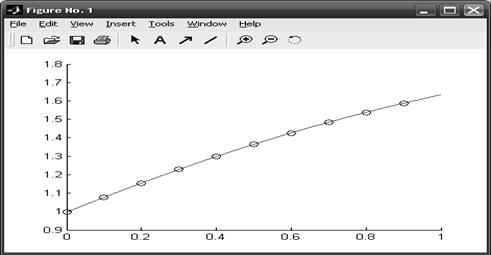
Пример вызова функций и построения графика:

>> x = [0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]

>> y = [0.99602 1.07670 1.15402 1.22777 1.29776 1.36386 1.42592 1.48384 1.53751 1.58688]

>> EvalNuton(x,y,0.04,1)

res =

1.0287

>> EvalNuton(x,y,0.89,2)

res =

1.5821

>> xx=linspace(0,1,1000)

>> yy=EvalNuton(x,y,xx,1)

>> figure('Color','w')

>> hold on

>> plot(xx,yy,'r')

>> plot(x,y,'bo')

Обратное интерполирование с помощью полинома Ньютона в пакете MATHCAD.

Используется первая формула Ньютона, которая записана с помощью функции пользователя. Для реализации метода итераций организован программный блок, выходными параметрами которого являются искомое значение аргумента и необходимое количество итераций:

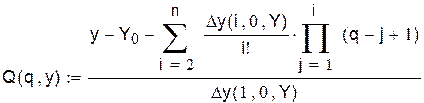
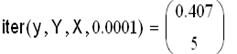
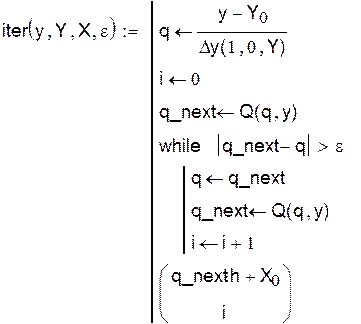
Решение задачи обратного интерполирования

С помощью полинома Ньютона в пакете MATLAB.

Res – функция для решения по методу итераций. Эта функция вызывает функцию Q(q,y,Y,n), которая определяет первую интерполяционную формулу Ньютона для метода обратной интерполяции:

function res=iter(y,Y,X,eps)

h = X(2)-X(1);

n = length(X);

konrazn=diff(Y,1);

konrazn=konrazn(1);

q = (y - Y(1))/konrazn;

q_next = Q(q,y,Y,n);

while abs(q_next-q)>eps

q=q_next;

q_next = Q(q,y,Y,n);

end;

res = q_next*h+X(1);

return

% функция Q(q,y,Y,n):

function res=Q(q,y,Y,n)

sum = 0;

for i=2:n-1

% вычисление конечной разности

konrazn=diff(Y,i);

konrazn=konrazn(1);

% вычисление факториала

fact=prod(1:i);

% вычисляем (x-y₀)(x-y₁)...(x-y_n-1)

Mult=1;

for j=1:i

Mult=Mult*(q-j+1);

end;

sum=sum+(konrazn/(fact))*Mult;

end;

konrazn=diff(Y,1);

konrazn=konrazn(1);

res = (y-Y(1)-sum)/konrazn;

return

Пример вызова функций:

> > x = [0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]

>> y= [0.99602 1.07670 1.15402 1.22777 1.29776 1.36386 1.42592 1.48384 1.53751 1.58688]

>> iter(1.36386,y,x,0.001)

ans =

0.5000

>> iter(1.30254,y,x,0.001)

ans =

0.4070

Варианты заданий

Номер варианта	Функция	Точки интерполяции		Номер варианта	Функция	Точки интерполяции
	А			А
	Б			Г
	В			Б
	А			Д
	Г			Г
	В			А
	Б			Д
	Д			Б
	А			В
	Г			Г
	В			Б
	Д			А
	Б			В
	В			Г
	Д			Д

Точки интерполяции

№ п/п				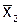		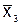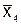№ п/п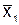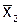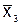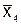
	0,01	0,52	0,89	0,02			0,04	0,54	0,89	0,86
	0,04	0,46	0,87	0,88			0,03	0,43	0,86	0,02
	0,05	0,41	0,86	0,03			0,02	0,43	0,87	0,86
	0,02	0,32	0,89	0,87			0,03	0,42	0,88	0,02
	0,01	0,45	0,88	0,03			0,05	0,43	0,87	0,89

Уравнения для решения задачи нахождения корня методом обратного интерполирования взять из лабораторной работы № 2.