Фиктивные переменные во множественной регрессии

До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. В отечественной литературе можно встретить термин «структурные переменные».

Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид:

,

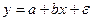где 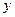– количество потребляемого кофе; 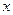– цена.

Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: 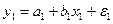и женского пола: .

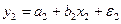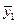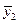Различия в потреблении кофе проявятся в различии средних и . Вместе с тем сила влияния 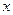на 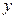может быть одинаковой, т. е. 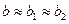. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения 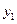и 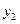и вводя фиктивные переменные, можно прийти к следующему выражению:

,

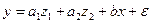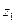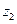где и – фиктивные переменные, принимающие значения:

.

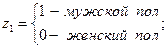
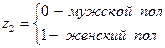В общем уравнении регрессии зависимая переменная у рассматривается как функция не только цены, но и пола ( 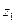, 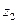). Переменная 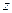рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда 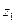=1, то 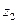=0 и, наоборот, при 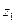=0 переменная 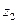=1.

Для лиц мужского пола, когда 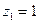и 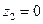, объединенное уравнение регрессии составит: 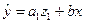, а для лиц женского пола, когда 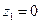и 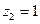, 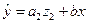. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: 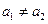. Параметр 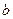является общим для всей совокупности лиц, как для мужчин, так и для женщин.

Следует иметь в виду, что при введении фиктивных переменных 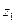и 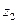в модель 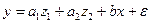применение МНК для оценивания параметров 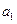и 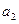приведет к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т. е. yравнение примет вид

.

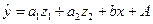Ранее говорилось только о качественном факторе, который имел только два состояния, которым и соответствовали обозначения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.

В отдельных случаях может оказаться необходимым введение двух и более групп фиктивных переменных, т. е. двух и более качественных факторов, каждый из которых может иметь несколько градаций. Например, при изучении потребления некоторого товара наряду с факторами, имеющими количественное выражение (цена, доход на одного члена семьи, цена на взаимозаменяемые товары и др.), учитываются и качественные факторы. С их помощью оцениваются различия в потреблении отдельных социальных групп населения, дифференциация в потреблении по полу, национальному составу и др. При построении такой модели из каждой группы фиктивных переменных следует исключить по одной переменной. Так, если модель будет включать три социальные группы, три возрастные категории и ряд экономических переменных, то она примет вид:

,

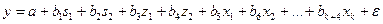где 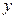– потребление;

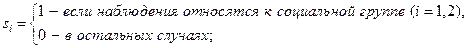
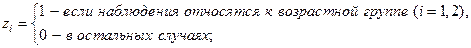
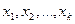– экономические (количественные) переменные.

Фиктивные переменные широко используются для оценки сезонных различий в потреблении. Учет сезонного фактора при построении динамических моделей рассмотрен позже.

Фиктивные переменные могут вводиться не только в линейные, но и в нелинейные модели, приводимые путем преобразований к линейному виду.

Включение в модель фиктивных переменных может иметь цель отразить в модели неоднородность совокупности. Однако нельзя рассматривать фиктивные переменные как панацею при применении методов регрессии к неоднородным данным.

До сих пор мы рассматривали фиктивные переменные как факторы, которые используются в регрессионной модели наряду с количественными переменными. Вместе с тем возможна регрессия только на фиктивных переменных. Например, изучается дифференциация заработной платы рабочих высокой квалификации по регионам страны. Модель заработной платы может иметь вид:

,

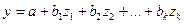где 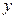– средняя заработная плата рабочих высокой квалификации по отдельным предприятиям;

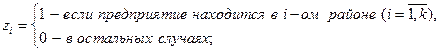
Поскольку последний район, указанный в модели, обозначен 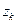, то в исследование включено 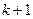район.

Ввиду того, что факторы данной регрессионной модели выражены как дихотомические признаки, параметры модели имеют свою специфику по сравнению с традиционной их интерпретацией. Параметр 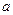представляет собой среднее значение результативного признака для базовой группы 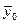. Параметр 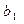характеризует разность средних уровней результативного признака для группы 1 и базовой группы 0. Соответственно параметр 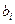представляет собой разность между 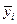и 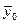. Иными словами, коэффициенты при 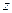отражают величину эффекта соответствующей группы фактора 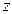. Рассмотрим применение данной модели на следующем условном примере.