Дифференциальное уравнение прямого изгиба призматического стержня

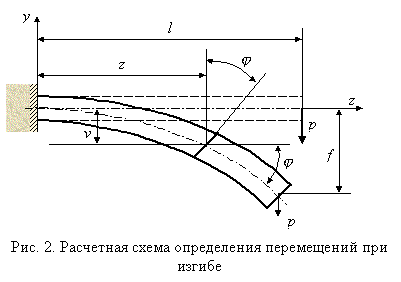
Определено, что мерой деформации призматического стержня при прямом чистом изгибе является кривизна нейтрального слоя. Можно показать, что с достаточной для инженерных расчетов точностью этим тезисом можно пользоваться и в случае прямого поперечного изгиба стержня. Однако для практических целей кроме кривизны 1/r необходимо определить вертикальные перемещения центров тяжести отдельных поперечных сечений - прогибов балки v, а иногда и углы поворота этих сечений j (рис. 2). Вследствие гипотезы плоских сечений угол поворота сечения (j оказывается равным углу наклона касательной к изогнутой оси балки, который в силу малости

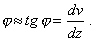
Тогда возникает геометрическая задача: составить уравнение для функции прогиба 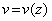, зная закон изменения ее кривизны.

Воспользуемся известным из дифференциальной геометрии выражением для кривизны в прямоугольных декартовых координатах:

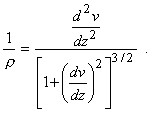
16 Напряжения и деформации при кручении призматических стержней кругового поперечного сечения

Ключевые слова: чистый сдвиг, жесткость сечения при кручении, угол закручивания, вал, прочность, жесткость.

Кручением называется такой вид деформации, при котором в поперечном сечении стержня возникает лишь один силовой фактор - крутящий момент М_z. Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oz. Нормальные силы, параллельные оси Oz, вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил - касательные напряжения t_xz и t_yz) М_z связывает вытекающее из его определения уравнение равновесия статики (рис. 1)

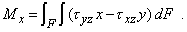
Условимся считать M_z положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (см. рис. 2). Это правило проиллюстрировано на рис. 1 и в указанном соотношении, где крутящий момент М_z принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси О_z.

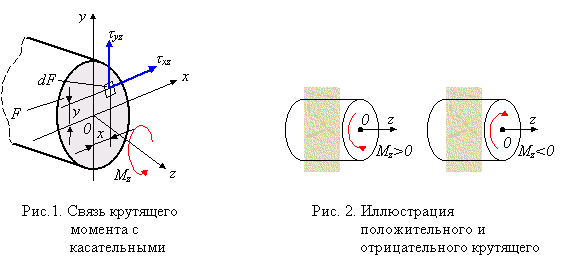
Рассмотрим кручение призматических стержней кругового поперечного сечения. Исследование деформаций упругого стержня с нанесенной на его поверхности ортогональной сеткой рисок (рис. 3) позволяет сформулировать следующие предпосылки теории кручения этого стержня:

1. поперечные сечения остаются плоскими (выполняется гипотеза Бернулли);
2. расстояния между поперечными сечениями не изменяются, следовательно e_z=0;
3. контуры поперечных сечений и их радиусы не деформируются. Это означает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня Оz. Отсюда следует, что любые деформации в плоскости пластинки равны нулю, в том числе и e_x = e_y =0;
4. материал стержня подчиняется закону Гука. Учитывая, что e_x =e_y = e_z =0, из обобщенного закона Гука в форме получаем e_x =s_y = s_z =0. Это означает, что в поперечных сечениях, стержня возникают лишь касательные напряжения t, а вследствие закона парности касательных напряжений, равные им напряжения действуют и в сопряженных продольных сечениях. Следовательно напряженное состояние стержня - чистый сдвиг.

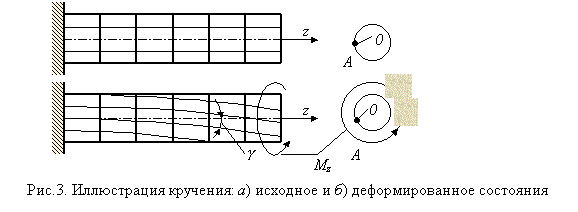
Выведем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения. Как видно, поворот правого торцевого сечения относительно неподвижного левого на угол j (назовем его углом закручивания стержня) вызывает поворот продольных волокон на угол g (угол сдвига), поскольку на величину g искажаются углы ортогональной сетки продольных и поперечных рисок модели.

Двумя смежными сечениями вырежем элемент стержня длиной dz и, поскольку нас интересуют деформации элемента, левое сечение его будем считать неподвижным (рис. 4). При повороте правого сечения на угол dj в соответствии с гипотезой о недеформируемости радиусов, правый конец волокна АВ (отстоящий от оси элемента на величину полярного радиуса r) будет перемещаться по дуге BB₁, вызывая поворот волокна на угол сдвига

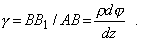
Обратим внимание на то, что в соответствии с рис. 4 и рис. 5, а сдвиг g и связанное с ним касательное напряжение t перпендикулярны радиусу r. Определим t, воспользовавшись законом Гука для чистого сдвига

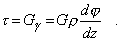
(1)

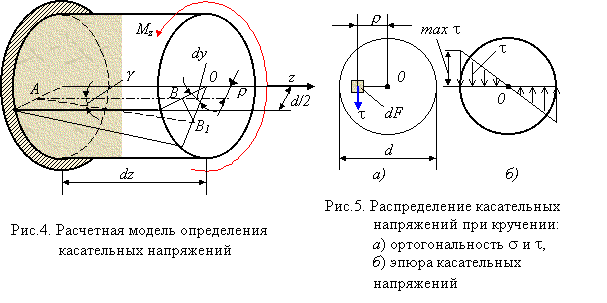
Здесь dj /dz - погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 5, a)

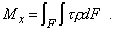
(2)

Подставляя (1) в (2) и учитывая, что

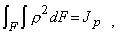
где J_p - полярный момент инерции поперечного сечения (для круга с диаметром d J_p=p⁴/32), получаем

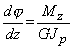
(3)

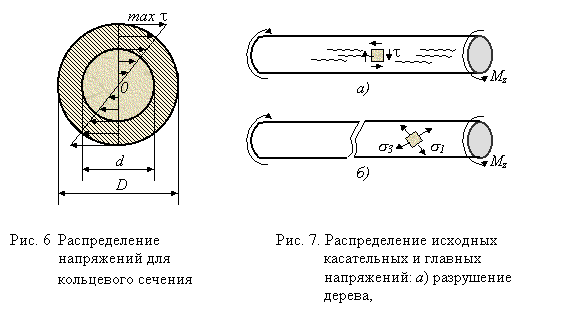
Подставляя выражение (3) в (1), получаем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения

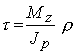
(4)

Как видно из (4), сдвиги и касательные напряжения пропорциональны расстояний от оси стержня. Обратим внимание на структурные аналогии формул для нормальных напряжений чистого изгиба и касательных напряжений кручения.

Мерой деформации стержня при кручении является погонный угол закручивания стержня, определяемый по (3). Поскольку величина DJ_p стоит в знаменателе формулы и при заданной нагрузке (M_z через нее выражается) dj /dz тем меньше, чем больше DJ_p, последнюю называют жесткостью поперечного сечения при кручении.

Пользуясь (3) для определения угла закручивания элемента длиной dz

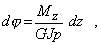
найдем полный угол закручивания стержня длиной l

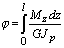
(5)

В случае, если по длине стержня М_z и DJ_p постоянны, получаем

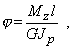
когда эти величины кусочно-постоянны, то:

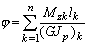
(6)

Отметим, что полученные формулы по структуре аналогичны формулам для деформаций при растяжении стержня.

Наибольшие касательные напряжения возникают у внешней поверхности стержня, т. е. при r_max=d/2

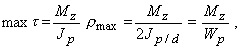
где W_р - момент сопротивления при кручении или полярный момент сопротивления

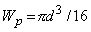
Полярный момент сопротивления, стоящий в знаменателе для максимальных касательных напряжений, очевидно, является геометрической характеристикой сечения, а условие прочности стержня при кручении принимает вид

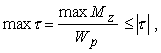
(7)

где [t] - допускаемое напряжение на кручение.

Как показали эксперименты и точное решение этой задачи в теории упругости, все гипотезы, сформулированные ранее для стержня со сплошным круговым сечением, остаются справедливыми и для стержня кольцевого поперечного сечения (рис. 6). Поэтому все выведенные ранее формулы пригодны для расчета стержня кольцевого сечения с той лишь разницей, что полярный момент инерции определяется как разность моментов инерции кругов с диаметрами D и d

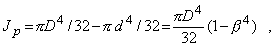
где b=d/D, а момент сопротивления определяется по формуле

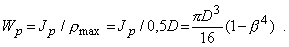
Учитывая линейный характер изменения касательных напряжений по радиусу (рис. 6) и связанное с этим лучшее использование материала, кольцевое сечение следует признать наиболее рациональным при кручении стержня. Коэффициент использования материала тем выше, чем меньше относительная толщина трубы.

Как отмечено ранее, напряженное состояние при кручении стержня - чистый сдвиг, являющийся частным случаем плоского напряженного состояния. На площадках, совпадающих с плоскостью поперечного сечения и на парных им площадках продольных сечений возникают экстремальные касательные напряжения max-min t, а главные напряжения s_1,3 = ± t действуют на площадках, наклоненных .коси стержня под углами ±45°; главное напряжение s₂ = 0.

Особенности напряженного состояния при кручении нашли отражение в характере разрушения стержней. Так, разрушение стержня из дерева, плохо работающего на скалывание вдоль волокон, происходит от продольных трещин (рис. 7, a). Разрушение стержня из хрупкого металла (например, чугуна) происходит по винтовой линии, наклоненной к образующим под углом 45°, т. е. по траектории главного напряжения s₃ (рис. 7,б).

Расчет валов

Рассмотрим расчет вала на прочность и жесткость. Пусть известна мощность W (кВт), передаваемая вращающимся с заданным числом оборотов в минуту (n) валом от источника мощности (например, двигателя) к ее потребителю (например, станку), а момент m, передаваемый валом, требуется найти, так как численно равный этому моменту крутящий момент необходим для расчета вала.

Если число оборотов вала в минуту п и соответствующая угловая скорость w(с^-1) постоянны, а Ф - угол поворота вала в данный момент времени t, то работа вращательного движения А=mФ. Тогда передаваемая валом мощность будет равна

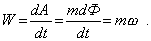
Отсюда

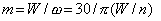кНм

где учтено, что .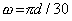

Если мощность подается на вал через ведущий шкив, а раздается потребителям через несколько ведомых шкивов, то соответственно определяются моменты на шкивах, а затем строится эпюра крутящих моментов. Расчет вала на прочность и жесткость ведется, очевидно, по max M_z.

Определение диаметра вала из условия прочности. Условие прочности при кручении вала имеет вид (7), где допускаемые напряжения [t] принимаются пониженными по сравнению с допускаемыми напряжениями обычного статического расчета в связи с необходимостью учета наличия концентраторов напряжений (например, шпоночных канавок), переменного характера нагрузки и наличия наряду с кручением и изгиба вала.

Требуемое значение W_p=d^з/16 получаем из условия (7), принимая в нем знак равенства

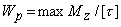
откуда получаем формулу для диаметра вала кругового сечения

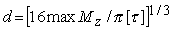
Определение диаметра вала из условия жесткости. Условие жесткости состоит в наложении ограничения на погонный угол закручивания вала 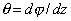, так как недостаточно жесткие валы не обеспечивают устойчивой передачи мощности и подвержены сильным колебаниям:

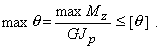
Тогда, учитывая, что J_p=pd⁴/32, для диаметра вала из условия жесткости имеем

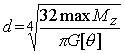
Аналогично проводятся расчеты и для вала кольцевого поперечного сечения.

17 Сложные виды деформации

Ключевые слова: косой изгиб, внутреннее сжатие-растяжение, условия прочности.