Анализ точности в методе наименьших квадратов в линейном случае

При использовании различных методов наименьших квадратов возникает задача анализа точности полученных алгоритмов

Для этого введем понятие ошибок оценок

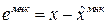
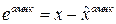
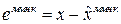
Рассмотрим ошибку для МНК

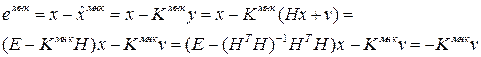
Аналогичным образом оприделяется ошибка для ОМНК

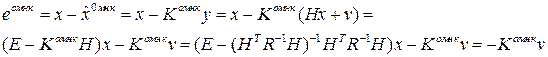
Для модифицированного ММНК уравнение в ошибках примет вид

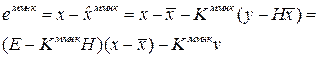
Введем предположение, что ошибки измерений являются центрированными и для них известна матрица ковариаций

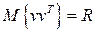
В этом случае действительные ковариационные матрицы ошибок оценок будут равны

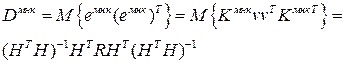
Аналогичным образом

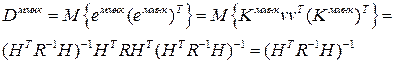
Для расчета ковариационной матрицы ошибки оценки в ММНК потребуется предположение о коррелированности ошибок измерений и ошибок априорной информации. При отсутствии корреляции получим

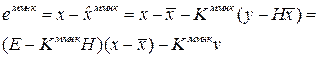
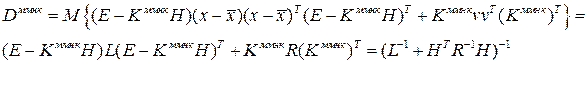
Можно показать, что при грамотном выборе матриц и справедлива следующая цепочка неравенств

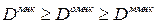
Рекуррентная схема наименьших квадратов

Представим 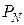в виде

,

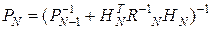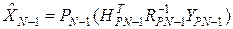-оценка после обработки 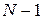измерений. Тогда

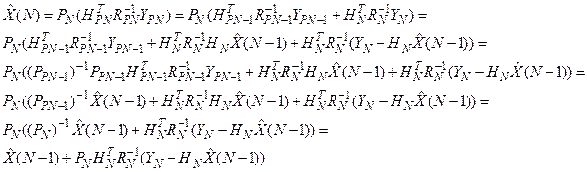
т.е. получено рекуррентное выражение для оценки

Заметим, что это выражение может быть приведено к виду,

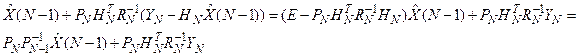
что также широко используется при анализе схем обработки измерений

Частный случай обработки прямых равноточных измерений

Применим полученные результаты к обработке прямых измерений, когда фундаментальная система уравнений имеет вид

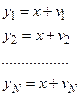
В этом случае вектор измерений , матрица измерений и вектор ошибок измерений имеют вид

, ,

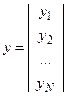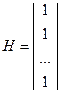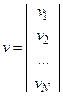
и фундаментальная система измерений может быть записана как

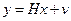
Используем МНК

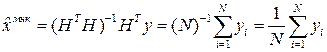
Если использовать равноточные измерения с дисперсией 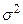, то дисперсия ошибки оценки будет определяться выражением

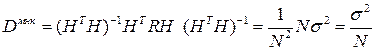
Метод максимального правдоподобия

Рассмотрим теперь метод максимального правдоподобия. В рамках этого метода рассматривается совместная плотность 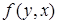, где в общем случае 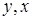векторные величины. В случае независимых величин совместную плотность можно записать как

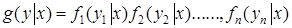
Эта плотность получила название функции правдоподобия. Те значения 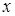,при которых функция правдоподобия достигает максимума получили название оценок максимума правдоподобия. Оказалось, что эти оценки при достаточно общих предположениях являются асимптотически несмещенными, асимптотически нормальными и асимптотически эффективными.

Для упрощения вычислительной процедуры обычно максимизируют не саму функцию правдоподобия 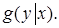, а ее логарифм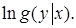

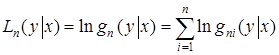
при этом решение задачи сводится к решению уравнений

.
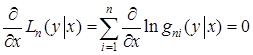