Задачи к лабораторной работе
ЛАБОРАТОРНАЯ РАБОТА № 1
ГРУППЫ И ИХ ПОДГРУППЫ
Вопросы для самоконтроля
1. Дать определение группы с произвольной бинарной алгебраической операцией.
2. Как задать группу?
3. Что значит аддитивная (мультипликативная) группа?
4. Сколько единиц (нулей) в мультипликативной (аддитивной) группе?
5. Сколько противоположных (обратных) имеет элемент в аддитивной (мультипликативной) группе?
6. Что является в аддитивной группе аналогом степени элемента?
7. Дать определение изоморфизма для (мультипликативных) аддитивных групп.
8. Дать определение изоморфизма, когда одна группа аддитивна, а другая - мультипликативная.
9. Является ли изоморфизм отношением эквивалентности?
10. Является ли мультипликативная группа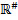 
подгруппой аддитивной группы 
?
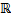11. Сформулировать критерий для подгрупп аддитивных групп.
12. Дать определение порядка элемента в аддитивной группе.
13. Конечны ли порядки элементов в конечной группе?
14. Могут ли в группе все элементы иметь бесконечный порядок?
15. Будут ли равны порядки |x| и |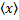 
|, где x - элемент группы?
16. В аддитивных группах определить сумму подмножеств и смежный класс.
17. Записать тождество Дедекинда для подгрупп K, L,M, где L ⊆ M.
18. Сформулировать свойства смежных классов в аддитивной записи.
19. Что называется индексом подгруппы?
20. Пусть A и B нормальные подгруппы группы G, A∩B = E. Доказать, что ab = ba для любых a ∈ A и b ∈ B.
Задачи к лабораторной работе
1. Определена ли операция на множестве? Будут ли они группами?
1.1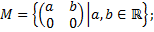 
1.2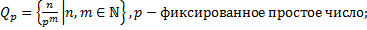 
1.3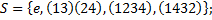 
1.4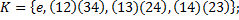 
1.5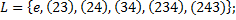 
2. Будет ли множество H подгруппой группы GL(n, )?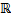
2.1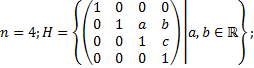 
2.2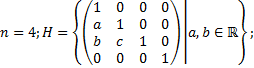 
2.3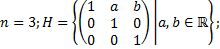 
2.4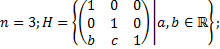 
2.5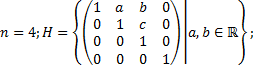 
3. Найти все элементы подгруппы M группы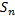 
и индекс подгруппы M в группе .
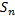3.1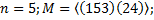 
3.2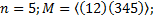 
3.3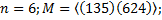 
3.4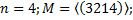 
3.5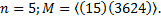 
4. Найти порядок элемента g, принадлежащего мультипликативной группе G. Вычислить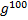 
.
4.1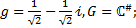 
4.2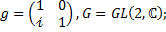 
4.3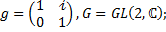 
4.4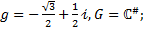 
4.5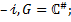 
5. Пусть A и B подгруппы группы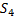 
. Будет ли подгруппой произведение AB? Найти число элементов множества AB.
5.1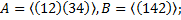 
5.2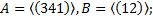 
5.3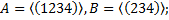 
5.4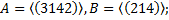 
5.5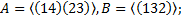 
6. Составить таблицу сложения для факторгруппы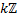 
по подгруппе 
.
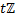6.1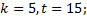 
6.2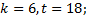 
6.3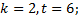 
6.4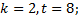 
6.5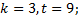 
ЛАБОРАТОРНАЯ РАБОТА № 2
ГОМОМОРФИЗМЫ И
ПРОИЗВЕДЕНИЯ ПОДГРУПП
Вопросы для самоконтроля
1. Дать определение гомоморфизма аддитивной группы в мультипликативную.
2. Будет ли естественный гомоморфизм эпиморфизмом?
3. Будет ли изоморфизм естественным гомоморфизмом?
4. Укажите гомоморфизм, который не является ни мономорфизмом, ниэпиморфизмом.
5. Что называется нециклической группой?
6. Дать определение порядка элемента в аддитивной записи.
7. Показать, что аддитивная группа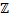 
целых чисел циклическая. Найти все образующие.
8. Найти все подгруппы группы целых чисел. Указать все образующие каждой подгруппы.
9. Найти все факторгруппы группы целых чисел. Указать все образующие каждой факторгруппы.
10. Рассмотреть аддитивную группу и дать определения разложения этой группы в прямую сумму своих подгрупп.
11. Чему равен порядок прямого произведения двух подгрупп?
12. Чему равен порядок элемента прямого произведения двух конечных групп?
Задачи к лабораторной работе
1. Пусть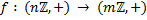 
такое отображение, что 
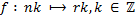, n, m, r - фиксированные натуральные числа. Доказать, что 
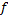- гомоморфизм. Найти ядро и образ 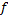. Будет ли 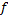мономорфизмом, эпиморфизмом, изоморфизмом?
1.1.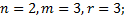 
1.2.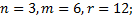 
1.3.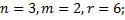 
1.4.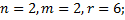 
1.5.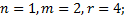 
2. Пусть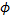 
- отображение группы 
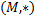в группу 
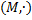. Будет ли 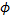гомоморфизмом? Если 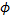гомоморфизм, то найти 
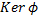и 
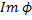. Будет ли 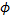мономорфизмом, эпиморфизмом, изоморфизмом?
2.1.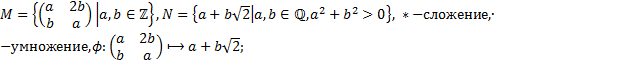 
2.2.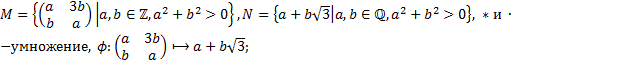 
2.3.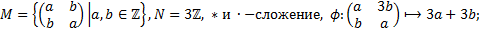 
2.4.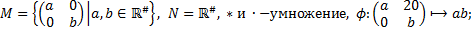 
2.5.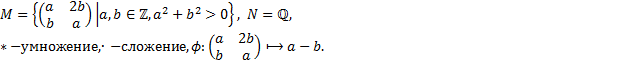 
3. Найти все элементы циклической подгруппы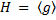 
группы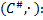 
3.1.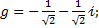 
3.2.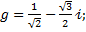 
3.3.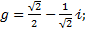 
3.4.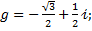 
3.5.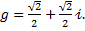 
4. Доказать, что порядки указанных элементов группы равны:
4.1.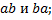 
4.2.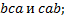 
4.3.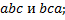 
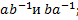
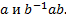
5. Разложить в прямую сумму циклическую группу порядка n:
5.1.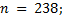 
5.2.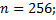 
5.3.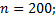 
5.4.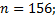 
5.5.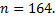 
6. Пусть H и K - подгруппы группы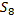 
. Существует ли в 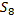подгруппа 
?
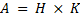6.1.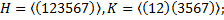 
6.2.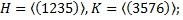 
6.3.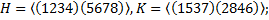 
6.4.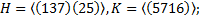 
6.5.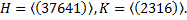 
ЛАБОРАТОРНАЯ РАБОТА № 3
ЛИНЕЙНЫЕ ГРУППЫ
Вопросы для самоконтроля
1. Критерий невырожденности матрицы.
2. Формула обратной матрицы.
3. Проверить, что множество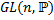 
невырожденных n×n-матриц над полем 
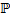образует группу. Является ли эта группа абелевой?
4. Проверить, что множество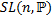 
невырожденных 
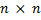- матриц с единичным определителем над полем 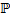образует группу. Является ли эта группа абелевой? Абелева ли группа 
?
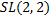5. Формулы порядков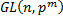 
и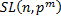 
с доказательством.
6. Доказать, что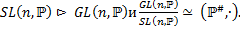 
7. Центр группы и его свойства.
8. Центры группы 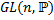и группы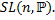 
9. Проективная общая и проективная специальная линейные группы и их порядки над конечными полями.
10. Разложение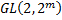 
в прямое произведение своих подгрупп.
11. Вложение группы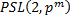 
в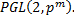 
12. Теорема о подгруппах группы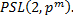 
Задание к лабораторной работе
1. Написать таблицу сложения и умножения для элементов поля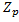 
. Указать каждому элементу противоположный и обратный:
1.1.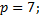 
1.2.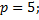 
1.3.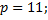 
1.4.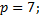
1.5.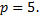 
2. Вычислить противоположную и обратную матрицы над полем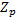 
для матрицы 
:
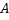2.1.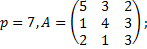 
2.2.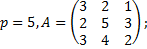 
2.3.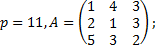 
2.4.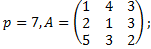 
2.5.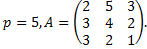 
3. Вычислить порядки групп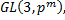 
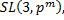
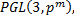
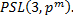Найти порядки центров групп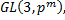 
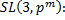
3.1.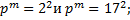 
3.2.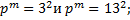 
3.3.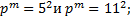 
3.4.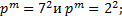 
3.5.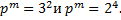 
4. Вычислить порядки и перечислить подгруппы группы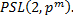
4.1.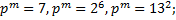 
4.2.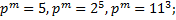 
4.3.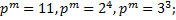 
4.4.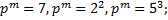 
4.5.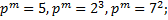 
ЛАБОРАТОРНАЯ РАБОТА № 4
ЦЕНТР И КОММУТАНТ
Вопросы для самоконтроля
1. Коммутатор элементов, коммутант группы.
2. Коммутант и факторгруппа, теорема Миллера.
3. Коммутант факторгруппы.
4. 
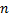–ый коммутант, разрешимые группы.
5. 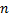–ый коммутант факторгруппы.
6. Примеры разрешимых групп.
7. Подгруппы и факторгруппы разрешимых групп.
8. Прямые произведения разрешимых групп.
9. Теорема о разрешимости группы с разрешимой нормальной подгруппой
и разрешимой факторгруппой по ней.
10. Центр группы и его свойства.
11. Абелевость группы с циклической факторгруппой по центру.