Ахождение кратчайшего пути в графе с помощью программы
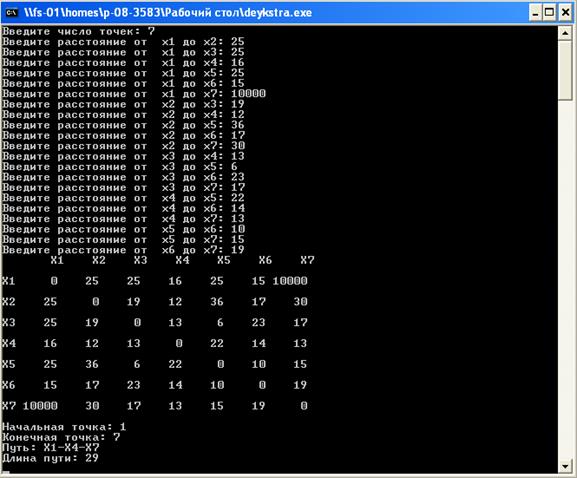
Начальная точка: 1
Конечная точка: 7
Путь: X1-X4-X7
Длина пути: 29
ЗАКЛЮЧЕНИЕ
В процессе создания курсовой работы задача была решена методом Дейкстры, в результате был получен ответ Путь: X1-X4-X7 Длина пути: 29, который был подтвержден программой.
Таким образом, в процессе создания курсовой работы была разработана программа, реализующая алгоритм Дейкстры в Microsoft Visual C++ 6.0. Её недостатком является примитивный пользовательский интерфейс. Это связано с тем, что программа работает в консольном режиме, не добавляющем к сложности языка сложность программного оконного интерфейса.
Деревья играют большую роль в биологической теории ветвящихся процессов. Для простоты мы рассмотрим только одну разновидность ветвящихся процессов – размножение бактерий. Предположим, что через определенный промежуток времени каждая бактерия либо делится на две новые, либо погибает. Тогда для потомства одной бактерии мы получим двоичное дерево.
Нас будет интересовать лишь один вопрос: в скольких случаях n-е поколение одной бактерии насчитывает ровно k потомков? Рекуррентное соотношение, обозначающее число необходимых случаев, известно в биологии под названием процесса Гальтона-Ватсона. Его можно рассматривать как частный случай многих общих формул.
СПИСОК ЛИТЕРАТУРЫ
1. Белов Теория Графов, Москва, «Наука»,1968.
2. Новые педагогические и информационные технологии Е.С.Полат, Москва, «Akademia» 1999 г.
3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.
4. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990.
5. Нефедов В.Н., Осипова В.А. Курс дискретной математики. – М.: Издательство МАИ, 1992.
6. Оре О. Теория графов. – М.: Наука, 1980.
7. Исмагилов Р.С., Калинкин А.В. Матеpиалы к пpактическим занятиям по куpсу: Дискpетная математика по теме: Алгоpитмы на гpафах. - М.: МГТУ, 1995
8. Смольяков Э.Р. Введение в теоpию гpафов. М.: МГТУ, 1992
9. Hечепуpенко М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях. - Hовосибиpск: Hаука, 1990
10. Романовский И.В. Алгоpитмы pешения экстpемальных задач. - М.: Hаука, 1977
11. Писсанецки С. Технология разреженных матриц. - М.: Мир, 1988
12. Севастьянов Б.А. Вероятностные модели. - М.: Наука, 1992
13. Бочаров П.П., Печинкин А.В. Теория вероятностей. - М.: Изд-во РУДН, 1994
ПРИЛОЖЕНИЕ
Текст программы определения кратчайшего пути в графе.
#include<iostream.h>
#include<string.h>
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#define word unsigned int
int i, j, n, p, xn, xk;
int flag[11];
word c[11][11], l[11];
char s[80], path[80][11];
int min(int n)
{int i, result;
for(i=0;i<n;i++)
if(!(flag[i])) result=i;
for(i=0;i<n;i++)
if((l[result]>l[i])&&(!flag[i])) result=i;
return result;}
word minim(word x, word y)
{if(x<y) return x;
return y;}
void main()
{cout<<"Vvedite kolichestvo tochek: ";
cin>>n;
for(i=0;i<n;i++)
for(j=0;j<n;j++) c[i][j]=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{cout<<"Vvedite rasstoyanie ot x"<<i+1<<" do x"<<j+1<<": ";
cin>>c[i][j];}
cout<<" ";
for(i=0;i<n;i++) cout<<" X"<<i+1;
cout<<endl<<endl;
for(i=0;i<n;i++)
{printf("X%d",i+1);
for(j=0;j<n;j++)
{printf("%6d",c[i][j]);
c[j][i]=c[i][j];}
printf("\n\n");}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(c[i][j]==0) c[i][j]=65535; //бесконечность
cout<<"Vvedite nachalnuy tochku: ";
cin>>xn;
cout<<"Vvedite konechnuy tochku: ";
cin>>xk;
xk--;
xn--;
if(xn==xk)
{cout<<"Nachalnaya I konechnaya tochki sovpadayt."<<endl;
getch();
return;}
for(i=0;i<n;i++)
{flag[i]=0;
l[i]=65535;}
l[xn]=0;
flag[xn]=1;
p=xn;
itoa(xn+1,s,10);
for(i=1;i<=n;i++)
{strcpy(path[i],"X");
strcat(path[i],s);}
do
{for(i=0;i<n;i++)
if((c[p][i]!=65535)&&(!flag[i])&&(i!=p))
{if(l[i]>l[p]+c[p][i])
{itoa(i+1,s,10);
strcpy(path[i+1],path[p+1]);
strcat(path[i+1],"-X");
strcat(path[i+1],s);}
l[i]=minim(l[i],l[p]+c[p][i]);}
p=min(n);
flag[p]=1;}
while(p!=xk);
if(l[p]!=65535)
{cout<<"Put: "<<path[p+1]<<endl;
cout<<"Dlina puti: "<<l[p]<<endl;}
else
cout<<"takogo puti ne syshestvuet!"<<endl;
getch();}
