Тема: Минимизация ПФ и не полностью определённых ПФ.
Задание №1
Пусть дана функция от трех переменных f(x, y, z)=(0,1,1,1,1,1.1,0). Найти её МДНФ методом неопределённых коэффициентов.
Решение:
Построим таблицу истинности для данной функции. Она будет иметь следующий вид:
| x | y | z | f(x,y,z) | |
| В ДНФ общего вида такой функции будет | ||||
| 26 неопределенных коэффициентов. Для обо‑ | ||||
| значения этих коэффициентов будем | ||||
| использовать букву К с нижним индексом, | ||||
| указывающим конъюнкцию, перед которой | ||||
| стоит этот коэффициент. С учетом всех | ||||
| принятых обозначений ДНФ общего вида | ||||
| запишется так: |
1. ДНФ = k 
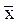 Ú kx x Ú k
Ú kx x Ú k 
 Ú ky y Ú k
Ú ky y Ú k 
 Ú kz z Ú k
Ú kz z Ú k 

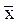
 Ú k
Ú k  y
y 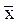 y
y
Ú kx  x
x  Ú kx y x y Ú k
Ú kx y x y Ú k 

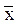
 Ú k
Ú k  z
z 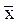 z Ú kx
z Ú kx  x
x  Ú kx z x z
Ú kx z x z
Ú k 


 Ú k
Ú k  z
z  z Ú ky
z Ú ky  y
y  Ú ky z y z Ú k
Ú ky z y z Ú k 


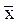

 Ú k
Ú k 
 z
z 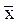
 z
z
Ú k  y
y 
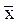 y
y  Ú k
Ú k  y z
y z 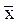 y z Ú kx
y z Ú kx 
 x
x 
 Ú kx
Ú kx  z x
z x  z Ú kx y
z Ú kx y  x y
x y 
Ú kx y z x y z
2. Теперь последовательно подставляя в ДНФ каждый набор значений переменных и приравнивая при этом получаемые выражения к значению функции на этом наборе, получим следующую систему уравнений:
ДНФ(0,0,0): k  Ú k
Ú k  Ú k
Ú k  Ú k
Ú k 
 Ú k
Ú k 
 Ú k
Ú k 
 Ú k
Ú k 

 =0;
=0;
ДНФ(0,0,1): k  Ú k
Ú k  Ú kz Ú k
Ú kz Ú k 
 Ú k
Ú k  z Ú k
z Ú k  z Ú k
z Ú k 
 z =1;
z =1;
ДНФ(0,1,0): k  Ú ky Ú k
Ú ky Ú k  Ú k
Ú k  y Ú k
y Ú k 
 Ú ky
Ú ky  Ú k
Ú k  y
y  =1;
=1;
ДНФ(0,1,1): k  Ú ky Ú kz Ú k
Ú ky Ú kz Ú k  y Ú k
y Ú k  z Ú ky z Ú k
z Ú ky z Ú k  y z =1;
y z =1;
ДНФ(1,0,0): kx Ú k  Ú k
Ú k  Ú kx
Ú kx  Ú kx
Ú kx  Ú k
Ú k 
 Ú kx
Ú kx 
 =1;
=1;
ДНФ(1,0,1): kx Ú k  Ú kz Ú kx
Ú kz Ú kx  Ú kx z Ú k
Ú kx z Ú k  z Ú kx
z Ú kx  z =1;
z =1;
ДНФ(1,1,0): kx Ú ky Ú k  Ú kx y Ú kx
Ú kx y Ú kx  Ú ky
Ú ky  Ú kx y
Ú kx y  =1;
=1;
ДНФ(1,1,1): kx Ú ky Ú kz Ú kx y Ú kx z Ú ky z Ú kx y z =0;
3. Выполним шаг 3, приравнивая все коэффициенты первого и последнего уравнений к нулю.
4. Вычеркнув все нулевые коэффициенты, получим новую систему уравнений, в которой число неизвестных меньше, чем в исходной, но все же превышает число самих уравнений: k  z Ú k
z Ú k  z Ú k
z Ú k 
 z =1;
z =1;
k  y Ú ky
y Ú ky  Ú k
Ú k  y
y  =1;
=1;
k  y Ú k
y Ú k  z Ú k
z Ú k  y z =1;
y z =1;
kx  Ú kx
Ú kx  Ú kx
Ú kx 
 =1;
=1;
kx  Ú k
Ú k  z Ú kx
z Ú kx  z =1;
z =1;
kx  Ú ky
Ú ky  Ú kx y
Ú kx y  =1;
=1;
В каждом уравнении полученной системы имеется по два коэффициента, которые могут быть приравнены к 1. Отсюда вытекает неоднозначность решения задачи. Учитывая то, что в каждом уравнении следует выбрать лишь один коэффициент, получим следующие два решения:
Первое: k  z =1; ky
z =1; ky  =1; kx
=1; kx  =1;
=1;
Второе: k  z =1; k
z =1; k  y =1; kx
y =1; kx  =1;
=1;
Остальные коэффициенты в обоих случаях приравниваем к нулю.
5. Подставляя найденные коэффициенты в исходную ДНФ, получим две минимальных ДНФ для заданной функции:
МДНФ1 = 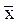 z Ú y
z Ú y  Ú x
Ú x  ; и
; и
МДНФ2 =  z Ú
z Ú 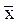 y Ú x
y Ú x  ;
;
Задание№2
Пусть функция от трех переменных f(x, y, z) задана в виде f(x,y,z)=(1,0,0,0,1,0,1,1). Построить её СокрДНФ.
Решение:
Для нахождения СокрДНФ необходимо построить СДНФ. Для данной функции СДНФ будет иметь вид: f(x, y, z) = 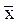

 Ú x
Ú x 
 Ú x y
Ú x y  Ú x y z
Ú x y z
Используя законы склеивания ( x A Ú 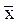 B = x A Ú
B = x A Ú 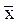 B Ú AB - склеивание; или x A Ú
B Ú AB - склеивание; или x A Ú 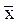 A = A - полное склеивание или x A Ú
A = A - полное склеивание или x A Ú 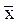 A = x A Ú
A = x A Ú 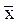 A Ú A - неполное склеивание)
A Ú A - неполное склеивание)
выполним всевозможные склеивания, т.е. будем склеивать первую конъюнкцию со второй, третьей, четвертой, затем вторую с третьей и четвертой, и наконец, третью с четвертой.
Тогда f(x, y, z) = 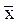

 Ú x
Ú x 
 Ú x y
Ú x y  Ú x y z Ú
Ú x y z Ú 
 Ú
Ú 
 y
y 
Ú 
 y z Ú x
y z Ú x  Ú x
Ú x  x z Ú x y =
x z Ú x y = 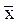

 Ú x
Ú x 
 Ú x y
Ú x y  Ú x y z
Ú x y z
Ú 
 Ú x
Ú x  Ú x y
Ú x y
Теперь выполняя всевозможные поглощения (A Ú AB = A - поглощение, где A и B - элементарные конъюнкции), получим:
f(x, y, z) = 
 Ú x
Ú x  Ú x y
Ú x y
Поскольку преобразования больше невозможны, последняя формула является СокрДНФ.
Задания для самостоятельного решения:
Задание №1
Пусть дана функция от трех переменных f(x, y, z). Найти её МДНФ методом неопределённых коэффициентов.
Задание№2
Пусть дана функция от четырёх переменных f(x, y, z, w). Построить её СокрДНФ.
Варианты заданий:
Вариант №1
1. f(x,y,z)=(2,3,5,6)
2. f(x,y,z)=(3,6,7,8,10,11,14)
Вариант №2
1. f(x,y,z)=(1,2,3,7)
2. f(x,y,z)=(2,3,4,5,10,12,13,15)
Вариант №3
1. f(x,y,z)=(0,3,4,5)
2. f(x,y,z)=(6,7,8,10,11,13)
Вариант №4
1. f(x,y,z)=(5,6,7)
2. f(x,y,z)=(2,4,6,9,10,11,12,13)
Вариант №5
1. f(x,y,z)=(1,2,4,5,6,7)
2. f(x,y,z)=(2,4,5,6,8,11,12,14)
Вариант №6
1. f(x,y,z)=(0,2,3,5,7)
2. f(x,y,z)=(2,3,5,6,7,8,10,12,14)
Вариант №7
1. f(x,y,z)=(0,3,5,7)
2. f(x,y,z)=(2,3,4,5,12,13,14)
Вариант №8
1. f(x,y,z)=(0,1,2,3)
2. f(x,y,z)=(1,2,5,7,8,12,13,14)
Вариант №9
1. f(x,y,z)=(1,2,4,6,7)
2. f(x,y,z)=(1,5,6,7,8,9,10,15)
Вариант №10
1. f(x,y,z)=(0,1,2,3,4)
2. f(x,y,z)=(2,3,9,10,13,14,15)
Вариант №11
1. f(x,y,z)=(1,3,4,6)
2. f(x,y,z)=(0,2,5,6,8,11,12,13)
Вариант №12
1. f(x,y,z)=(2,4,5,7)
2. f(x,y,z)=(1,4,6,7,10,11,12,14)
Вариант №13
1. f(x,y,z)=(1,2,3,6)
2. f(x,y,z)=(0,2,5,7,8,9,11,12)
Вариант №14
1. f(x,y,z)=(0,1,2,3,4)
2. f(x,y,z)=(1,2,5,7,8,9,10,11,15)
Вариант №15
1. f(x,y,z)=(0,1,2,6)
2. f(x,y,z)=(3,5,6,7,8,9,13,14)
Вариант №16
1. f(x,y,z)=(2,3,6,7)
2. f(x,y,z)=(0,1,2,7,8,9,10,13,14)
Вариант №17
1. f(x,y,z)=(3,4,5,6)
2. f(x,y,z)=(2,6,7,10,12,14,15)
Вариант №18
1. f(x,y,z)=(3,4,6,7)
2. f(x,y,z)=(1,2,4,5,8,9,11,12)
Вариант №19
1. f(x,y,z)=(3,5,6,7)
2. f(x,y,z)=(3,4,5,6,8,9,10,11)
Вариант №20
1. f(x,y,z)=(0,5,6,7)
2. f(x,y,z)=(1,3,5,8,9,10,11,12)
Практическая работа №8
