Типові ланки САК і їхні характеристики

Пропорційна ланка. Інтегруюча ланка. Диференцююча ланка. Аперіодична ланка першого порядку. Форсуюча ланка. Коливальна ланка. Ланка запізнення.

Функціональні елементи, використовувані в автоматичних системах, можуть мати всіляке конструктивне виконання і всілякі принципи дії. Однак спільність математичних виразів, що зв'язують вхідні та вихідні величини цих елементів, дозволяє виділити обмежене число так званих типових алгоритмічних ланок, під якими розуміють штучно виділену частину САК, що відповідає деякому елементарному математичному алгоритму.

На практиці найчастіше зустрічають наступні шість типових ланок:

- пропорційна;

- інтегруюча;

- диференцююча;

- аперіодична 1-го порядку;

- форсуюча;

- коливальна.

Крім цього до основних типових ланок відносять також особливу ланку - запізнення.

Знання властивостей перерахованих ланок істотно полегшує аналіз САК, тому що будь-який елемент системи і уся система в цілому можуть бути представлені у вигляді однієї або з'єднання декількох типових ланок. При цьому вивчають:

- рівняння ланки;

- передатну функцію;

- частотні характеристики - АФЧХ, ЛАЧХ, ЛФЧХ ;

- часові характеристики - і .

У табл. 4.1 наведені властивості типових ланок

Таблиця 4.1 – Властивості типових ланок

Назва ланки	Рівняння ланки	Графіки характеристик
Пропорційна
Інтегруюча
Диференцююча
Аперіодична першого порядку
Форсуюча
Коливальна
Запізнення

Контрольні запитання

1. Як буде змінюватися вихідний сигнал безінерційної ланки, якщо на її вхід подати лінійний вплив? Побудуйте графік.

2. Як впливає безінерційна ланка на амплітуду і фазу синусоїдального вхідного сигналу?

3. Запишіть передатну функцію інерційної ланки першого порядку.

4. Як проходять через інерційну ланку першого порядку гармонійні сигнали низької і високої частоти?

5. При якому значенні коефіцієнта демпфірування інерційна ланка другого порядку має аперіодичний перехідний процес а при якому - коливальний?

6. У чому подібність і відмінність частотних властивостей інтегруючих та інерційних статичних ланок?

7. Чому диференцюючі ланки погано пропускають повільно мінливі вхідні сигнали?

8. Побудуйте графік вихідного сигналу ланки запізнювання при подачі на її вхід лінійного впливу.

9. Напишіть передатну функцію ланки запізнювання.

10. Назвіть параметри коливальної ланки, що характеризують її динамічні властивості.

Стійкість САК

Поняття, види та загальна умова стійкості. Алгебраїчні критерії стійкості. Частотні критерії стійкості. Критерій Михайлова. Критерій Найквіста. Визначення стійкості за логарифмічними частотними характеристиками. Порівняльна оцінка критеріїв стійкості. Запаси стійкості. Вплив величини передатного коефіцієнта розімкнутого контуру САК на її стійкість у замкнутому стані.

Однією з найважливіших характеристик автоматичної системи керування є стійкість. Цим поняттям характеризують працездатність системи.

Стійкість автоматичної системи - це властивість системи повертатися у вихідний стан рівноваги після припинення дії збурення, яке вивело систему із цього стану.

Система є стійкою, якщо вільна складова перехідного процесу із часом прагне до нуля, тобто якщо

. (5.1)

Для стійкості лінійної САК необхідно і достатньо, щоб дійсні частини всих коренів характеристичного рівняння системи були негативними (див. рис. 5.1).

Рис. 5.1 - Вплив коренів характеристичного рівняння системи на складові її вільного руху

У ТАК розроблено ряд правил, за допомогою яких можна судити про знаки коренів, не вирішуючи характеристичне рівняння і не знаходячи числові значення самих коренів. Ці правила називаються критеріями стійкості.

Найпростішим критерієм стійкості є умова позитивності коефіцієнтів характеристичного рівняння. Позитивність коефіцієнтів рівняння є необхідною (але не достатньою) умовою стійкості системи. Це означає, що якщо усі коефіцієнти позитивні, то система може бути стійкою або нестійкою. Але якщо хоча б один коефіцієнт рівняння негативний або дорівнює нулю, то система нестійка.

Критерії стійкості можуть бути алгебраїчними і частотними.

Алгебраїчні критерії встановлюють необхідні та достатні умови від’ємності коренів у формі обмежень, що накладаються на певні комбінації коефіцієнтів характеристичного рівняння.

Частотні критерії визначають зв'язок між стійкістю системи і формою частотних характеристик системи.

Досить розповсюдженим в інженерній практиці є критерій Гурвіца.

Стосовно до завдань теорії керування критерій Гурвіца можна сформулювати так: система, описана характеристичним рівнянням

. (5.2)

стійка, якщо при позитивні всі визначники Гурвіца .

Ці визначники складаються за наступними правилами:

1) за головною діагональю виписують всі коефіцієнти від до в порядку зростання індексу;

2) доповнюють стовпці визначника нагору від діагоналі коефіцієнтами з послідовно зростаючими, а вниз – з послідовно зменшуючимися індексами;

3) на місце коефіцієнтів, індекси яких більше n і менше 0, ставлять нулі.

Відповідно до цих правил, визначник Гурвіца -го порядку для рівняння (3.1) має вигляд

(5.3)

Частотні критерії стійкості дозволяють судити про стійкість САК по виду її частотних характеристик. Ці критерії є графоаналітичними і мають широке поширення, тому що дозволяють порівняно легко досліджувати стійкість систем високих порядків, а також мають просту геометричну інтерпретацію. До цієї групи належать критерії Михайлова і Найквіста.

Критерій стійкості Михайлова можна сформулювати так: для того, щоб САК була стійка, необхідно і достатньо, щоб годограф Михайлова при зміні частоти від 0 до , починався при на речовинній позитивній півосі і обходив проти годинникової стрілки послідовно квадрантів координатної площини, де - порядок характеристичного рівняння, не звертаючись при цьому у нуль.

Годографи кривої Михайлова при зміні від 0 до ¥ для стійких систем при різних значеннях наведені на рис. 5.2.

Рис. 5.2

Критерій Найквіста дозволяє судити про стійкість замкнутої системи по АФЧХ її розімкнутого контуру.

Замкнута система буде стійка, якщо АФЧХ розімкнутої системи, що має правих коренів, при збільшенні від 0 до охопить точку [ ; ] раз у позитивному напрямку.

Критерій Найквіста дозволяє з'ясувати стійкість замкнутої системи не тільки по АФЧХ, але й по ЛФЧХ розімкнутої системи. Цю можливість використовують досить широко через простоту побудови таких характеристик.

Якщо розімкнута система стійка, то для забезпечення її стійкості в замкнутому стані необхідно і достатньо, щоб при досягненні ФЧХ розімкнутої системи значення , ЛАЧХ цієї ж системи була негативною.

Визначення факту стійкості за рівняннями першого наближення не дає повної впевненості в тому, що практично створена система буде стійка при всіх можливих значеннях параметрів. Тому в ТАК роблять так само, як у будь-який іншій інженерній дисципліні - виконують розрахунки за наближеними рівняннями з урахуванням поправочних коефіцієнтів (запасів стійкості).

Запасом стійкості за модулем при АФЧХ називають мінімальний відрізок дійсної осі , яка характеризує відстань між критичною точкою і найближчою точкою перетинання годографа з дійсною віссю (рис. 5.3,а).

У випадку клювоподібної АФЧХ запас стійкості за модулем визначається величинами двох відрізків дійсної осі - і між критичною точкою [ ; ] і АФЧХ (Рис. 5.3,б).

Запасом стійкості по фазі називають мінімальний кут , утворений радіусом, що проходить через точку перетинання годографа з окруж- ністю одиничного радіуса із центром на початку координат і негативною частиною дійсної осі.

Рис. 5.3

У більшості систем зростання передатного коефіцієнта вище його критичного значення приводить до порушення стійкості, а його зменшення нижче критичного значення - до стабілізації системи. У системах із клюво- подібними характеристиками при збільшенні передатного коефіцієнта вище його критичного значення система може перетворитися з нестійкої в стійку, а при зменшенні - з стійкої в нестійку.

Значення , у свою чергу, визначається іншими параметрами системи.

Граничне значення передатного коефіцієнта розімкнутого контуру системи залежить від співвідношення постійних часу окремих ланок і не залежить від їхніх абсолютних значень.

Приклад 5.1.

САК описується рівнянням другого порядку, характеристичне рівняння якого має вигляд: . Визначити умови стійкості САК по Гурвіцу.

Вирішення.

Складемо відповідно до (5.10) головний визначник Гурвіца:

,

Тоді умови стійкості системи запишемо у вигляді

; ; .

Оскільки , то для виконання умови , коефіцієнт також повинен бути більше нуля. Таким чином, для стійкості системи другого порядку необхідно і достатньо, щоб всі коефіцієнти характеристичного рівняння були позитивними.

Приклад 5.2.

Перевірити стійкість САК за допомогою критерію Найквіста при наступних параметрах об'єкта керування і І-регулятора: , , , .

Вирішення.

Запишемо частотну функцію розімкнутого контуру системи в алгебраїчному вигляді

Отримана залежність дозволяє побудувати годограф (рис. 5.4).

Рис. 5.4

Як видно з рисунка годограф не охоплює точку [ ; ], перетинаючи вісь абсцис у точці [0,58; ], що свідчить про достатні запаси стійкості: і .

Контрольні запитання

1. Поясніть поняття "стійкість САК".

2. Що значить "стійкість у малому" і "стійкість у великому"?

3. Чому при дослідженні стійкості САК досить знати тільки однорідне диференційне рівняння?

4. У чому полягають недоліки аналізу стійкості по коренях характеристичного рівняння?

5. Перелічіть критерії стійкості і вкажіть їхні особливості.

6. Що таке годограф Михайлова?

7. Що таке граничний передатний коефіцієнт?

8. Як зв'язане розташування коренів характеристичного рівняння зі стійкістю системи?

Якість САК

Точність роботи САК в сталих режимах. Метод коефіцієнтів помилок. Точність роботи САК в перехідних режимах.

Крім забезпечення вимоги стійкості САК повинна мати певну якість, під якою розуміється точність процесу керування. Кількісною оцінкою точності служить величина помилки , обумовлена різницею між заданим і фактичним значеннями керованої величини:

. (6.1)

При цьому розрізняють дві функції САК:

- відтворення задаючого впливу;

- придушення (компенсація) збурювань.

Через інерційність системи обидві перераховані функції завжди виконуються з деякою погрішністю, тобто звичайно .

Величина помилки визначається як властивостями системи, так і виглядом вхідних впливів. Для оцінки сталих режимів САК використовують наступні типові закони зміни вхідних впливів:

- незмінність задаючого і збурюючого впливів, тобто і ;

- рух системи з постійною швидкістю, тобто й ;

- рух системи з постійним прискоренням, тобто і ;

- рух системи за гармонійним законом, тобто і .

Аналіз точності роботи САК у складних сталих режимах зручно робити на основі т.зв. методу коефіцієнтів помилок. Цей метод ґрунтується на наближеній заміні передатної функції помилки, викликаної вхідним впливом 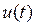на околицях точки , що в області оригіналів відповідає , рядом Маклорена (при ватного випадку ряду Тейлора при ).

Точність роботи у перехідних режимах визначається сукупністю окремих миттєвих значень помилки . З метою стандартизації показників якості у цьому випадку прийнято використовувати перехідні характеристики за каналом завдання і каналом збурювання при подачі на відповідні входи типових сигналів вигляду 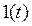, які в узагальненому вигляді характеризують значення .

Показники якості, залежно від способу їхнього визначення, розділяють на прямі і непрямі.

При загальній оцінці якості, насамперед, звертають увагу на форму перехідного процесу. Розрізняють наступні типи перехідних процесів (див. рис. 6.1): коливальні (1); аперіодичні (2); монотонні (3).

а) б)

Рис. 6.1:

а) перехідні характеристики;

б) імпульсні перехідні характеристики

Найбільша кількість прямих показників введена для характеристики якості коливального процесу по каналу завдання. (див. рис. 6.2).

Рис. 6.2

До основних показників характеристики відносяться перерегулювання та час регулювання .

Перерегулювання визначають максимальним відхиленням керованої величини від її сталого значення , вираженим в % до :

. (6.2)

Час регулювання – час, після закінчення якого відхилення характеристики від сталого значення стає і залишається менше зони нечутливості системи . Цей показник характеризує швидкість протікання перехідного процесу.

Непрямі показники якості визначаються без побудови перехідних процесів і підрозділяються на кілька груп:

- кореневі показники;

- частотні показники;

- інтегральні показники.

Основний вплив на тривалість перехідних процесів роблять корені, розташовані ближче інших до мнимої осі, тому що вони дають найбільш повільно загасаючі складові. Дійсна частина такого кореня називається ступенем стійкості .

Основний вплив на коливальні властивості перехідних процесів робить пара комплексно сполучених коренів, для яких відношення є найбільшим. Величину називають коливальністю САК.

Про якість САК можна судити, скориставшись дійсною частиною функції . Справа в тому, що у випадку одиничного східчастого впливу і нульових початкових умов між перехідною характеристикою та частотною передатною функцією системи існує однозначний зв'язок за допомогою перетворення Фур'є:

, (6.3)

Використовують наступні частотні показники якості.

Показник коливальності - відношення максимального значення АЧХ системи до значення цієї АЧХ при , тобто

. (6.4)

Показник коливальності характеризує схильність системи до коливань.

Резонансна частота - частота, при якій АЧХ системи має екстремум. Гармонійні коливання, що мають частоту , проходять через САК з найбільшим посиленням.

Смуга пропущення - діапазон частот гармонійних коливань, “пропуску” системою, тобто тих, що проходять через систему із практично помітними коливаннями вихідної змінної.

Частота зрізу - частота, при якій АЧХ із ростом частоти зменшуючись, переходить від значень, більших одиниці, до значень, менших одиниці, і залишається в цьому діапазоні при подальшому збільшенні частоти.

У самому загальному вигляді всі інтегральні показники можна представити інтегралом:

, (6.5)

де - деяка функція системи, що характеризує її стан.

При оцінці якості системи по каналу завдання найпростішим інтегральним показником є лінійна інтегральна оцінка, що використовує перехідну характеристику :

(6.6)

яка дорівнює площі між прямою і кривою перехідного процесу .

На практиці найчастіше застосовують квадратичний інтегральний критерій вигляду:

. (6.7)

Цей критерій не залежить від знака і, отже, може бути застосований як для монотонних, так і для коливальних процесів.

Відмітимо, що мінімізація інтегральної квадратичної помилки (6.7) приводить до великих перерегулювань перехідного процесу (до 20 % від сталого значення ). У зв'язку із цим застосовують інтегральні критерії, що враховують не тільки величину помилки, але і швидкість її зміни:

, (6.8)

де – ваговий коефіцієнт, що визначає значимість другого елементу підінтегральної функції.

Іноді крім зазначених обмежень враховують і обмеження на прискорення. Тоді інтегральний критерій приймає вигляд:

. (6.9)

Підкреслимо, що всі розглянуті інтегральні оцінки є функцією параметрів системи, отже, їх можна мінімізувати, змінюючи параметри системи і, насамперед, пристрою керування.

Контрольні запитання

1. Які властивості автоматичної системи прийнято розглядати при оцінці її якості?

2. Які ви знаєте прямі показники якості?

3. Що таке перерегулювання? Яку роль грає цей показник?

4. Як визначається величина часу регулювання?

5. Що таке частота зрізу? Що ця частота показує?

6. Як впливає передатний коефіцієнт розімкнутого контуру на статичну і динамічну точність систем?

7.Укажіть характерні ознаки передатних функцій у статичній системі регулювання.

8. Яка система називається астатичною? Від наявності яких типових ланок у контурі системи залежить її астатизм?

9. По якій динамічній характеристиці системи регулювання оцінюють прямі показники якості? Які з них характеризують коливальність системи, а які - її швидкодію?

10. Як зв'язане розташування коренів характеристичного рівняння з коливальністю системи?

11. Як зв'язаний найближчий дійсний корінь характеристичного рівняння із тривалістю перехідного процесу?

12. Як впливають параметри розімкнутого контуру на динамічні властивості замкнутої системи?

13. Які параметри графіка перехідного процесу враховуються інтегральними оцінками?

14. Який із двох перехідних процесів краще - з великою інтегральною оцінкою або малою? Чому?

15. Для яких перехідних процесів можна застосовувати лінійну інтегральну оцінку?

16. Чому для коливальних перехідних процесів доводиться застосовувати модульні або квадратичні оцінки?

Індивідуальне завдання

Програмою курсу передбачене виконання індивідуального завдання. До виконання цього завдання варто приступати тільки після вивчення всіх розділів курсу і відповідей на контрольні запитання.

Розрахунки повинні супроводжуватися короткими, вичерпними поясненнями. Креслення та схеми варто виконувати ретельно із вказівкою відповідних підписів.

Вихідні дані

Задано принципову схему системи стабілізації швидкості обертання електродвигуна постійного струму незалежного збудження (див. рис.1.7). Чисельні значення параметрів елементів схеми наведені в табл. 7.1.

Завдання

1.Дати короткий опис роботи САК за принциповою схемою.

2. Скласти функціональну схему САК.

3. Скласти диференціальні рівняння окремих елементів САК і визначити їхні передатні функції.

4. Скласти структурну схему САК.

5. Визначити передатні функції замкнутої САК.

6. Визначити граничне значення передатного коефіцієнта напівпровідникового підсилювача , при якому САК ще стійка.

7. Визначити перехідну характеристику системи по каналу задаючого впливу при , обраному усередині діапазону стійкості.

Таблиця 7.1 - Вихідні дані індивідуального завдання

№ завдання	Параметри генератора	Параметри електродвигуна	,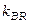
,	,	,	,	,	,
		26,6		0,03	0,29	1,3	0,6	0,00025
				0,02	0,093	1,1	0,8	0,0003
				0,025	0,14	3,5	0,9	0,0001
				0,028	0,224	3,2	0,7	0,0002
		26,6		0,03	0,29	1,3	0,6	0,00015
				0,018	0,093		0,7	0,0002
				0,02	0,14	3,5	0,8	0,00025
				0,03	0,224	3,2	0,9	0,0003
		26,6		0,03	0,29	1,3	0,6	0,00035
				0,018	0,093		0,8	0,00015
				0,022	0,14	3,5	0,9	0,0002
				0,03	0,224		0,7	0,00025
		26,6		0,03	0,29	1,3	0,6	0,0003
				0,016	0,093		0,7	0,00035
				0,02	0,14	3,5	0,8	0,0004
				0,023	0,224		0,9	0,00015
		26,6		0,032	0,29	1,3	0,6	0,0002
				0,012	0,093	1,1	0,8	0,00025
				0,02	0,14	3,5	0,9	0,0003
				0,03	0,224		0,7	0,00035
		26,6		0,03	0,29	1,3	0,6	0,0004
				0,012	0,093		0,7	0,00015
				0,016	0,14	3,5	0,8	0,0002
				0,018	0,224		0,9	0,00025
		26,6		0,028	0,29	1,3	0,6	0,0003
				0,028	0,224	1,3	0,6	0,0003
		26,6		0,03	0,29		0,7	0,00035
				0,018	0,093	3,5	0,8	0,0004
				0,02	0,14	3,2	0,9	0,00015
				0,03	0,224	1,3	0,6	0,0002
		26,6		0,03	0,29		0,8	0,00025
				0,018	0,093	3,5	0,9	0,0003
				0,022	0,14	3,5	0,7	0,00035
				0,03	0,224		0,6	0,0004
		26,6		0,03	0,29	1,3	0,7	0,00015

Закінчення таблиці 7.1

№ завдання	Параметри генератора	Параметри електродвигуна	,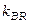
,	,	,	,	,	,
				0,016	0,29	1,1	0,8	0,0002
				0,012	0,093	3,5	0,6	0,00025
	26,6			0,02	0,14		0,8	0,00025
				0,03	0,224	1,3	0,9	0,0003
				0,03	0,29		0,7	0,00035
				0,012	0,093	3,5	0,6	0,00015
	26,6			0,016	0,14		0,7	0,0002
				0,018	0,224	1,3	0,8	0,00025
				0,028	0,29	1,3	0,9	0,0003
				0,02	0,093		0,6	0,00035
	26,6			0,025	0,14	3,2	0,8	0,0004
				0,028	0,224	1,3	0,9	0,00015
				0,03	0,29		0,7	0,0002
				0,018	0,093	3,5	0,6	0,00025
				0,02	0,093	3,2	0,7	0,0003