Общее решение уравнений классической электродинамики

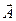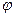Уравнения классической электродинамики для потенциалов электромагнитного поля с учётом калибровки Лоренца имеют вид неоднородных уравнений Даламбера. Допустим, что и - решения этих уравнений, а векторы 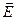и 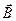определены "стандартным" способом:

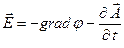
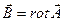
Дополнительно рассмотрим однородную систему уравнений классической электродинамики ( 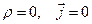) и введём потенциалы электромагнитного поля 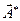и 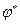следующим образом:

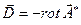
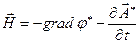
это можно сделать, поскольку для однородной системы уравнений Максвелла .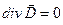

При этом имеют место зависимости

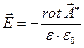
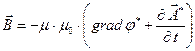
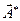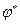а и - решения однородных уравнений Даламбера, общее решение для силовых составляющих электромагнитного поля можно записать как

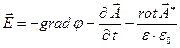
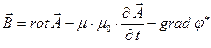
Проводящая однородная изотропная среда в отсутствие сторонних электрических зарядов.

Система уравнений Максвелла для рассматриваемого случая

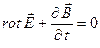
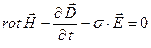
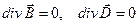
Поскольку дивергенция поля магнитной индукции и дивергенция поля вектора электрического смещения обе равны нулю, потенциалы электромагнитного поля можно ввести либо классическим способом ( ), либо альтернативным, как это было сделано в предыдущем случае. В классическом варианте уравнения для потенциалов электромагнитного поля имеют вид

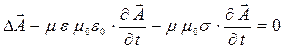
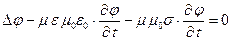
Если в качестве дополнительного условия положить

,

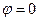получим следующие соотношения:

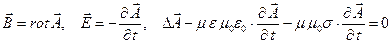
Если исходить из условия 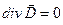, получим:

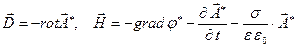
С учётом калибровки Лоренца

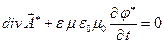
получаем:

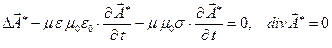
Из изложенного следует, что потенциалы электромагнитного поля можно вводить различными способами. Множество этих способов не исчерпывается приведёнными примерами. В частности, для однородной изотропной непроводящей среды в отсутствие сторонних электрических зарядов (система уравнений Максвелла - однородная), широкое применение находят потенциалы Герца.

Потенциалы Герца.

Различают потенциал Герца электрического типа и потенциал Герца магнитного типа. Основная идея их введения состоит в попытке свести систему уравнений классической электродинамики для потенциалов электромагнитного поля 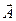и 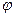к уравнению относительно одной векторной функции. Если окажется, что это уравнение имеет стандартную форму, изученную в математической физике, будем считать, что цель достигнута.

Потенциал Герца электрического типа.

По определению:

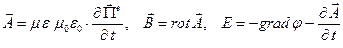
Рассмотрим уравнение

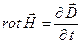
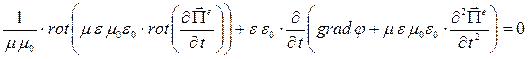
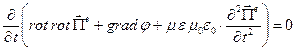
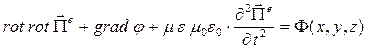
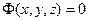
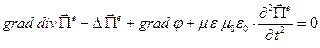
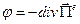
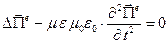
Уравнение для потенциала Герца электрического типа получено, это однородное уравнение Даламбера, методы его решения хорошо известны. В частности, выше с решениями в форме бегущих волн произвольной формы и бегущих плоских гармонических волн мы уже встречались.