Источники электрической энергии

Основные положения и соотношения

Реальный источник электрической энергии можно изобразить двояко: а) в виде генератора напряжения, который характеризуется э.д.с. Е, численно равной напряжению холостого хода источника, и включенной последовательно с сопротивлением r₀ (рис. 1, а), б) в виде генератора тока, который характеризуется током I_к, численно равным току короткого замыкания реального источника, и параллельно соединенной проводимостью g₀ (рис. 1, б).

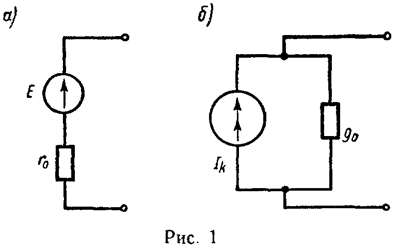
Переход от генератора напряжения к эквивалентному генератору тока осуществляется по формулам

Iк=Er0,    g0=1r0,Iк=Er0,    g0=1r0, (1)

а обратный переход от генератора тока к эквивалентному генератору напряжения по следующим формулам

E=Iкg0,    r0=1g0.E=Iкg0,    r0=1g0. (2)

У идеального генератора напряжения внутреннее сопротивление равно нулю, тогда как у идеального генератора тока внутренняя проводимость равна нулю.

2. Закон Ома

Закон Ома применяется для ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений).

Для написания закона Ома следует прежде всего выбрать произвольно некоторое положительное направление для тока.

а) Для ветви, состоящей только из сопротивлений и не содержащей э.д.с. (например, для ветви mn на рис. 2), при положительном направлении для тока от точки m к точке n ток равен

I=φm−φnrmn=Umnrmn.I=φm−φnrmn=Umnrmn. (3)

Здесь φ_m и φ_n – потенциалы точек m и n, U_mn = φ_m – φ_n – разность потенциалов или напряжение между точками m и n, r_mn = r₄ + r₅ – полное сопротивление ветви между точками m и n.

Пример – в задаче 17.

б) Для замкнутой одноконтурной цепи

I=ΣEΣr,I=ΣEΣr, (4)

где Σr – арифметическая сумма всех внешних и внутренних сопротивлений цепи, ΣE – алгебраическая сумма ее электродвижущих сил.

Со знаком плюс берут те э.д.с., направления которых совпадают с выбранным положительным направлением для тока, и со знаком минус – э.д.с. с противоположными направлениями.

Примеры – в задачах 15 и 17.

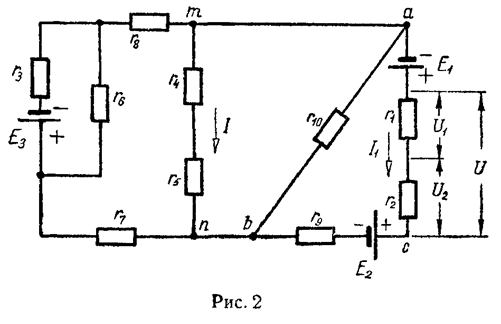
в) Для ветви, содержащей э.д.с. и сопротивления (например, для ветви acb на рис. 2),

I1=φa−φb+ΣEΣrab=Uab+E1−E2r1+r2+r9,I1=φa−φb+ΣEΣrab=Uab+E1−E2r1+r2+r9, (5)

где U_ab = φ_a – φ_b – напряжение на концах ветви acb, отсчитываемое по выбранному положительному направлению тока, ΣE – алгебраическая сумма э.д.с., находящихся в этой ветви, а Σr – арифметическая сумма ее сопротивлений.

Формулу (5) называют обобщенным законом Ома.

Примеры – в задачах 15 и 17.

3. Законы Кирхгофа

Для написания законов Кирхгофа следует прежде всего задаться положительными направлениями для токов в каждой ветви.

Первый закон Кирхгофа

∑k=1nIk=0,∑k=1nIk=0, (6)

Алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. Токи, притекающие к узлу, условно принимаются положительными, а вытекающие из него – отрицательными (или наоборот).

Второй закон Кирхгофа

∑k=1nIk⋅rk=∑k=1nEk.∑k=1nIk⋅rk=∑k=1nEk. (7)

Алгебраическая сумма падений напряжений любого замкнутого контура равна алгебраической сумме э.д.с. в нем.

Направление обхода контура выбирается произвольно. При записи левой части равенства со знаком плюс берутся падения напряжения в тех ветвях, в которых положительное направление тока совпадает с направлением обхода (независимо от направления э.д.с. в этих ветвях), и со знаком минус – падения напряжения в тех ветвях, в которых положительное направление, тока противоположно направлению обхода. При записи правой части равенства э.д.с., направления которых совпадают с выбранным направлением обхода (независимо от направления тока, протекающего через них), принимаются положительными, а э.д.с., направленные против выбранного направления обхода, принимаются отрицательными.

Пример – в задаче 29.

Распределение напряжений при последовательном соединении двух сопротивлений (см. рис. 2)

I1=U1r1=U2r2=Ur1+r2,I1=U1r1=U2r2=Ur1+r2,

U1=U⋅r1r1+r2,   U2=U⋅r2r1+r2.U1=U⋅r1r1+r2,   U2=U⋅r2r1+r2. (8)

Распределение токов в двух параллельных ветвях – формула разброса токов или формула делителя токов (рис. 3)

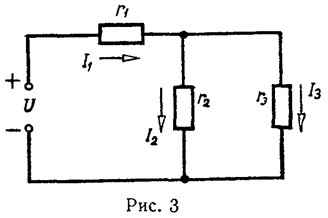
U2=U3=U2,3,    I2⋅r2=I3⋅r3=I1⋅r2,3=I1⋅r2⋅r3r2+r3,U2=U3=U2,3,    I2⋅r2=I3⋅r3=I1⋅r2,3=I1⋅r2⋅r3r2+r3,

I2=I1⋅r3r2+r3,     I3=I1⋅r2r2+r3.I2=I1⋅r3r2+r3,     I3=I1⋅r2r2+r3. (9)

Распределение напряжений при последовательном соединении n сопротивлений

Uk=U⋅rk∑k=1nrk.Uk=U⋅rk∑k=1nrk.

Распределение токов в n параллельных ветвях

Ik=I⋅gk∑k=1ngk.Ik=I⋅gk∑k=1ngk.