Расчет цепи по уравнениям Кирхгофа
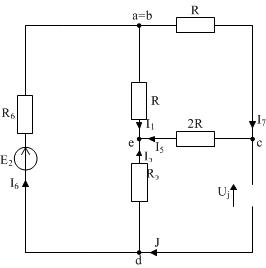
В схеме (рисунок 5) 5 узлов, следовательно, составляется 4 уравнения (в качестве опорного выбран узел e).
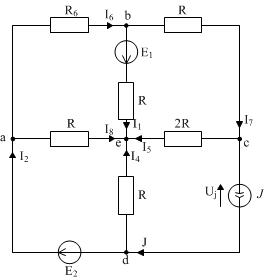 Уравнения по I закону Кирхгофа:
Уравнения по I закону Кирхгофа:
Для узла а:I6+I8 – I2 = 0
Для узла b:–I6 + I1 + I7 = 0
Для узла с:– I7 + I5 = – J
Для узла d:I2 + I4 = J
| Рисунок 5 |
Для того чтобы написать уравнения по II закону Кирхгофа, нужно выбрать положительные направления обхода контуров, пусть таковыми будут направления по часовой стрелке.
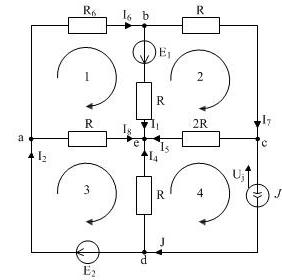 Уравнения по II закону Кирхгофа:
Уравнения по II закону Кирхгофа:
1К:  RI6+RI1 – RI8 = E1
RI6+RI1 – RI8 = E1
2K:RI7 + 2RI5 – RI1 = – E1
3K:RI8 – RI4 = E2
4K:–2RI5 – UJ + RI4 = 0
| Рисунок 6 |
С помощью пакета MathCAD решаем систему уравнений (рисунок 7):
 |
| Рисунок 7 |
Результаты расчета в пакете MathCad:
I1=2.222 A,
I2= 2.848 A,
UJ= –17.935 В,
I4= - 2.248 A,
I5= - 0.526 A,
I6= 2.296 A,
I7= 0.074 A,
I8=0.552 A.
Задание 3
Преобразование схемы до трех контуров
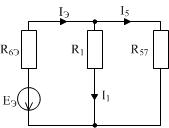
Исходная схема на рисунке 8:

| Рисунок 8 |
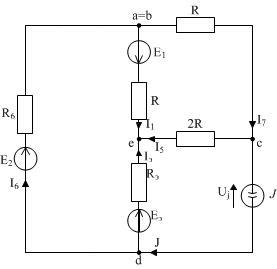 Эквивалентная схема изображена на рисунке 9:
Эквивалентная схема изображена на рисунке 9:
| Рисунок 9 |
Где:
Rэ 
EЭ  E2
E2 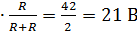
Задание 3.1
Метод контурных токов
Схема с обозначенными контурами изображена на рисунке 10
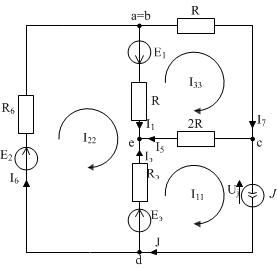
| Рисунок 10 |
Согласно методу контурных токов имеем:
I11 = J
I22 (R6+R+RЭ) – I33R = RЭJ + E2 + E1 – EЭ
– I22R + I33 (R+R+2R) = 2RЭJ – E1
Решаем данную систему в пакете MathCAD (рисунок 11):
A:= 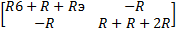 B:= B:= 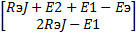 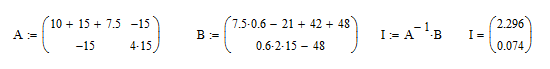 |
| Рисунок 11 |
I11 = 0.6 A
I22 = 2.296 A
I33 = 0.074 A
Токи определяются следующим образом:
I6 = I22 = 2.296 А
I7 = I33 = 0.074 A
I5 = I33 – J = 0.074 – 0.6 = – 0.526 A
I1 = I22 – I33 = 2.296 – 0.074 = 2.222 A
IЭ = - I22 + J = 0.6 – 2.296 = – 1.696 A
Напряжение на источнике тока можно найти по II закону Кирхгофа:
UJ = – EЭ +IЭRЭ – 2RI5 = – 21 – 1.696  7.5 + 2
7.5 + 2  15
15  0.526 = -17.94 В
0.526 = -17.94 В
Таким образом, найденные методом контурных токов токи и напряжение на источнике тока совпадает с результатом расчета методом уравнений Кирхгофа.
Задание 3.2
Метод узловых потенциалов
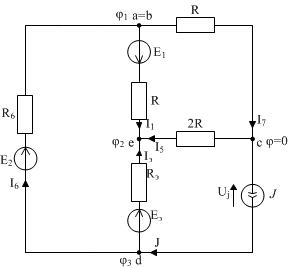 Схема с обозначенными узловыми потенциалами показана на рисунке 12:
Схема с обозначенными узловыми потенциалами показана на рисунке 12:
| Рисунок 12 |
Пусть потенциал узла сравен нулю:
φс = 0
Проводимости:
Y1=Y7=1/R
Y6=1/R6
Y5=1/2R
YЭ=1/RЭ
Уравнения по методу узловых потенциалов:
φ1 (Y7 + Y1 + Y6) – φ2 Y1 - φ3Y6 = -E1Y1 +E2Y6
- φ1 Y1 + φ2 (Y1 + Y5 + YЭ) - φ3 YЭ = E1Y1 + EЭYЭ
- φ1 Y6 - φ2 YЭ + φ3 (YЭ+ Y6) = - EЭYЭ + J – E2Y6
Найденные потенциалы однозначно определяют токи ветвей:
I1= (φ1 - φ2 + E1) Y1
I5= - φ2 Y5
I6= (φ3 – φ1 + E2) Y6
I7= φ1 Y7
IЭ= (φ3 – φ2 + EЭ) YЭ
Воспользуемся пакетом MathCAD для расчетов (рисунок 13):
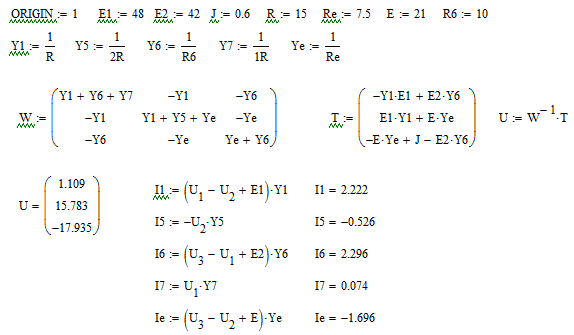 |
| Рисунок 13 |
Результаты:
I1=2.222 A,
I5= - 0.526 A,
I6= 2.296 A,
I7= 0.074 A,
Iэ= - 1.696 A.
Как видно, полученные результаты полностью совпадают с результатами, полученными другими методами ранее.
Задание 3.3
Баланс мощностей
PП=I62R+ I12R+ IЭ2RЭ+ I522R+ I72R =2.2962  15 +2.2222
15 +2.2222  15 +1.6962
15 +1.6962  7.5 + 0.5262
7.5 + 0.5262  30 + 0.0742
30 + 0.0742  15 =156.73 Вт
15 =156.73 Вт
PИ = I6E2 + IЭEЭ + I1E1 + JUJ = 2.296  42 - 1.696
42 - 1.696  21 +2.222
21 +2.222  48 – 0.6
48 – 0.6  17.935
17.935
=156.71 Вт
Допустимая относительная погрешность расчета:
σP=(| PИ – PП |/ PИ)  100% =
100% = 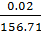
 100% = 0.01%
100% = 0.01%
Задание 3.4
Метод наложения
Искомое напряжение определяется суммой составляющих:
UJ = UJ(E1) + UJ(E2) + UJ(EЭ) + UJ(J)
1.  Оставляем только Е2 как на рисунке 14:
Оставляем только Е2 как на рисунке 14:
| Рисунок 14 |
Имеем схему как на рисунке 15:
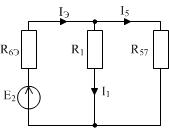
| Рисунок 15 |
UJ(E2) = - I5R5 - IЭRЭ
R57 =R5 + R7=30 + 15 = 45 Ом
R6Э =R6 + RЭ=10 + 7.5 = 17.5 Ом
IЭ= 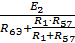 = 42 / 28.75 = 1.461 Ом
= 42 / 28.75 = 1.461 Ом
I5= 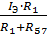 = 21.9 / 60 = 0.365 A
= 21.9 / 60 = 0.365 A
UJ(E2) = - (1.461  7.5 +0.365
7.5 +0.365  30) = – 10.96 – 10.95 =– 21.91 В
30) = – 10.96 – 10.95 =– 21.91 В
2. 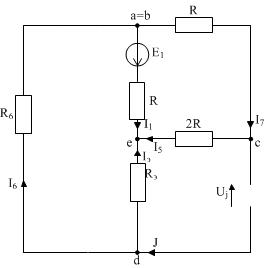 Оставляем только Е1 как на рисунке 16:
Оставляем только Е1 как на рисунке 16:
| Рисунок 16 |
| Рисунок 17 |
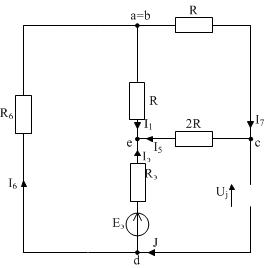
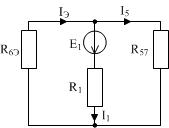 Имеем схему как на рисунке 17:
Имеем схему как на рисунке 17: UJ(E1) = I5R5 - IЭRЭ
R57 =R5 + R7=30 + 15 = 45 Ом
R6Э =R6 + RЭ=10 + 7.5 = 17.5 Ом
I1= 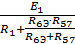 = 48 / 27.5 = 1.739 Ом
= 48 / 27.5 = 1.739 Ом
I5= 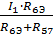 = 30.43 / 62.5 = 0.486 A
= 30.43 / 62.5 = 0.486 A
IЭ= 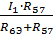 = 78.25 / 62.5 = 1.252 A
= 78.25 / 62.5 = 1.252 A
UJ(E2) = 0.486  30 - 1.252
30 - 1.252  7.5 =14.58 – 9.39 = 5.2 В
7.5 =14.58 – 9.39 = 5.2 В
3.  Оставляем только ЕЭ как на рисунке 18:
Оставляем только ЕЭ как на рисунке 18:
| Рисунок 18 |
| Рисунок 19 |
 Имеем схему как на рисунке 19:
Имеем схему как на рисунке 19: UJ(EЭ) = - I5R5 - IЭRЭ
R57 =R5 + R7=30 + 15 = 45 Ом
R6Э =R6 + RЭ=10 + 7.5 = 17.5 Ом
IЭ= 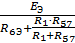 = 21 / 28.75 = 0.73 Ом
= 21 / 28.75 = 0.73 Ом
I5= 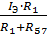 = 10.95 / 60 = 0.1825 A
= 10.95 / 60 = 0.1825 A
UJ(E2) = - (0.1825  30 +0.73
30 +0.73  7.5) = – 5.075 – 5.075 =–10.1 В
7.5) = – 5.075 – 5.075 =–10.1 В
4. 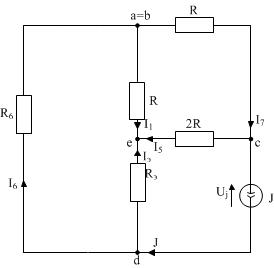 Оставляем только источник тока как на рисунке 20:
Оставляем только источник тока как на рисунке 20:
| Рисунок 20 |
| Рисунок 21 |
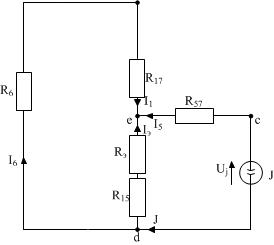 Имеем схему как на рисунке 21:
Имеем схему как на рисунке 21: Для преобразованной схемы имеем:
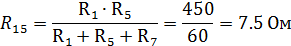
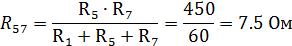
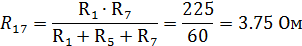
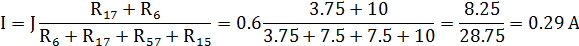
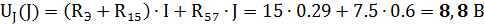
Результирующее напряжение:
UJ = UJ(E1) + UJ(E2) + UJ(EЭ) + UJ(J) = -21.9+5.2-10.1+8.8= - 18 В
Погрешность расчета составляет допустимую величину:
σU= 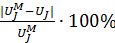 =
= 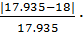 100% = 0.3%
100% = 0.3%
Задание 3.5
