Курс 2 семестр 2011-2012 учебный год
Вопросы к экзамену по математическому анализу
для студентов ИЭиФ направление «Экономика»
курс 2 семестр 2011-2012 учебный год
1. Понятие функции нескольких переменных. Область определения функции нескольких переменных и ее геометрическая интерпретация.
2. Геометрическое изображение функции двух переменных. Линии уровня.
3. Частные производные первого порядка. Производная по направлению. Градиент.
4. Полный дифференциал. Применение полного дифференциала к приближенным вычислениям.
5. Частные производные высших порядков. Экстремумы функций нескольких переменных. Условный экстремум функции нескольких переменных. Схема исследования на экстремум функции двух переменных.
6. Обыкновенные дифференциальные уравнения. Порядок, общее и частное решение дифференциального уравнения. Задача Коши.
7. Дифференциальные уравнения первого порядка. Общее решение, частное решение
8. Дифференциального уравнения первого порядка. Уравнения с разделенными переменными. Уравнения с разделяющимися переменными.
9. Однородные функции. Однородные дифференциальные уравнения первого порядка, их решения.
10. Линейные уравнения первого порядка, их решения. Метод Бернулли. Метод Лагранжа.
11. Уравнение Бернулли, методы решение.
12. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
13. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
14. Линейные неоднородные дифференциальные уравнения второго порядка с
постоянными коэффициентами со специальное правой частью.
15. Числовой ряд, его сумма. Сходимость ряда.
16. Свойства сходящихся рядов.
17. Необходимый признак сходимости. Следствие из необходимого признака сходимости.
18. Знакоположительные ряды. Признак сравнения. Признак сравнения в предельной форме. Признак Даламбера. Радикальный признак Коши.
19. Знакочередующиеся ряды. Признак Лейбница.
20. Условная и абсолютная сходимость знакочередующегося ряда.
21. Функциональные ряды и их область сходимости.
22. Степенные ряды. Радиус и область сходимости степенного ряда. Свойства степенных рядов.
23. Разложение функции в степенной ряд. Ряды Тейлора и Маклорена. Необходимое и достаточное условие сходимости ряда Тейлора функции f(x).
24. Разложение функций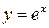 
; 
; 
; 
; 
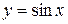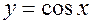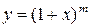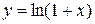в ряд Маклорена.
25. Применение степенных рядов в приближенных вычислениях значений тригонометрических функций, логарифмов.
26. Вычисление определенных интегралов при помощи степенных рядов.
27. Интегрирование дифференциальных уравнений с помощью степенных рядов.