Жиынтықты тізбектер және олардың негізгі қасиеттері
Монотонды тізбектер саны. е- саны.
e саны.  функциясының
функциясының  шегі
шегі
Жалпы мүшесі  түрінде берілген сан тізбегінің шегін e саны деп атайды, яғни
түрінде берілген сан тізбегінің шегін e саны деп атайды, яғни  . e-саны иррационал сан және оның жуық мәнімынадай e =2.71828128.... .
. e-саны иррационал сан және оның жуық мәнімынадай e =2.71828128.... .
Теорема.  . (**)
. (**)
(**)-формуласын 2-ші тамаша шек деп атайды.
Егерде (**) формулада  десек, онда х®¥ Þ a®0 (a¹0) болады да, ол формуланы былай жазуға болады:
десек, онда х®¥ Þ a®0 (a¹0) болады да, ол формуланы былай жазуға болады:  . e-cанын пайдаланып шығарылатын кейбір шектерді келтірейік:
. e-cанын пайдаланып шығарылатын кейбір шектерді келтірейік:
1)  .
.
2)  e
e  .
.
3)  .
.
3')  .
.
4) 
5) 
6) 

Егерде  шегін
шегін  және
және  болған жағдайда есептеп шығару керек болса, онда
болған жағдайда есептеп шығару керек болса, онда  түріндегі анықталмағандық алар едік.
түріндегі анықталмағандық алар едік.
Бұл секілді анықталмағандықтарды ашу үшін, берілген функцияның  негізі мен дәреже көрсеткішін мына формуланы
негізі мен дәреже көрсеткішін мына формуланы  қолдану мүмкін болатындай етіп түрлендіру керек .
қолдану мүмкін болатындай етіп түрлендіру керек .
Мысалы.
 .
.
Осыдан,  ,
,  жағдайда, мына формула табылады
жағдайда, мына формула табылады  (бұл жерде үзіліссіз функциялардыңкомпозициясының үзіліссіздігіпайдаланылды).
(бұл жерде үзіліссіз функциялардыңкомпозициясының үзіліссіздігіпайдаланылды).
Мысал келтірейік,
 .
.
Ескерту. Егер логарифмдердің негізін e деп алсақ, мұндай логарифмдер натуралдықлогарифмдер, не неперлік логарифмдер делінеді. Непер (1550-1617)- логарифм кестелерін алғашқы жасаушылардың бірі.
Егер х=ey болса, y-ті х санының натуралдық логарифмі дейді, y=lnx деп жазады (y=logex деудің орнына).
Бір санның ондық логарифмі мен натуралдық логарифмдерінің байланысын былай табады.
Егер y=lgx, не х=10y болса, оны е негізінде логарифмдесек lnx=y×ln10, 
 .
.
Егер  десек, lgx=М×lnx болады. М-ауысу модулі деп аталады.
десек, lgx=М×lnx болады. М-ауысу модулі деп аталады.
Осылайша, егер санның натуралдық логарифмі белгілі болса, онда оның ондық логарифмін ауысу модуліне көбейту арқылы табады.
Функцияның шегі.
Анықтама. 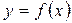 функциясы
функциясы  нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін dоң саны табылып, x -тің
нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін dоң саны табылып, x -тің 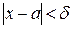 теңсіздігін қанағаттандыратын барлық мәндеріүшін, мына
теңсіздігін қанағаттандыратын барлық мәндеріүшін, мына 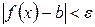 теңсіздік орындалса,
теңсіздік орындалса, 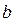 шамасы
шамасы 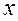 -тің
-тің 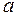 -ға ұмтылғандағы
-ға ұмтылғандағы 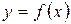 функциясының (
функциясының ( 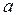 нүктесіндегі ) шегі деп аталады.
нүктесіндегі ) шегі деп аталады.
Осы анықтамадағы 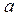 шамасының функцияның анықталу облысына кіруішарт емес, бірақ
шамасының функцияның анықталу облысына кіруішарт емес, бірақ 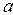 -ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруішарт.
-ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруішарт.
Егер 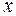 шамасы
шамасы 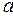 -ға ұмтылғанда,
-ға ұмтылғанда, 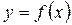 функциясының мәні
функциясының мәні 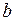 -ға ұмтылса, оны былайша жазатын боламыз
-ға ұмтылса, оны былайша жазатын боламыз
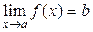 .
.
Анықтамадағы  және
және 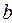 шамалары сан болуы да, не ±¥ болуы да мүмкін.
шамалары сан болуы да, не ±¥ болуы да мүмкін.
Егер 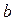 -ның шамасы
-ның шамасы 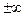 символдарының бірі болса,
символдарының бірі болса, 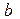 - шексіз үлкен деп аталады, мұны былай жазамыз
- шексіз үлкен деп аталады, мұны былай жазамыз
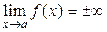 .
.
Егер әрбір e>0 үшін 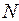 саны табылып,
саны табылып, 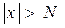 үлкен болғанда
үлкен болғанда 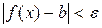 теңсіздігі орындалса,
теңсіздігі орындалса, 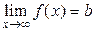 деп жазамыз.
деп жазамыз.
Егер  -ның шамасы
-ның шамасы 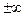 символдарының бірі болса,
символдарының бірі болса, 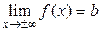 деп жазамыз.
деп жазамыз.
Ендіфункцияның шегінің геометриялық мағынасын анықтайық. Айталық 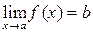 делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып,
делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып, 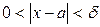 теңсіздіктерін қанағаттандыратын барлық
теңсіздіктерін қанағаттандыратын барлық 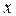 үшін
үшін 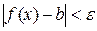 теңсіздігі орындалады деген сөз.
теңсіздігі орындалады деген сөз.
Басқаша айтқанда: аргумент x-тің 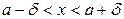 теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері
теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері 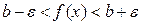 теңсіздігін қанағаттандыруы тиіс. b-саны
теңсіздігін қанағаттандыруы тиіс. b-саны 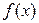 функциясының х шамасы
функциясының х шамасы  -ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады.
-ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады. 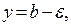
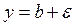 түзулер шектеген алап қандай болса да,
түзулер шектеген алап қандай болса да, 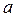 нүктесінің төңірегіне
нүктесінің төңірегіне 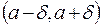 маңайын салуға болады (яғни d>0 саны табылады). Олай болса, абсциссалары
маңайын салуға болады (яғни d>0 саны табылады). Олай болса, абсциссалары 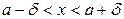 теңсіздіктерінқанағаттандыратын
теңсіздіктерінқанағаттандыратын 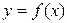 қисығының барлық нүктелері
қисығының барлық нүктелері
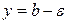 ,
, 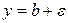 түзулері шектеде жатады (тек абсциссасы
түзулері шектеде жатады (тек абсциссасы  -ға тең нүкте ғана алапқа енбей қалуы мүмкін). Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
-ға тең нүкте ғана алапқа енбей қалуы мүмкін). Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
1) 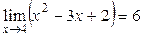 болатынын көрсету керек.
болатынын көрсету керек.
Алдын ала e>0 саны берілсін. Оған сәйкес  -тің
-тің
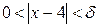 (*)
(*)
теңсіздігін қанағаттандыратын барлық мәндері үшін
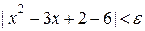 (**)
(**)
теңсіздігі, яғни 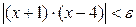 теңсіздігі орындалатын d>0 санын табайық. Ал (*)-дан
теңсіздігі орындалатын d>0 санын табайық. Ал (*)-дан 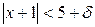 теңсіздігі шығады. Демек,
теңсіздігі шығады. Демек,
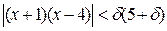 . (***)
. (***)
(**) мен (***)-дан мына қорытындыға келеміз: егер d санын d(5+d)=e тендігін қанағаттандыратын етіп алсақ, (*) теңсіздігіорындалысымен (***) да орындалады.
Сонымен, 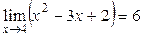 екендігі дәлелденеді.
екендігі дәлелденеді.
2) 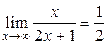 екендігін дәлелдеу керек.
екендігін дәлелдеу керек.
Алдын ала e>0 cаны берілген делік. Сонда аргумент 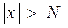 теңсіздігін қанағаттандырысымен
теңсіздігін қанағаттандырысымен 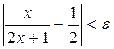 теңсіздігіорындалатындай N санын іздеуіміз керек.
теңсіздігіорындалатындай N санын іздеуіміз керек.
Ал, 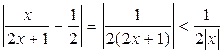 . Cондықтан
. Cондықтан 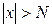 болғанда
болғанда 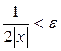 теңсіздігі орындалады. Бұдан
теңсіздігі орындалады. Бұдан 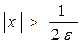 . Демек, егер
. Демек, егер 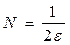 деп алсақ,
деп алсақ, 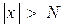 болғанда
болғанда 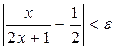 теңсіздігіорындалатыны, яғни
теңсіздігіорындалатыны, яғни 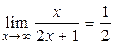 болатыны айқын.
болатыны айқын.
Ескерту. Егер  функциясы
функциясы 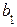 шамасына ұмтылғанда, x-тің
шамасына ұмтылғанда, x-тің  -ға ұмтылуы тек
-ға ұмтылуы тек  -дан кіші мәндер қабылдау арқылы ғана болса, былай жазып
-дан кіші мәндер қабылдау арқылы ғана болса, былай жазып 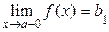 ,
, 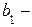 ді функцияның
ді функцияның 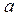 нүктесіндегі сол жақты шегі дейді.
нүктесіндегі сол жақты шегі дейді.
Егер х тек  -дан үлкен мәндер қабылдайтын болса, былай жазып
-дан үлкен мәндер қабылдайтын болса, былай жазып 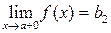 ,
, 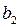 -ні функцияның
-ні функцияның  нүктесіндегі оң жақты шегі дейді.
нүктесіндегі оң жақты шегі дейді.
Ескерту. Егер аргумент х-тің берілген анықталу облысындағы барлық мәндері үшін 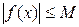 теңсіздігіорындалатындай М саны табылса,
теңсіздігіорындалатындай М саны табылса, 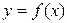 функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция
функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция 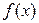 берілген облыста шектелмеген делінеді.
берілген облыста шектелмеген делінеді.
Функцияның шегі
Анықтама. 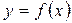 функциясы
функциясы  нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін d оң саны табылып, x -тің
нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін d оң саны табылып, x -тің 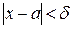 теңсіздігін қанағаттандыратын барлық мәндері үшін, мына
теңсіздігін қанағаттандыратын барлық мәндері үшін, мына 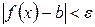 теңсіздік орындалса,
теңсіздік орындалса, 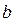 шамасы
шамасы 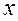 -тің
-тің 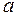 -ға ұмтылғандағы
-ға ұмтылғандағы 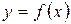 функциясының (
функциясының ( 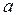 нүктесіндегі ) шегі деп аталады.
нүктесіндегі ) шегі деп аталады.
Осы анықтамадағы 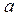 шамасының функцияның анықталу облысына кіруі шарт емес, бірақ
шамасының функцияның анықталу облысына кіруі шарт емес, бірақ 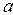 -ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруі шарт.
-ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруі шарт.
Егер 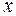 шамасы
шамасы 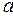 -ға ұмтылғанда,
-ға ұмтылғанда, 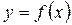 функциясының мәні
функциясының мәні 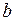 -ға ұмтылса, оны былайша жазатын боламыз
-ға ұмтылса, оны былайша жазатын боламыз
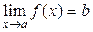 .
.
Анықтамадағы  және
және 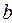 шамалары сан болуы да, не ±¥ болуы да мүмкін.
шамалары сан болуы да, не ±¥ болуы да мүмкін.
Егер 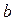 -ның шамасы
-ның шамасы 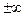 символдарының бірі болса,
символдарының бірі болса, 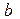 - шексіз үлкен деп аталады, мұны былай жазамыз
- шексіз үлкен деп аталады, мұны былай жазамыз
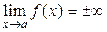 .
.
Егер әрбір e>0 үшін 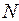 саны табылып,
саны табылып, 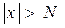 үлкен болғанда
үлкен болғанда 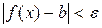 теңсіздігі орындалса,
теңсіздігі орындалса, 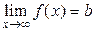 деп жазамыз.
деп жазамыз.
Егер  -ның шамасы
-ның шамасы 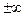 символдарының бірі болса,
символдарының бірі болса, 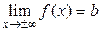 деп жазамыз.
деп жазамыз.
Ендіфункцияның шегінің геометриялық мағынасын анықтайық. Айталық 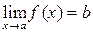 делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып,
делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып, 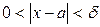 теңсіздіктерін қанағаттандыратын барлық
теңсіздіктерін қанағаттандыратын барлық 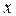 үшін
үшін 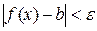 теңсіздігі орындалады деген сөз.
теңсіздігі орындалады деген сөз.
Басқаша айтқанда: аргумент x-тің 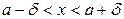 теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері
теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері 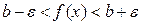 теңсіздігін қанағаттандыруы тиіс. b-саны
теңсіздігін қанағаттандыруы тиіс. b-саны 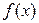 функциясының х шамасы
функциясының х шамасы  -ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады.
-ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады. 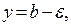
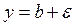 түзулер шектеген алап қандай болса да,
түзулер шектеген алап қандай болса да, 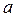 нүктесінің төңірегіне
нүктесінің төңірегіне 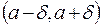 маңайын салуға болады (яғни d>0 саны табылады). Олай болса, абсциссалары
маңайын салуға болады (яғни d>0 саны табылады). Олай болса, абсциссалары 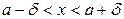 теңсіздіктерін қанағаттандыратын
теңсіздіктерін қанағаттандыратын 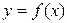 қисығының барлықнүктелері
қисығының барлықнүктелері 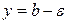 ,
, 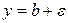 түзулері шектеген алаптың ішінде жатады (тек абсциссасы
түзулері шектеген алаптың ішінде жатады (тек абсциссасы  -ға тең нүкте ғана алапқа енбей қалуы мүмкін). Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
-ға тең нүкте ғана алапқа енбей қалуы мүмкін). Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
1) 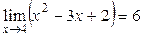 болатынын көрсету керек.
болатынын көрсету керек.
Алдын ала e>0 саны берілсін. Оған сәйкес  -тің
-тің
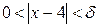 (*)
(*)
теңсіздігін қанағаттандыратын барлық мәндері үшін
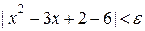 (**)
(**)
теңсіздігі, яғни 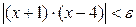 теңсіздігі орындалатын d>0 санын табайық. Ал (*)-дан
теңсіздігі орындалатын d>0 санын табайық. Ал (*)-дан 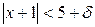 теңсіздігі шығады. Демек,
теңсіздігі шығады. Демек,
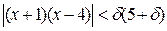 . (***)
. (***)
(**) мен (***)-дан мына қорытындыға келеміз: егер d санын d(5+d)=e тендігін қанағаттандыратын етіп алсақ, (*) теңсіздігіорындалысымен (***) да орындалады.
Сонымен, 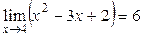 екендігі дәлелденеді.
екендігі дәлелденеді.
2) 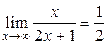 екендігін дәлелдеу керек.
екендігін дәлелдеу керек.
Алдын ала e>0 cаны берілген делік. Сонда аргумент 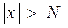 теңсіздігін қанағаттандырысымен
теңсіздігін қанағаттандырысымен 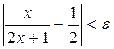 теңсіздігіорындалатындай N санын іздеуіміз керек.
теңсіздігіорындалатындай N санын іздеуіміз керек.
Ал, 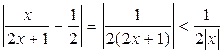 . Cондықтан
. Cондықтан 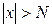 болғанда
болғанда 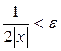 теңсіздігі орындалады. Бұдан
теңсіздігі орындалады. Бұдан 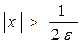 . Демек, егер
. Демек, егер 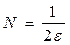 деп алсақ,
деп алсақ, 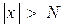 болғанда
болғанда 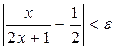 теңсіздігі орындалатыны, яғни
теңсіздігі орындалатыны, яғни 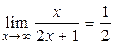 болатыны айқын.
болатыны айқын.
Ескерту. Егер 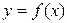 функциясы
функциясы 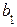 шамасына ұмтылғанда, x-тің
шамасына ұмтылғанда, x-тің  -ға ұмтылуы тек
-ға ұмтылуы тек  -дан кіші мәндер қабылдау арқылы ғана болса, былай жазып
-дан кіші мәндер қабылдау арқылы ғана болса, былай жазып 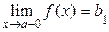 ,
, 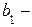 ді функцияның
ді функцияның 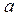 нүктесіндегі сол жақты шегі дейді.
нүктесіндегі сол жақты шегі дейді.
Егер х тек  -дан үлкен мәндер қабылдайтын болса, былай жазып
-дан үлкен мәндер қабылдайтын болса, былай жазып 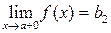 ,
, 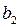 -ні функцияның
-ні функцияның  нүктесіндегі оң жақты шегі дейді.
нүктесіндегі оң жақты шегі дейді.
Ескерту. Егер аргумент х-тің берілген анықталу облысындағы барлық мәндері үшін 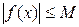 теңсіздігіорындалатындай М саны табылса,
теңсіздігіорындалатындай М саны табылса, 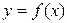 функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция
функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция 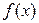 берілген облыста шектелмеген делінеді.
берілген облыста шектелмеген делінеді.
Шексіз аз шама және оның қасиеттері
Анықтама. Егер 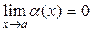 не
не 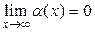 болса,
болса, 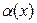 функциясы
функциясы 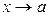 не x®¥ болғанда шексіз аз шама делінеді.
не x®¥ болғанда шексіз аз шама делінеді.
Шектің анықтамасына сүйеніп, жоғарыдағы анықтаманы былайша тұжырымдауға болады: алдынала берілген кез-келген жеткілікті аз e>0 саны үшін 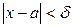 теңсіздігі орындалатынx -тың мәндері үшін
теңсіздігі орындалатынx -тың мәндері үшін 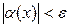 теңсіздігі орындалатындай d саны табылса, a(x) шексіз аз шама делінеді (x®
теңсіздігі орындалатындай d саны табылса, a(x) шексіз аз шама делінеді (x®  ).
).
Мысалы.
1) функция a(x)=(x-2)2, x шамасы 2-ге ұмтылғанда шексіз аз шама, өйткені 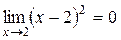 .
.
2) функция a(x)= 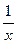 , х®¥ болғанда шексіз аз шама, өйткені
, х®¥ болғанда шексіз аз шама, өйткені 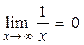 .
.
Теорема. Егер 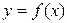 функциясы b санымен шексіз аз шама a-нің қосындысына тең болса, яғни y=b+a болса, lіm y=b (x®a не х®¥) болады. Керісінше, егер
функциясы b санымен шексіз аз шама a-нің қосындысына тең болса, яғни y=b+a болса, lіm y=b (x®a не х®¥) болады. Керісінше, егер 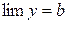 болса,
болса, 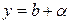 деп жазуға болады. Мұндағы a шексіз аз шама.
деп жазуға болады. Мұндағы a шексіз аз шама.
Теорема. Егер  шамасы
шамасы  -ға ұмтылғанда a(x) нольге ұмтылса, y=
-ға ұмтылғанда a(x) нольге ұмтылса, y= 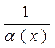 шексіз үлкен шамаға ұмтылады.
шексіз үлкен шамаға ұмтылады.
Теорема. Бірнеше (саны шектеулі) шексіз аз шамалардың алгебралық қосындысы шексіз аз шама болады.
Теорема. Шексіз аз шама a(x)-тың шектелген g(x) функциясына көбейтіндісі (x®  , x®¥) шексіз аз шама.
, x®¥) шексіз аз шама.
Салдар. Егер lіm a(x)=0, lіm b(x)=0 болса, lіmab=0.
Салдар. Егер lіm a(x)=0, c=const болса, lіm ca=0.
Теорема. Егер lіma(x)=0, lіmb(x)¹0 болса a(x)·b-1(x)-шексіз аз шама болады.
Шектер туралы негізгі теоремалар
Теорема. Бірнеше (саны шектеулі) функциялардың қосындысының шегі сол функциялардың шектерінің қосындысына тең
lіm(u1+u2+. . .+u k) = lіm u1+lіm u2+. . .+lіm u k .
Теорема. Бірнеше (саны шектеулі) айнымалы шамалардыңкөбейтіндісінің шегі сол шамалардың шектерініңкөбейтіндісіне тең:
lіm(u1u2. . .u k)=lіm u1lіm u2. . . lіm u k .
Теорема. 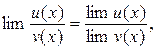
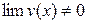 .
.
Теорема. Егер u(x), 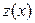 және v(x) функцияларының сәйкес мәндері мына
және v(x) функцияларының сәйкес мәндері мына 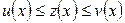 теңсіздіктерін қанағаттандырса және u(x) пен v(x) функциялары
теңсіздіктерін қанағаттандырса және u(x) пен v(x) функциялары 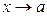 не
не 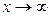 -да бір b санына ұмтылса, онда
-да бір b санына ұмтылса, онда 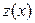 -те сол шекке ұмтылады.
-те сол шекке ұмтылады.
Теорема. Егер  шамасы
шамасы  -ға (не ¥-ке) ұмтылғанда теріс емес
-ға (не ¥-ке) ұмтылғанда теріс емес 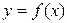 функциясы
функциясы 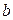 шегіне ұмтылса, онда
шегіне ұмтылса, онда 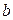 -нольден кіші болмайды.
-нольден кіші болмайды.
Теорема. Егер үдемелі айнымалы шама 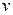 шектелген шама, яғни
шектелген шама, яғни 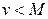 болса, онда бұл айнымалы шаманың шегі бар, яғни
болса, онда бұл айнымалы шаманың шегі бар, яғни 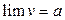 болады және ол
болады және ол 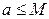 .
.
Кемімелі айнымалы шама үшін де осыған ұқсас теорема орындалады.
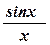 функциясының
функциясының 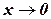 шегі
шегі
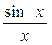 функциясы
функциясы 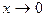 да
да 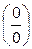 түріндегі анықталмағандықты береді.
түріндегі анықталмағандықты береді.
Теорема. 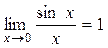 . (*)
. (*)
(*) формуласын 1-ші тамаша шек деп атайды.
Есеп шығарғанда, бізге қажет болатын маңызы зор бірнеше шектерді (бірінші тамаша шектің көмегімен дәлелденетін) келтірейік:
1) 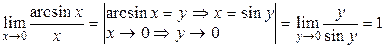 .
.
2) 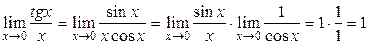 .
.
3) 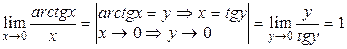 .
.
