Автоматтардың pumping туралы теоремасы.

Тілдің регулярлы болуы оның қандай да бір ақырлы детерменистік автомат қабылданылуымен пара пар. Мұнда М-нің күйлерінің саны ақырлы. Мысалға n дана.

Рumping туралы теоремасы.L-регулярлы жиын болсын, онда саны бар болып, егер -кез келген сөз үшін , оны түрінде жазуға болады. мұндағы әрі кез келген үшін .

Рumping туралы теоремадан: егер бір регулярлы жиында жеткілікті ұзындықта

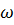сөзі бар болса, онда осы жиын сөзін де қамтитын шексіз жиын дегенді түсінуге болады.

Рumping туралы теорема қолданылуы.Ойын ретінде қарастырсақ: сіз ж/е тағы бір адам бар, негізгі мақсат сіздің оны жеңуіңіз.

1. Сіз регулярлы емес деп ойлаған бір L тілін таңдап алыңыз.

2. Қарсы жақ n санын таңдап алу керек, яғни Рumping туралы теоремадағы тұрақты сан n. Енді кез келген таңдап алынған n санына дайын болу керек, бірақ бір жақсы жері қарсы жағың бір рет n санын таңдап алғаннан кейін ол оны өзгерте алмайды. Дегенмен қарсы жақты өте осал деп санамау керек.

3. Енді сіз осы L тіліне тиісті бір сөздер тізбегі 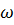-ны алыңыз. Сіздің таңдап алған 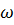қарсы жағың таңдап алған n санымен іштей байланыста.

4. Қарсы жағың Сіз берге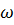н сөзін 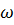=xyz түрінде жіктеп жазылуы керек, яғни x,y,z-ішкі сөзін белгілеу керек. Әрі олар шартын қанағаттандыруы шарт.

5. Сіз енді Рumping туралы теореманыңтұжырымына қайшы қорытындыға келтіруіңіз керек, ол үшін кез келген анықталған x,y,z ішкі сөздер үшін қандай да бір бар болып шартын қанағаттандыратын t санын табу керек.

Майхилл-Нероуд теоремасы.

Майхилла-Нероудтың теоремасының формалды тiлдерiнiң теорияларында қажеттi және тiлдiң жүйелiлiгiнiң жеткiлiктi шарттарын анықтайды. Сонымен бiрге осы теорема осы тiлді жүйелi дәлелдеуге мүмкiндiк бередi.

Теорема (Майхилл-Нероуд): егер - регуляр тіл болса, онда DFA- L тілін анықтайтын автомат табылып, автоматтың күйлер саны L тілі бойынша эквивалент кластар санына тең.

V алфавитінде L тілі берілсін, ≡L қатынасы алфавиттегі бүкіл сөздер жиынына берілген.

X ≡L y болады сонда ж/е тек сонда ғана,егер барлық берілген алфавитке тиісті z үшін, xz ж/е yz сөздері L тілдеріне тиісті немесе бір уақытта тиісті емес болса. ≡L-Vалфавитіндегі сөздер жиынының эквивалентті қатынасы екенін дәлелдей аламыз. Майхилл Нероуд теоремасы б/ша минималды DFA-та, L-тіл бар, ≡L қатынасынасы б/ша эквивалентті класс санына тең. Берілген қатынас сонымен қатар бинарлы қатынастардағы индексі деп аталады, ind≡L деп белгіленеді.

Майхил-Нероуд теоремасынан эквивалентті кластар саны ақырлы болған кезде ғана тіл регулярлы болатындығы шығады. Егер қатынас шексіз эквивалентті кластар санында тілді бұзса тіл регулярлы болмайды. Бұл тұжырым регуляр емес тілдерді анықтағанда жиі қолданылады.

13. Майхилл-Нероуд теоремасының салдары(регуляр емес тілдер туралы)

L тілі регуляр болады сонда және тек сонда ғана егер тілі бойынша анықталған эквивалент класстар саны ақырлы болса. Дәлелдеу: Егер L тілі регуляр болса, онда L кейбір ақырлы автоматтар үшін және -де эквиваленттік класстардан аз емес күй сақтайды. Демек в эквивалентті класстардың ақырлы саны. Бұл салдар арқылы тілдің регуляр емес екендігін де дәлелдеуге болады. Мысалы: L={ }

Ешқандай екі сөз i бола тұры қатысты эквивалентті емес, себебі кейін жазылса да L тілінің сөзін береді, бірақ L тіліне жатпайтын сөзді береді. Осыдан шексіз көп эквивалентті классқа ие. Осының салдарынан L тілі регуляр емес болып шығады.