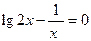Метод Золотого сечения
Еще одним методом последовательного деления отрезка, содержащего корень уравнения, является метод золотого сечения. Его смысл состоит в делении отрезка на две неравные части так, чтобы, отношение всего отрезка к большей части, равнялось отношению большей части отрезка к меньшей (принцип «золотого сечения»).
Пусть дано уравнение 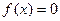 , где функция
, где функция 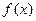 непрерывна на
непрерывна на 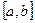 и
и 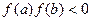 . Суть метода состоит в том, чтобы разделить отрезок
. Суть метода состоит в том, чтобы разделить отрезок 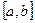 точкой
точкой 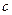 так, чтобы
так, чтобы 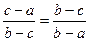 , решая это уравнение, получаем
, решая это уравнение, получаем 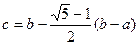 . Все остальные действия осуществляются аналогично предыдущему методу.
. Все остальные действия осуществляются аналогично предыдущему методу.
Метод рандомизации
Метод рандомизации также является методом последовательного сужения отрезка, содержащего корень уравнения. Но, в отличие от предыдущих рассмотренных методов, он не является строго детерминированным. В нем вводится элемент случайности, и точки деления отрезка выбираются в соответствии с определенным законом распределения. При этом в среднем можно получить выигрыш в числе этапов по сравнению с другими методами.
Пусть дано уравнение 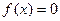 , где функция у=
, где функция у= 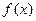 непрерывна на
непрерывна на 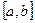 и
и 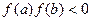 . Точку деления текущего отрезка
. Точку деления текущего отрезка 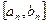 на каждом этапе находят из выражения
на каждом этапе находят из выражения 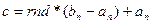 , где
, где 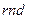 случайное число, причем
случайное число, причем 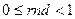 .
.
В результате получаем на каком-то этапе или точный корень исходного уравнения, или же бесконечную последовательность отрезков 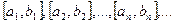 таких, что
таких, что 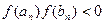 (n = 1, 2, …).
(n = 1, 2, …).
В качестве корня снова выбираем 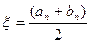 .
.
Примерный образец оформления работы
Вычислительный бланк для метода деления отрезка пополам или его модификаций:
| № | f(a) | a | b | f(b) | c=(a+b)/2 | f(c) |
Задание. Вычислить с точностью 0,001 корень уравнения 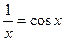 .
.
1) Отделение корня: корни данного уравнения могут быть найдены как абсциссы точек пересечения кривых 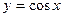 и
и 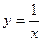 .
.
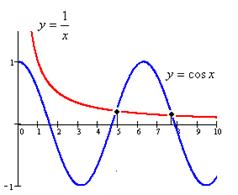
Из графика замечаем, что корни уравнения принадлежат отрезкам [4;6] и [7;8]. Уточним, например, корень, лежащий на отрезке [7;8]. Уравнение запишем в виде 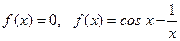 .
.
Метод половинного деления:
| № | а | в | х | f(x) |
| 1 | 7 | 8 | 7,5 | 0,21330 |
| 2 | 7,5 | 8 | 7,75 | -0,02524 |
| 3 | 7,5 | 7,75000 | 7,62500 | 0,09584 |
| 4 | 7,62500 | 7,75000 | 7,68750 | 0,03563 |
| 5 | 7,68750 | 7,75000 | 7,71875 | 0,00527 |
| 6 | 7,71875 | 7,75000 | 7,73438 | -0,00997 |
| 7 | 7,71875 | 7,73438 | 7,72656 | -0,00235 |
| 8 | 7,71875 | 7,72656 | 7,72266 | 0,00146 |
| 9 | 7,72265 | 7,72656 | 7,72460 | -0,0004 |
Корень уравнения равен
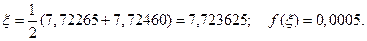
Метод Фибоначчи
| № | a:b | a | b | x | f(x) |
| 1:1 | 7,5 | 0,21330 | |||
| 1:2 | 7,5 | 7,66667 | 0,05579 | ||
| 2:3 | 7,66667 | 7,80000 | -0,07425 | ||
| 3:5 | 7,66667 | 7,8 | 7,71667 | 0,00729 | |
| 5:8 | 7,71667 | 7,8 | 7,74872 | -0,02398 | |
| 8:13 | 7,71667 | 7,74872 | 7,72888 | -0,00461 | |
| 13:21 | 7,71667 | 7,72888 | 7,72134 | 0,00275 | |
| 21:34 | 7,72113 | 7,72887 | 7,72421 | -0,00005 |
Корень уравнения равен
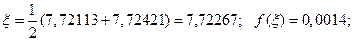
Метод Золотого сечения
| № | a | b | c | f(c) |
| 7,381966 | 0,31922 | |||
| 7,381966 | 7,618034 | 0,10250 | ||
| 7,618034 | 7,763932 | -0,03887 | ||
| 7,618034 | 7,763932 | 7,673762 | 0,04893 | |
| 7,673762 | 7,763932 | 7,708204 | 0,01553 | |
| 7,708204 | 7,763932 | 7,729490 | -0,00520 | |
| 7,708204 | 7,729490 | 7,716335 | 0,00762 | |
| 7,716335 | 7,729490 | 7,721360 | 0,00272 | |
| 7,721359 | 7,729490 | 7,724465 | -0,00030 |
Корень уравнения равен
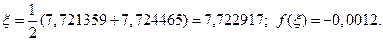
Метод рандомизации
| № | Rnd | a | b | x | f(x) |
| 0,038625 | 7,038625 | 0,58590 | |||
| 0,845374 | 7,038625 | 7,851347 | -0,12473 | ||
| 0,986774 | 7,038625 | 7,851347 | 7,840598 | -0,11416 | |
| 0,502909 | 7,038625 | 7,840598 | 7,441944 | 0,26610 | |
| 0,292490 | 7,441944 | 7,840598 | 7,558546 | 0,15886 | |
| 0,504041 | 7,558546 | 7,840598 | 7,700712 | 0,02281 | |
| 0,427129 | 7,700712 | 7,840598 | 7,760461 | -0,03547 | |
| 0,999532 | 7,700712 | 7,760461 | 7,760433 | -0,03545 | |
| 0,839071 | 7,700712 | 7,760433 | 7,750822 | -0,02604 | |
| 0,097017 | 7,700712 | 7,750822 | 7,705573 | 0,01809 | |
| 0,721382 | 7,705573 | 7,750822 | 7,738215 | -0,01372 | |
| 0,251936 | 7,705573 | 7,738215 | 7,713797 | 0,01009 | |
| 0,816922 | 7,713797 | 7,738215 | 7,733745 | -0,00936 | |
| 0,430309 | 7,713797 | 7,733745 | 7,722381 | 0,00173 | |
| 0,176364 | 7,722381 | 7,733745 | 7,724385 | -0,00023 |
Корень уравнения равен
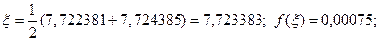
Индивидуальные варианты
1) 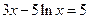 2)
2) 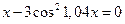 3)
3) 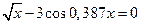 4)
4) 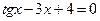 5)
5) 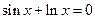 6)
6) 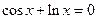 7)
7) 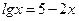 8)
8) 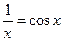
9) 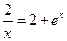 10)
10) 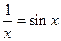 11)
11) 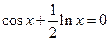 12)
12) 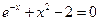
13) 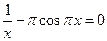 14)
14) 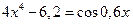 15)
15) 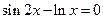 16)
16) 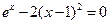
17) 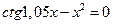 18)
18) 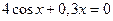 19)
19) 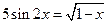 20)
20) 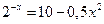
21) 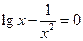 22)
22) 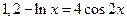 23)
23) 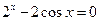 24)
24) 
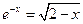
25) 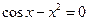 26)
26) 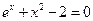 27)
27) 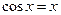 28)
28) 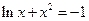
29) 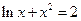 30)
30) 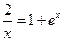 31)
31) 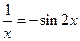 32)
32)