Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши
ЗАДАНИЕ 1
(а) Разложить функцию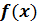 
в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию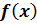 
в ряд Фурье по 
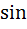кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию 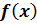в ряд Фурье по 
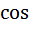кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
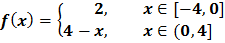
Решение:
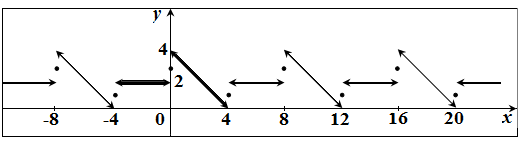
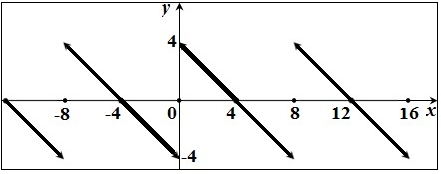
(а)Построим график функции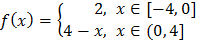 
и ее периодического продолжения 
на всю ось (график 
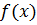выделен на рисунке жирной линией):
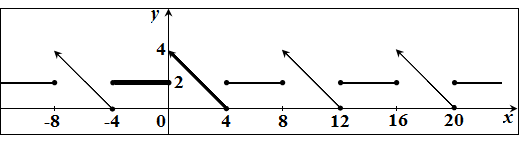
Имеем период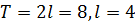 
. Тогда ряд Фурье имеет вид
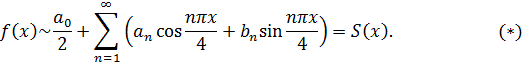
График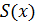 
совпадает с графиком 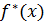в точках непрерывности, а в точках разрыва 
:
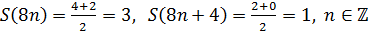Коэффициенты Фурье находим по формулам
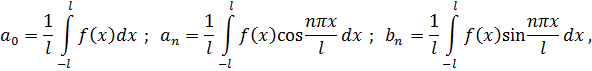
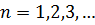
Получаем
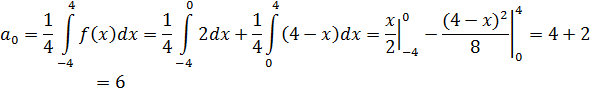
и, учитывая, что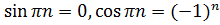 
, находим
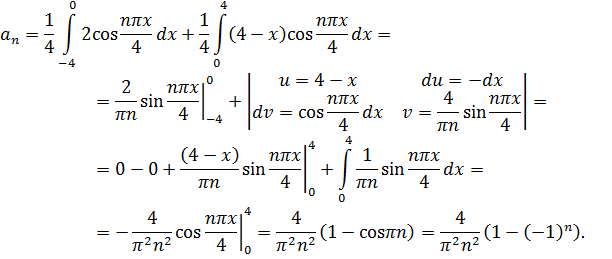
Итак,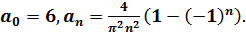 
Находим
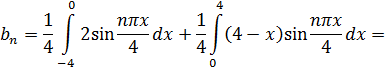
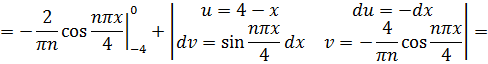
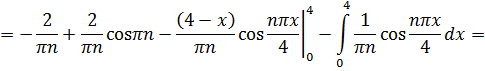
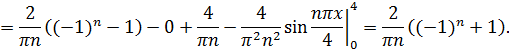
Итак,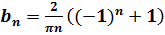 
.
Подставляем найденные коэффициенты в ряд Фурье (*), окончательно имеем:
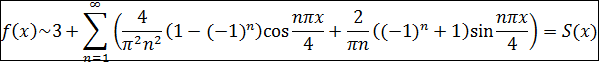
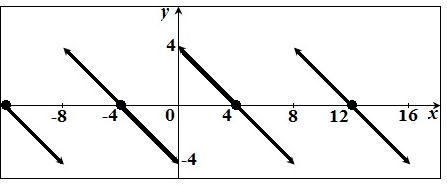
(б)Разложим функцию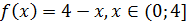 
, по синусам кратных дуг в ряд Фурье. Продолжим 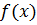нечетным образом на отрезок 
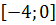, а потом периодически продолжим на всю ось:
Имеем период 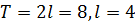. Тогда ряд Фурье по синусам имеет вид
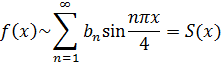
причем функция 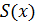совпадает с продолженной функцией 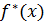в точках непрерывности, а в точках разрыва имеем 
:
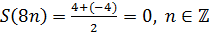Находим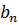 
:
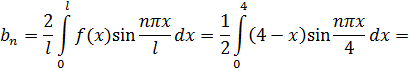
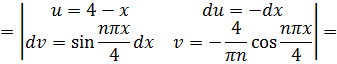
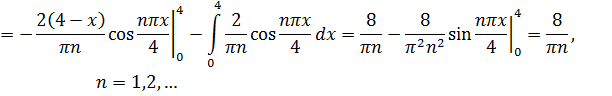
Итак,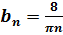 
.
Окончательно имеем
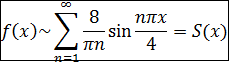
(в)Теперь разложим функцию 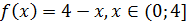, по косинусам кратных дуг в ряд Фурье. Продолжим эту функцию четным образом на отрезок 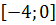, а потом периодически продолжим на всю ось, в качестве периода взяв :
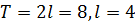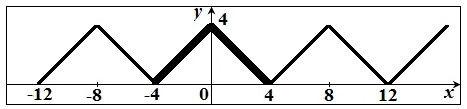
Поскольку продолженная функция 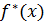непрерывна на всей числовой прямой, то сумма ряда 
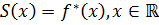,а сам ряд имеет вид:
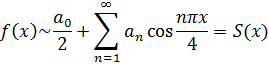
Находим коэффициенты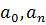 
:
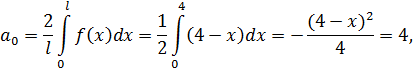
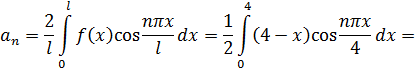
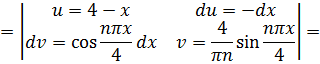
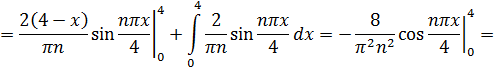
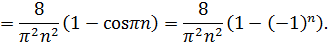
Итак,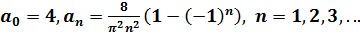 
Ряд Фурье имеет вид
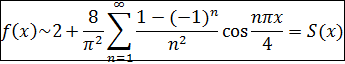
ЗАДАНИЕ 2
Найти общее решение и решение, удовлетворяющее указанным начальным условиям для квазилинейного уравнения первого порядка
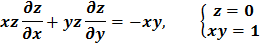
Решение:
Для решения квазилинейного уравнения в частных производных первого порядка относительно функции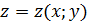 
запишем систему обыкновенных дифференциальных уравнений вида
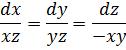
Решаем эту систему сначала для одной пары, а потом для другой пары дифференциальных уравнений.
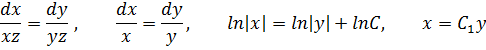
Рассмотрим другую пару
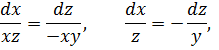
из полученного решения первой пары выражаем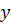 
, а именно 
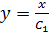, и подставляем в это уравнение
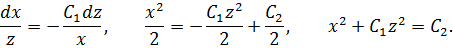
Тогда общее решение исходного уравнения имеет вид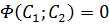 
, где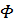 
- произвольная функция двух аргументов.
Имеем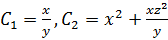 
и общее решение 
.
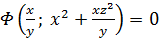Поскольку функция 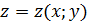входит в один из аргументов функции 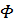, то можно выразить этот аргумент через другой с помощью произвольной функции одной переменной 
:
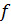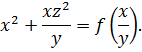
Это и есть общее решение.
Найдем вид функции 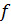из дополнительных условий 
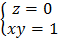. Тогда 
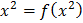, то есть 
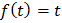. Имеем частное решение 
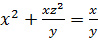или
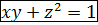
Проверка:
Функция 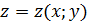задана неявно.
. 
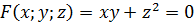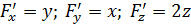
Тогда найдем
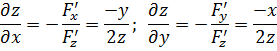
Подставим в исходное уравнение и получим тождество:
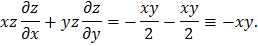
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
;
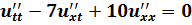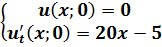
Решение:
Исходное уравнение представляет собой линейное однородное уравнение в частных производных второго порядка
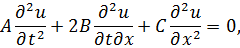
где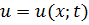 
- искомая функция, 
.
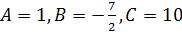Определяем тип уравнения:
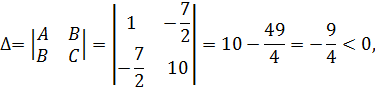
то есть это уравнение гиперболического типа. Составляем характеристическое уравнение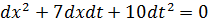 
и решаем его.
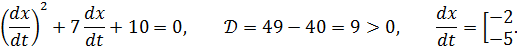
Получаем две характеристики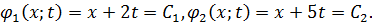 
Переходим к новым переменным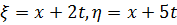 
. Тогда
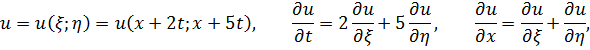
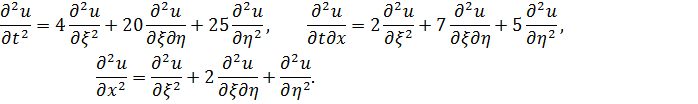
Подставим в исходное уравнение:
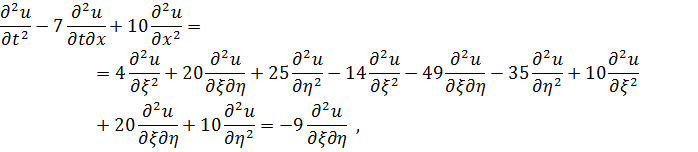
а значит, по условию
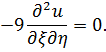
Получаем каноническое уравнение для гиперболического типа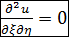 
.
Решаем это уравнение.
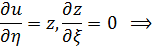
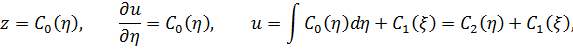
где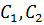 
- произвольные функции. Заменяем 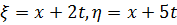и получаем общее решение 
.
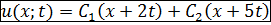Теперь решаем задачу Коши, то есть находим функции 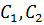из начальных условий 
.
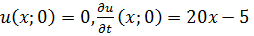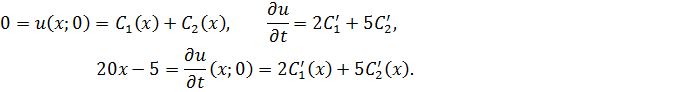
Решаем систему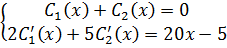 
относительно 
.
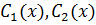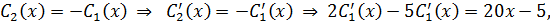
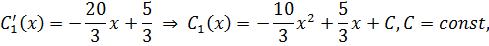
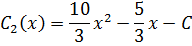
Подставим в общее решение:
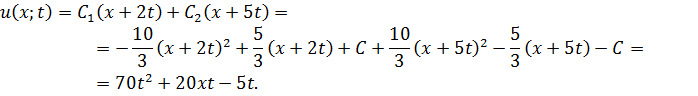
Получаем частное решение задачи Коши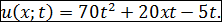 
Проверка:
Найденная функция удовлетворяет условию задачи Коши:
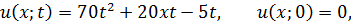
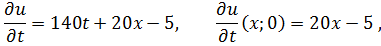
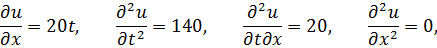
т.е.
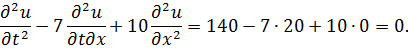
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения:
  |   |
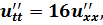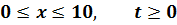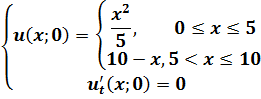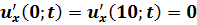Решение:
Исходное уравнение является уравнением теплопроводности. Решаем задачу с нулевыми краевыми условиями и начальными условиями (смешанная задача), для чего используем метод разделения переменных (метод Фурье).
Ищем ненулевое решение в виде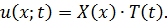 
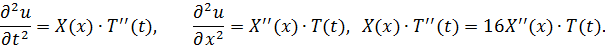
Разделяем переменные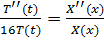 
. Так как каждая дробь зависит только от одной переменной, то их равенство означает, что они постоянные:
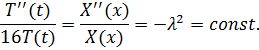
Получаем систему обыкновенных дифференциальных уравнений
Сначала решаем второе уравнение, которое должно удовлетворять краевым условиям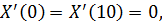 
так как
.
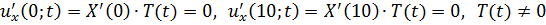Это задача Штурма-Лиувилля: найти решение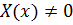 
, удовлетворяющее уравнению 
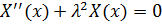и нулевым условиям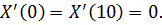 
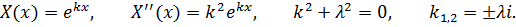
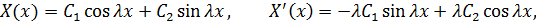
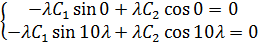
Сначала считаем, что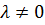 
. Тогда
.
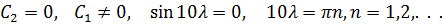Собственные значения задачи Штурма-Лиувилля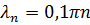 
. Находим собственные функции 
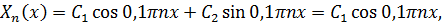так как 
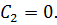Поскольку 
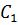- произвольная постоянная, 
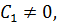возьмем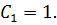 
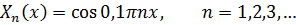
Если взять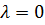 
, тогда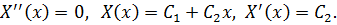 
Так как 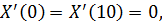то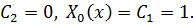 
Итак, получаем решение задачи Штурма-Лиувилля:
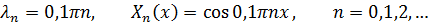
Для каждого значения 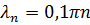решаем первое уравнение системы
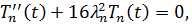
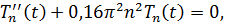
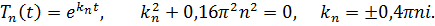
Общее решение для первого уравнения имеет вид
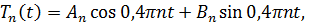
где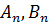 
- произвольные постоянные. Таким образом, получено решение
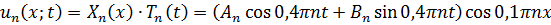
для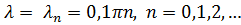 
Будем искать общее решение исходного уравнения в виде ряда:
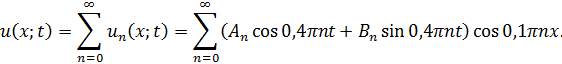
Потребуем, чтобы оно удовлетворяло начальным условиям
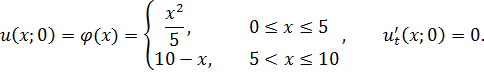
Получаем
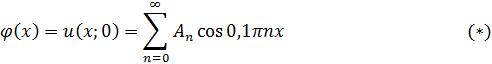
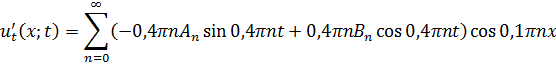
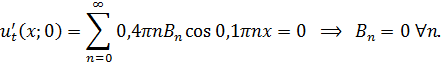
Соотношение 
представляет разложение функции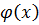 
в ряд Фурье по косинусам с периодом 
.
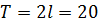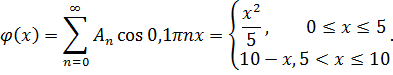
Ищем коэффициенты Фурье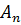 
:
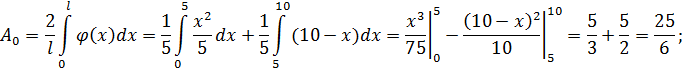
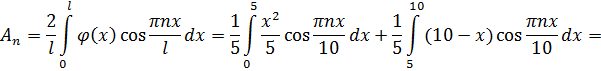
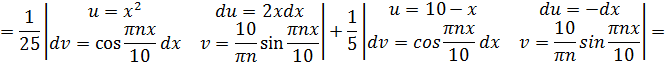
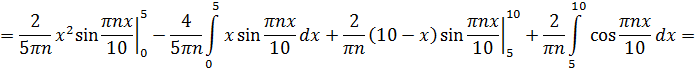
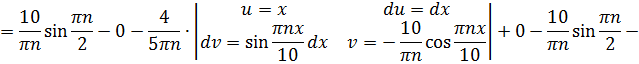
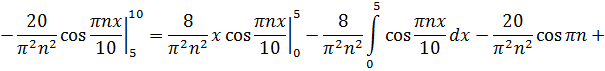
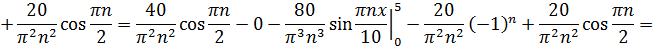
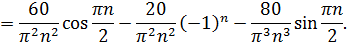
Итак, найдены коэффициенты Фурье
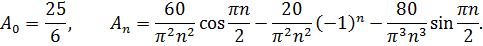
Окончательно получаем решение смешанной задачи:
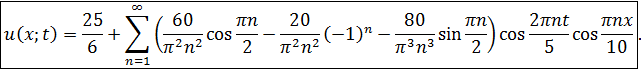
ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения (уравнения теплопроводности):
  |   |
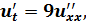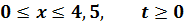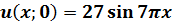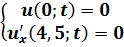Решение:
Исходное уравнение решаем методом разделения переменных (метод Фурье). Ищем ненулевое решение в виде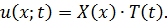
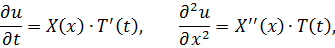
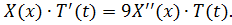
Разделяем переменные
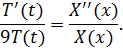
Так как каждая дробь зависит только от одной переменной, то их равенство означает, что они – постоянные (обозначим ее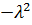 
):
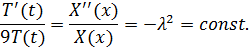
Получаем систему обыкновенных дифференциальных уравнений
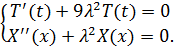
Сначала решаем второе уравнение (с учетом преобразованного на языке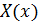 
граничного условия):
Получили задачу Штурма-Лиувилля.
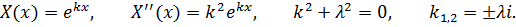
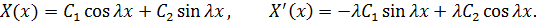
Используем краевые условия для определения :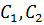
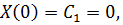
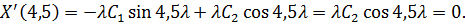
Так как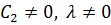 
(иначе функция 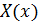станет тождественно равна нулю), то 
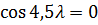, а значит 
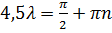, и, следовательно, собственные значения задачи Штурма-Лиувилля: 
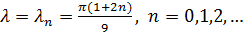. Коэффициент 
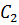является постоянной ненулевой величиной, т.е. имеем права принять ее за 1.
Находим собственные функции
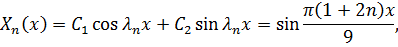
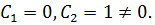
Решаем второе уравнение:
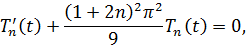
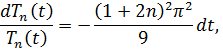
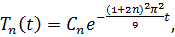
где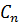 
– произвольные постоянные.
Итак, функции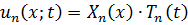 
удовлетворяют краевым условиям для 
.
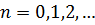Ищем общее решение в виде ряда
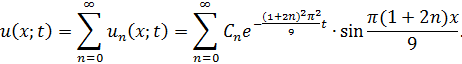
Потребуем выполнение начального условия
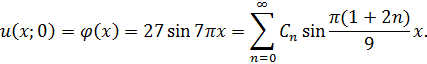
Полученное соотношение есть разложение функции 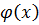в ряд Фурье по синусам. Ищем коэффициенты Фурье 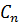этого разложения при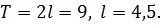 
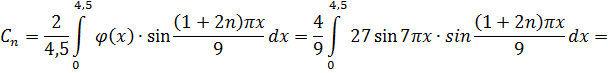
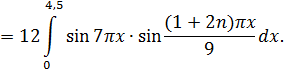
Используя свойства ортогональности тригонометрической системы, получим, что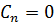 
, если 
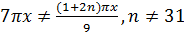, а если 
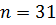, то
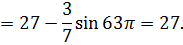
Таким образом, частное решение получаем из бесконечного ряда, в котором все слагаемые равны нулю, кроме слагаемого с номером 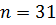и коэффициентом 
:
.
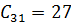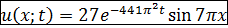ВАРИАНТ 1
ЗАДАНИЕ 1
(а) Разложить функцию 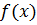в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию 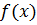в ряд Фурье по 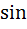кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию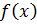 
в ряд Фурье по 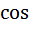кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
ЗАДАНИЕ 2
Найти общее решение или решение, удовлетворяющее указанным начальным условиям.
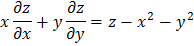
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
;
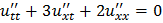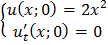
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения.
  |   |
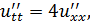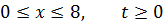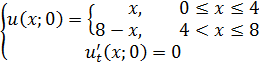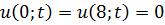ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения
  |   |
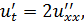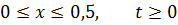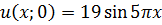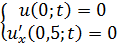ВАРИАНТ 2
ЗАДАНИЕ 1
(а) Разложить функцию 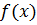в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию 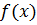в ряд Фурье по 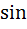кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию 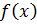в ряд Фурье по 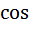кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
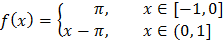
ЗАДАНИЕ 2
Найти общее решение или решение, удовлетворяющее указанным начальным условиям.
; 
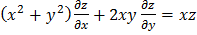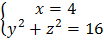
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
;
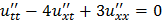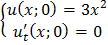
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения.
  |   |
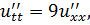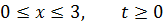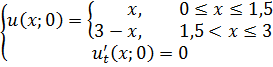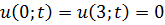ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения.
  |   |
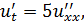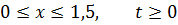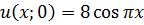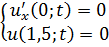ВАРИАНТ 3
ЗАДАНИЕ 1
(а) Разложить функцию 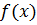в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию 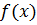в ряд Фурье по 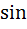кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию 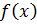в ряд Фурье по 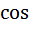кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
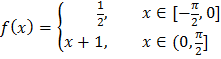
ЗАДАНИЕ 2
Найти общее решение или решение, удовлетворяющее указанным начальным условиям.
; 
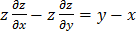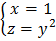
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
; 
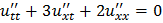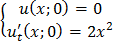
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения.
  |   |
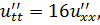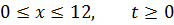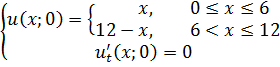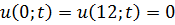ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения.
  |   |
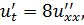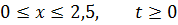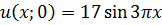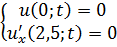ВАРИАНТ 4
ЗАДАНИЕ 1
(а) Разложить функцию 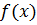в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию 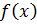в ряд Фурье по 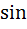кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию 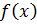в ряд Фурье по 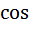кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
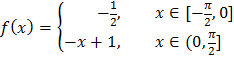
ЗАДАНИЕ 2
Найти общее решение или решение, удовлетворяющее указанным начальным условиям.
; 
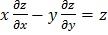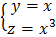
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
; 
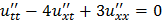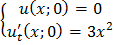
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения.
  |   |
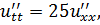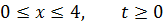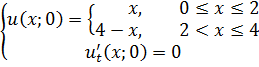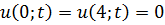ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения.
  |   |
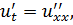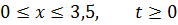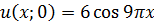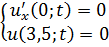ВАРИАНТ 5
ЗАДАНИЕ 1
(а) Разложить функцию 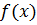в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию 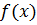в ряд Фурье по 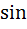кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию 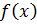в ряд Фурье по 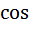кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
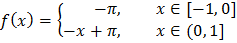
ЗАДАНИЕ 2
Найти общее решение или решение, удовлетворяющее указанным начальным условиям.
; 
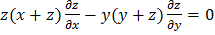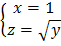
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
;
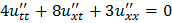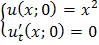
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения.
  |   |
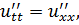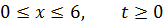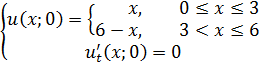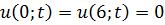ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения.
  |   |
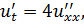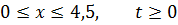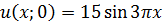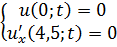ВАРИАНТ 6
ЗАДАНИЕ 1
(а) Разложить функцию 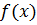в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию 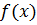в ряд Фурье по 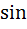кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию 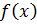в ряд Фурье по 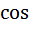кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
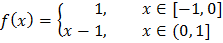
ЗАДАНИЕ 2
Найти общее решение или решение, удовлетворяющее указанным начальным условиям.
;
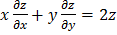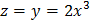
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
; 
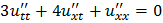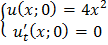
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения.
| |  |
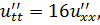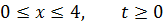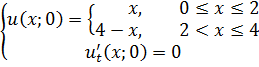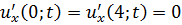ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения.
| |  |
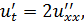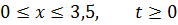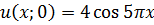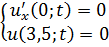ВАРИАНТ 7
ЗАДАНИЕ 1
(а) Разложить функцию 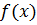в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию 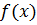в ряд Фурье по 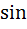кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию 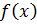в ряд Фурье по кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
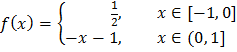
ЗАДАНИЕ 2
Найти общее решение или решение, удовлетворяющее указанным начальным условиям.
; 
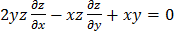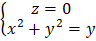
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
;
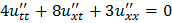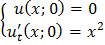
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения.
 |   |
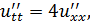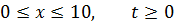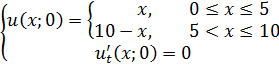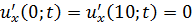ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения.
 |  |
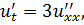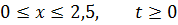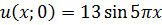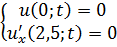ВАРИАНТ 8
ЗАДАНИЕ 1
(а) Разложить функцию 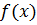в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.
(б) Разложить функцию 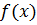в ряд Фурье по 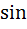кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
(в) Разложить функцию 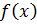в ряд Фурье по 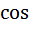кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.
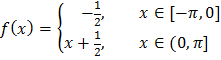
ЗАДАНИЕ 2
Найти общее решение или решение, удовлетворяющее указанным начальным условиям.
; 
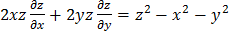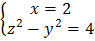
ЗАДАНИЕ 3
Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.
; 
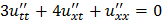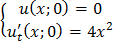
ЗАДАНИЕ 4
Методом Фурье решить смешанную задачу для гиперболического уравнения.
| |  |
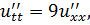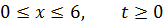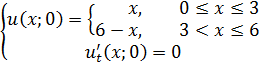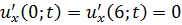ЗАДАНИЕ 5
Методом Фурье решить смешанную задачу для параболического уравнения.
| |  |
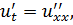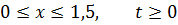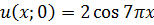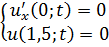