Линии влияния усилий в стержнях простейших ферм

Передача нагрузки на ферму производится в узлах-шарнирах; следовательно здесь имеет место случай узловой передачи нагрузки.

Рассмотрим следующие приемы построения линий влияния для ферм: 1) способ моментнойточки, 2) способ про­екций.

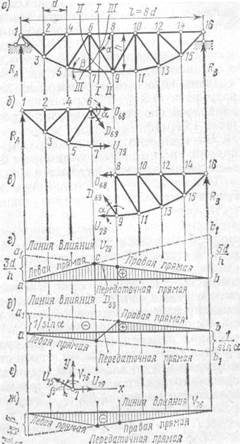
Способ моментной точ­ки.Построим линию влияния усилия в стержне 7—9 фермы, изображенной на рис. 13. Проведем разрез /—/, пересекающий три стержня.

Когда груз Р=1 находится правее узла 8 (движение груза про­исходит по верхнему поясу фермы), удобнее рассматривать равно весие левой отсеченной части фермы (рис. 13,б), так как на нее в этом случае действует меньше сил, чем на правую.

Применяя для определения усилия U₇₉ способ моментнои точки, составим уравнение суммы моментов всех сил, действующих на левую часть фермы, относительно точки 6:

ΣM₆=R_A3d— U₇₉h=0, откуда

U₇₉=3R_Ad/h.

Таким образом, при положении груза Р= 1 на правой части фер­мы усилие U₇₉ равно левой опорной реакции R_A, Рис.13.

умноженной на постоянный коэффициент 3d / h. Одновременно

отмечаем, что 3R_Ad численно равно изгибающему моменту М°₆ в простой балке для сечения с абсциссой, равной абсциссе моментной точки 6.

Линия влияния усилия U₇₉ (когда груз Р=1 расположен правее узла 8) представляет собой линию влияния опорной реакции R_A с ординатами, умноженными на 3d / h. Поэтому для ее построения отложим на оси отсчета вверх на левой опорной вертикали орди­нату, равную 3d / h, и соединим прямой ее вершину с нулевой точкой на правой опорной вертикали; в результате получим прямую a₁b (рис. 13, г).

На построенную таким образом прямую, называемую правой прямой, сносим правые узлы фермы 8, 10, 12, 14 и 16. Заштриховы­ваем линию влияния на участке между узлами 8 и 16.

При грузе Р=1, расположенном левее узла 6, усилие в стержне 7—9 может быть найдено из уравнения равновесия для правой части фермы

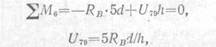
т. е. усилие в стержне 7—9 равно правой опорной реакции R_B, увеличенной в 5d/ h раз. Произведение 5R_Bd численно равно изги­бающему моменту М°₆ простой балки для сечения с абсциссой, рав­ной абсциссе моментнои точки 6.

Линия влияния U₇₉ для груза, расположенного левее узла 6, строится следующим образом: от оси отсчета вверх на правой опор­ной вертикали откладывается ордината, равная 5d/ h, после чего еевершина соединяется с нулевой точкой на левой опорной вертикали (прямая b₁ а на рис. 13, г). Построенная таким образом прямая носит название левой прямой; на эту прямую сносятся левые узлы фермы 1,2, 4 и 6. Заштриховываем линию влияния на участке между узлами 1 и 6.

Так как усилие U₇₉ определяется формулой

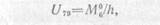
то его линия влияния может быть получена из линии влияния из­гибающего момента простой балки (для сечения, соответствующего вертикали, проходящей через моментную точку в ферме) умножением всех ее ординат на коэффициент 1/ h. Поэтому прямые b₁ а и a₁b (левая и правая), соединяющие вершины опорных ординат с нулевыми точками на противоположных опорах, пересекаются друг с другом под моментной точкой (в точке с). Передаточная прямая, (соответствующая движению груза Р=1 между узлами 6 и 8 рассе­ченной панели, в данном случае совпадает с продолжением правой прямой линии влияния.

Рассмотренный пример позволяет сформулировать порядок по­строения линий влияния усилий для элементов балочной фермы на двух опорах способом моментной точки:

1) при построении правой прямой следует отложить от оси отсчета на левой опорной вертикали (вверх или вниз, в зависимости от знака) ординату a/h, где а— расстояние от моментной точки до левой опорной вертикали, h — плечо определяемого усилия относительно моментной точки;

2) вершину опорной ординаты соединить с нулевой точкой на правой опорной вертикали;

3) на построенную таким образом правую прямую снести правые узлы фермы;

4) найти на правой прямой точку пересечения ее с левой пря­мой, для чего моментную точку снести на правую прямую;

5) точку пересечения правой и левой прямых соединить с нулевой точкой на левой опорной вертикали;

6) на построенную таким образом левую прямую снести левые узлы фермы;

7) вершины узловых ординат рассеченной панели соединить передаточной прямой.

Можно начинать построение линии влияния и с левой прямой. В этом случае на правой опорной вертикали откладывается от оси отсчета (вверх или вниз, в зависимости от знака) ордината b/h, где b — расстояние от моментной точки до правой опорной вертикали и h — плечо определяемого усилия относительно моментной точки. Затем через вершину отложенной таким образом ординаты и нулевую точку на левой опорной вертикали проводится левая прямая, после чего строятся правая и передаточная прямые.

Способ проекций.Построим линию влияния усилия в раскосе 6—9 фермы, изображенной на рис. 13, а.

Когда груз Р=1 расположен между узлами 8 и 16 (движение по верхнему поясу), рассматриваем равновесие левой отсеченной части фермы (рис. 13, б). Составим уравнение проекций всех сил на вертикальную ось:

ΣY=R _A— D₆₉ sin a=0, откуда

D₆₉=R_A/ sin a.

При грузе, расположенном между узлами 1 и 6, рассматриваем условие равновесия правой части фермы (рис. 13, в). Спроециро­вав все силы на вертикальную ось, получим

ΣY=R _В +D₆₉ sin а=0,

Откуда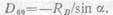

Формулы для усилия D₆₉ показывают, что пока груз расположен на правой части фермы, линия влияния D₆₉ может быть получена умножением ординат линии влияния опорной реакции R_A на по­стоянный коэффициент 1/sin а; когда же груз Р=1 находится в пре­делах левой части фермы, усилие D₆₉ равняется опорной реакции R_B, умноженной на (—1/sin а).

Для построения правой прямой откладываем от оси отсчета вверх на левой опорной вертикали ординату 1/sinа и соединяем ее вер­шину с нулевой точкой правой опорной вертикали (прямая a₁b на рис.13, д). На построенную таким образом правую прямую сно­сим правые узлы: 8, 10, 12, 14 и 16.

Для построения левой прямой от оси отсчета на правой опорной вертикали откладываем вниз ординату 1/sin а, вершину которой соединяем с нулевой точкой левой опорной вертикали. На построен­ную левую прямую (прямая ab₁ на рис. 13, д) сносим левые узлы: 1, 2, 4 и 6.

Передаточная прямая соединяет вершины узловых ординат рас­сеченной панели.

Заметим, что и в этом случае правая прямая пересекается с левой под моментной точкой. В самом деле, моментная точка для усилия D₆₉ находится в бесконечности; там же пересекаются правая и ле­вая прямые, параллельные между собой.

Линия влияния усилия D₆₉имеет участки с положительными и отрицательными ординатами. Следовательно, стержень 6—9 при движении груза по ферме может быть как сжат, так и растянут.

Построим теперь линию влияния усилия в стойке 6—7 (рис. 13, а). В этом случае способ моментной точки неприменим, так как приходится рассекать ферму сечением, в которое попадают четыре стержня (сечение //—// или ///—///).

Лучше всего здесь воспользоваться способом вырезания узлов (рис. 13, е). Вырезав узел 7, составим для него уравнение равнове­сия в виде суммы проекций всех сил на вертикальную ось:

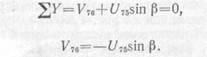
Так как груз Р= 1 к узлу 7 непосредственно не прикладывается (он движется по верху фермы), то полученная зависимость между усилиями V₇₆ и U₇₅ сохраняется при любом положении груза в пре­делах пролета фермы. Поэтому линия влияния V₇₆ может быть по­лучена из линии влияния U₇₅ умножением всех ее ординат на (-sin β).

Но усилие U₇₅ пока неизвестно; для определения его спроеци­руем силы, действующие на узел 7, на горизонтальную ось:

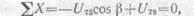
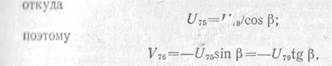
Этот результат можно получить и непосредственно из уравнения проекций сил, действующих на узел, на прямую, перпендикулярную элементу 7-5.

Таким образом, линия влияния V₇₆ может быть получена из построенной ранее способом моментной точки линии влияния U₇₉ умножением всех ее ординат на (—tg β). Построенная та­ким образом линия влияния V₇₆ изображена на рис. 13, ж.

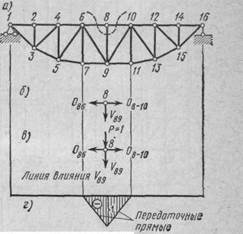Построим линию влияния для стойки 8—9 (рис. 14, а). Здесь так же, как и в преды­дущем случае, нельзя провес­ти разрез, пересекающий толь­ко три стержня. Поэтому вос­пользуемся способом выреза­ния узлов.

Вырезав верхний узел 8 (рис. 14, а) и рассмотрев его равновесие, получим:

1) при нагрузке в любом узле, кроме 8 (рис. 14, б),

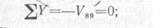
2) при нагрузке в узле 8 (рис. 14, в)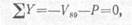

Откуда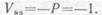

Следовательно, когда груз Р =1 приложен в узлах 1, 2, 4, 6 или 10, 12, 14, 16, усилие V₈₉=0; когда же груз Р = 1 приложен в узле 8, то V₈₉=—1. Найдя ординаты в узловых Рис.14.

точках и соединив вершины их прямыми, получим линию

влияния V₈₉ (рис. 14, г). Она имеет вид треугольника с наибольшей ординатой, равной еди­нице. Отрицательный ее знак указывает на то, что стойка 8—9 ра­ботает только на сжатие.

Вопросы для самопроверки:

1. Понятие фермы. Классификация ферм.

2. Определение усилий в стержнях простейших ферм методом моментной точки.

3. Сформулируйте порядок по­строения линий влияния усилий для элементов балочной фермы на двух опорах способом моментной точки.

4. Определение усилий в стержнях простейших ферм методом проекций

5. Построение линии влияния усилий в стержнях простейших ферм методом моментной точки.

6. Построение линии влияния усилий в стержнях простейших ферм методом проекций.