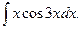Тема 2.4 Неопределенный интеграл
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу_ нахождение самой функции по ее производной или дифференциалу.
2.41 Первообразная функция и неопределенный интеграл .
Определение.Функция F(x) называется первообразной функцией для функции f(x) на промежутке Х, если в каждой точке х этого промежутка F/(x)=f(x).
Например, 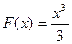 является первообразной для функции f(x)=x2, так как
является первообразной для функции f(x)=x2, так как 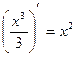 .
.

 y
y
 |
y =f(x)+c α
|



 F/(x)=tg α =f(x)
F/(x)=tg α =f(x)
 y=f(x) α
y=f(x) α
 C
C

0x x
Рис. 9
первообразную для f(x)- значит найти такую кривую y=F(x), что угловой коэффициент касательной к ней в произвольной точке х равен значению f(x) заданной функции в этой точке (см. рис.9).
следует отметить, что для заданной функции f(x) ее первообразная определена неоднозначно. Дифференцируя нетрудно убедиться, что функции 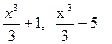 и вообще
и вообще 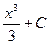 , где С –некоторое число, являются первообразными для функции f(x)=x2. Аналогично в общем случае, если F(x) – некоторая первообразная для f(x), то, поскольку (F(x)+C)/=F/(x) =f(x), функции вида F(x)+C, где С –произвольное число, также являются первообразными для f(x).
, где С –некоторое число, являются первообразными для функции f(x)=x2. Аналогично в общем случае, если F(x) – некоторая первообразная для f(x), то, поскольку (F(x)+C)/=F/(x) =f(x), функции вида F(x)+C, где С –произвольное число, также являются первообразными для f(x).
Геометрически это означает, если найдена одна кривая у=F(x), удовлетворяющая условию F/(x)=tg α=f(x), то сдвигая ее вдоль оси ординат, мы вновь получаем кривые, удовлетворяющие указанному условию *( поскольку такой сдвиг не меняет углового коэффициента касательной в точке с абсциссой х) (см.рис.9)
Основное свойство первообразной:
Если F(x) – первообразная для функции f(x) , то выражение вида F(x)+C, где С -произвольное число, задает всевозможные первообразные для функции для f(x).
Определение.Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интеграломот функции f(x) и обозначается 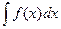 , где
, где 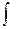 - знак интеграла, f(x)- подынтегральная функция , f(x)dx - подынтегральное выражение . Таким образом,
- знак интеграла, f(x)- подынтегральная функция , f(x)dx - подынтегральное выражение . Таким образом,
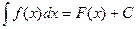 ,
,
где F(x) – некоторая первообразная для f(x), С- произвольная постоянная.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
2.42 Свойства неопределенного интеграла. Интегралы от основных элементарных функций.
Основные свойства неопределенного интеграла.
1. производная от неопределенного интеграла равна подынтегральной функции, т.е.
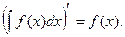
2.Постоянный множитель можно выносить за знак интеграла, т.е.
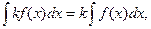
где k- некоторое число.
3.Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
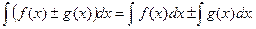
4.Пусть F(x) некоторая первообразная для функции f(x). Тогда
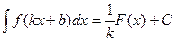 ,
,
где k и b–некоторые числа, k ≠0.
Таблица интегралов
| № п/п | функция | интеграл |
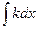 | kx+С | |
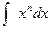 | 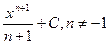 | |
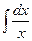 | ln|x|+C | |
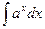 | 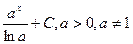 | |
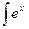 dx dx | ex+C | |
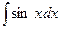 | -cos x+C | |
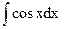 | sin x+C | |
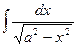 | arcsin 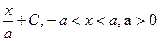 | |
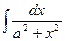 | 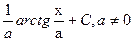 | |
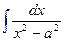 | 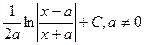 | |
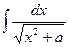 | 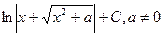 | |
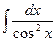 | tg x+C | |
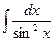 | -ctg x+C | |
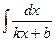 | 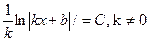 | |
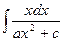 | 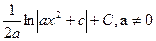 |
2.43 Методы интегрирования.
Существуют следующие методы интегрирования:
§ Интегрирование элементарных функций по таблице;
§ Метод замены переменной;
§ Метод интегрирования по частям;
Интегрирование по частям.
Пусть u(x) и v(x) – дифференцируемые функции. Метод интегрирования по частям основан на следующих равенствах:
(u.v)=u/.v+u.v/;
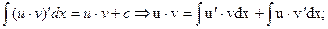
или
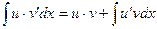 .
.
Например . Вычислить интегралы: а) 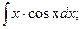 б)
б) 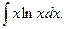
Решение:
а) Так как х/=1, а функция cosx при интегрировании обращается в
(-sinx), то данный интеграл можно найти интегрированием по частям, и полагая u(x) =x, v/(x) =cos x
u/(x)=1, v(x)= 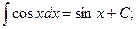
Подставляя, получаем:
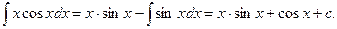
Ответ: 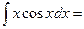
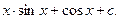
б) « Препятствием» к нахождению данного интеграла является присутствие сомножителя lnx в записи подынтегральной функции. Устранить его в данном случае можно интегрированием по частям, полагая u= lnx. Тогда dv=xdx.
Так как du=d lnx= 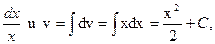 используем формулу интегрирования по частям; получаем
используем формулу интегрирования по частям; получаем
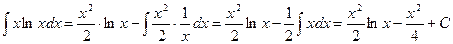
Ответ: 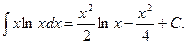
Анализируя разобранные примеры, можно указать следующие типы интегралов, для нахождения которых используется формула интегрирования по частям:
1. 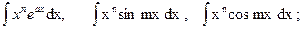
2. 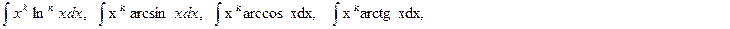
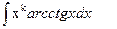
где a, m, k – действительные числа ( k≠-1), n- целое положительное число.
Для нахождения интегралов из первой группы формулу интегрирования по частям придется применять n раз (при первом применении полагают u= xn , а остальные сомножители подынтегрального выражения задают dv), пока степень n переменной х не станет равной нулю, а сам интеграл – табличным.
Для нахождения интегралов второй группы полагают xkdx=dv ( оставшиеся сомножители подынтегрального выражения задают тогда выражение для u). Отметим, что для нахождения 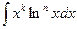 формулу интегрирования по частям придется применять n раз ( пи каждом применении степень функции ln x уменьшается на единицу, пока не станет равной нулю, а сам интеграл – табличным)
формулу интегрирования по частям придется применять n раз ( пи каждом применении степень функции ln x уменьшается на единицу, пока не станет равной нулю, а сам интеграл – табличным)
Интегрирование простейших рациональных дробей.
Рациональной дробью называют отношение двух многочленов. Например, 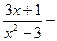 рациональная дробь.
рациональная дробь.
Рассмотрим общий подход к интегрированию рациональных дробей. Прежде всего, достаточно рассмотреть лишь правильные дроби, т.е. такие, у которых степень числителя меньше степени знаменателя. В самом деле, если это не так, то, используя алгоритм деления многочленов «углом», известный из школьного курса, мы можем представить исходную дробь в виде суммы многочлена и правильной дроби. Например,
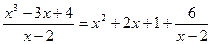 ,
,
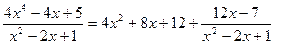
и т.д. Тогда интеграл от исходной дроби сведется к сумме интегралов от многочлена и правильной дроби.
Если степень знаменателя равна 1 , то искомый интеграл имеет вид 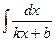 , и для его нахождения достаточно воспользоваться формулой (14).
, и для его нахождения достаточно воспользоваться формулой (14).
Пусть степень знаменателя равна 2, т.е. искомым является интеграл вида
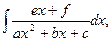
где a, b, c, e, f- действительные числа, а≠0.
При вычисления данного интеграла можно воспользоваться формулой (15) , для этого надо привести исходный интеграл к виду
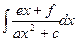 . Его можно привести к этому виду, если сначала выделить полный квадрат в знаменателе подынтегральной функции, а затем использовать соответствующую замену переменной.
. Его можно привести к этому виду, если сначала выделить полный квадрат в знаменателе подынтегральной функции, а затем использовать соответствующую замену переменной.
Пример. Найти интегралы:
а) 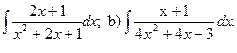
Решение:
а) Поскольку х2+2х+1=(х+1)2, то используем замену переменной
t= x+1. Тогда dt=dx, x=t-1 u

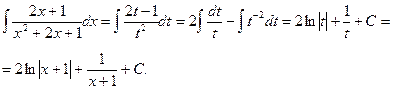
Ответ: 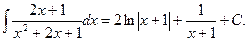
b) Так как 4х2+4х-3=(2х+1)2-4, то положим t= 2x+1. Тогда 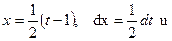

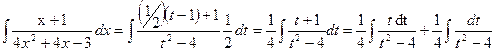
При нахождении первого интеграла воспользуемся формулой (15) при а=1, с=-4. второй интеграл – (10). Теперь имеем
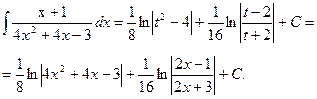
Ответ : 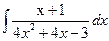
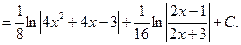
Упражнения:
- Вычислить неопределенный интеграл:
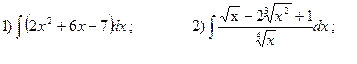



 2.
2.
2. Проинтегрировать функции:
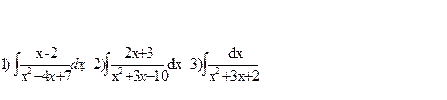
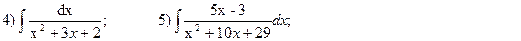
3.Проинтегрировать по частям
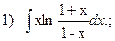 2)
2) 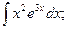 3)
3) 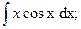 4)
4) 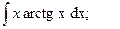
5)