Допускающие понижение порядка

Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть этого метода состоит в том, что с помощью замены переменной (подстановки) данное ДУ сводится к уравнению, порядок которого ниже.

Рассмотрим три типа ДУ, допускающих понижение порядка.

I тип: ДУ вида .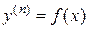

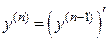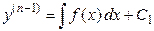Так как , то , где 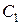- постоянная интегрирования.

Интегрируя еще раз, получаем

.

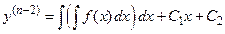Продолжая далее, получим, наконец (после 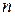интегрирований), выражение общего решения. Чтобы найти частное решение, при заданных начальных условиях находим значения произвольных постоянных.

Пример 2.1. Найти частное решение ДУ

,

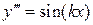удовлетворяющее начальным условиям

, , .

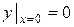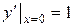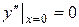Решение. Сначала находим :

.

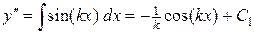Далее

.

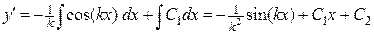И, наконец,

.

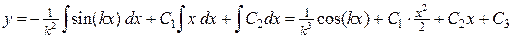Итак, общее решение имеет вид

.

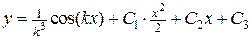Учитывая начальные условия, находим постоянные 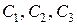. Получаем следующую систему уравнений:

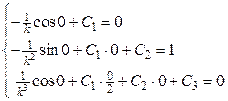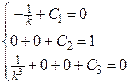Þ Þ .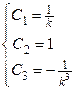

Следовательно, получаем следующее частное решение

.

,

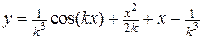II тип: ДУ вида ,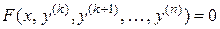

не содержащие искомой функции и ее производных .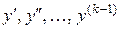

Данное уравнение с помощью замены 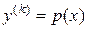можно свести к уравнению 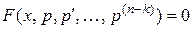порядка 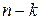. Предположим, что для полученного уравнения найдено общее решение 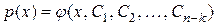. Тогда искомую функцию 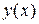можно получить путем 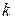-кратного интегрирования функции .

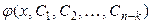Простейшее из таких уравнений имеет вид 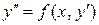. С помощью подстановки 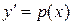его сводим к уравнению первого порядка 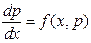с неизвестной функцией 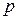, а затем из уравнения 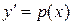находим .

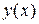Пример 2.2. Найти частное решение ДУ

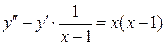при .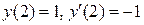

Решение. Это уравнение вида 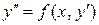. Полагая 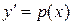, , 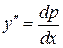получаем линейное ДУ первого порядка относительно неизвестной функции :

.

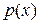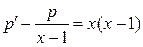Полагая в последнем уравнении 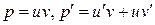, получаем:

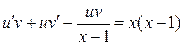или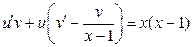

Далее решая, получаем сначала 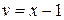, а потом .

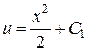Следовательно,

.

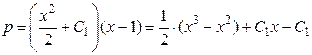Возвращаясь к 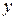, получаем:

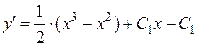
Тогда

.

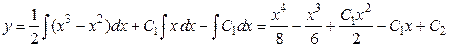Таким образом, общее решение исходного уравнения имеет вид:

.

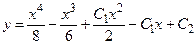Воспользовавшись начальными условиями, получаем систему:

.

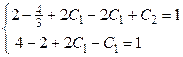Откуда 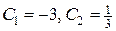. Следовательно, частное решение исходного уравнения имеет вид:

.

,

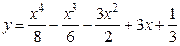III тип: ДУ вида ,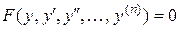

Не содержащие независимой переменной.

Если положить 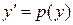, а за новую переменную принять 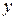, то порядок данного уравнения понизится на единицу. В этом случае производные 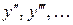находят по правилу дифференцирования сложной функции:

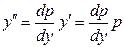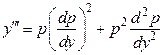, , и т.д.

Простейшее из таких уравнений имеет вид 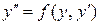. С помощью подстановки 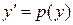его сводят к уравнению 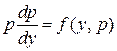с неизвестной функцией 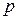, затем из уравнения 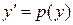находят .

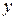Линейные дифференциальные уравнения

Высших порядков

Определение 2.3. Линейным ДУ 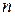-го порядка называется уравнение вида

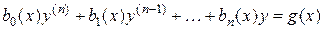, (2.1)

где 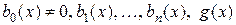- заданные функции от .

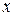Оно содержит искомую функцию 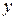и все ее производные лишь в первой степени. Функции 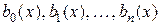называются коэффициентами уравнения (2.1), а функция 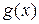- ее свободным членом (правой частью).

Если свободный член 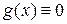, то уравнение (2.1) называется линейным однородным уравнением; если 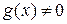, то уравнение (2.1) называется неоднородным.

Разделив уравнение (2.1) на 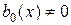и обозначив

,

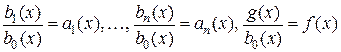получаем уравнение в виде приведенного:

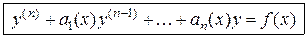. (2.2)

В уравнении (2.2) коэффициенты и свободный член считаются непрерывными функциями.

Установим некоторые свойства (примем без доказательства) линейных однородных уравнений, ограничившись уравнением второго порядка.

Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка, которое имеет следующий вид:

.

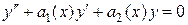Теорема 2.2.Если функци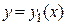и и 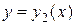- два частных решения ЛОДУ второго порядка, то функция 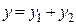также является решением этого уравнения.

Теорема 2.3.Если функция 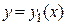- есть частное решение ЛОДУ второго порядка, то функция 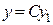также является решением этого уравнения.

Далее введем понятия линейно независимые и линейно зависимые решения ЛОДУ второго порядка.

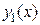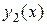Определение 2.4. Два решения ЛОДУ второго порядка и называются линейно независимыми на промежутке 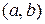, если их отношение на этом промежутке не является постоянным, т.е.

.

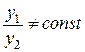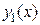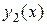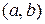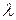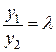Два решения и называются линейно зависимыми на промежутке , если существует такое постоянное число , что при 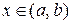. В этом случае .

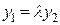Например, пусть имеем уравнение 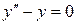. Легко проверить, что функции 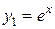, , 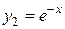, 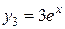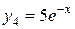являются решениями этого уравнения. При этом функци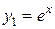и и 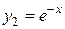линейно независимы на любом отрезке, так как отношение 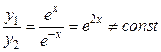. Функци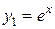и и 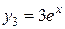являются линейно зависимыми, так как .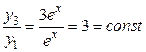