Задача 2 (радиоактивный распад)
Основные понятия
Дифференциальных уравнений
При решении различных задач математики, физики, химии, экономики и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную, искомую функцию и ее производную. Такие уравнения называются дифференциальными (термин принадлежит Г. Лейбницу, 1676 г.). Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Так, решением уравнения 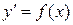 является функция
является функция 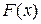 - первообразная для функции
- первообразная для функции 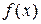 .
.
Задачи, приводящие к дифференциальным уравнениям
Рассмотрим две физические задачи, решение которых приводит к дифференциальным уравнениям. Но заметим, что при решении задач физического характера, приводящих к дифференциальным уравнениям, основную трудность представляет, как правило, составление самих дифференциальных уравнений. Здесь нет общего метода, и каждая задача требует своего подхода, основанного на знании соответствующего закона физики.
Задача 1 (движение материальной точки).
Материальная точка массы 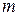 замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости
замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости 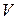 . Найти зависимость скорости от времени.
. Найти зависимость скорости от времени.
Решение. Примем за независимую переменную время 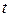 , отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки
, отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки 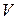 будет функцией
будет функцией 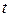 , т.е.
, т.е. 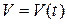 . Для нахождения
. Для нахождения 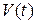 воспользуемся вторым законом Ньютона (основным законом механики):
воспользуемся вторым законом Ньютона (основным законом механики): 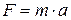 , где
, где 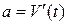 - есть ускорение движущегося тела,
- есть ускорение движущегося тела, 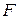 - результирующая сила, действующая на тело в процессе движения.
- результирующая сила, действующая на тело в процессе движения.
В данном случае 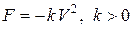 - коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция
- коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция 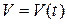 является решением дифференциального уравнения
является решением дифференциального уравнения
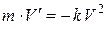 или
или 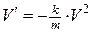 , где
, где 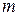 - масса тела.
- масса тела.
Это же уравнение можно записать так
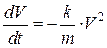 .
.
,
Задача 2 (радиоактивный распад).
Экспериментальным путем установлено, что скорость радиоактивного распада пропорциональна количеству нераспавшегося вещества. Считая, что начальное количество вещества 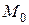 , найти зависимость между количеством нераспавшегося вещества
, найти зависимость между количеством нераспавшегося вещества 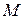 и временем
и временем 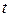 .
.
Решение. Скорость радиоактивного распада равна производной от количества вещества 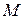 по времени
по времени 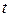 , т.е.
, т.е. 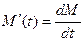 . Учитывая условие, получаем следующее дифференциальное уравнение
. Учитывая условие, получаем следующее дифференциальное уравнение
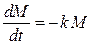 ,
,
где 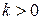 - коэффициент пропорциональности.
- коэффициент пропорциональности.
Знак минус берется потому, что с возрастанием 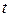 количество вещества
количество вещества 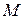 уменьшается, а значит, производная не положительна.
уменьшается, а значит, производная не положительна.
Можно убедиться, что частным решением данного уравнения является функция
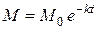 .
.
,
Определение 1.1. Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную 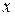 , искомую функцию
, искомую функцию 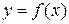 и ее производные
и ее производные 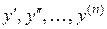 . ДУ записывается так:
. ДУ записывается так:
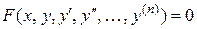
или
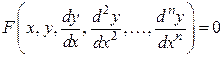 .
.
Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называется обыкновенным, в противном случае – ДУ в частных производных.
Определение 1.2. Порядком ДУ называется порядок наивысшей производной, входящей в уравнение.
Например, уравнение 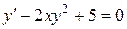 - обыкновенное ДУ первого порядка; уравнение
- обыкновенное ДУ первого порядка; уравнение 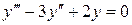 - ДУ третьего порядка;
- ДУ третьего порядка; 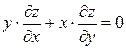 - ДУ в частных производных первого порядка.
- ДУ в частных производных первого порядка.
Определение 1.3. Решением ДУ называется функция, которая при подстановке ее вместе с производной в это уравнение превращает его в тождество.
Например, для уравнения 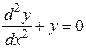 функции вида
функции вида 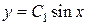 ,
, 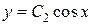 или
или 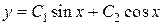 , где
, где 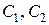 - любые постоянные, являются решениями данного уравнения. Например, для уравнения
- любые постоянные, являются решениями данного уравнения. Например, для уравнения 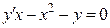 функция вида
функция вида 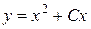 , где
, где 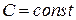 , является решением данного уравнения.
, является решением данного уравнения.
Основные понятия
