Основные теоретические положения. Плоскость в пространстве однозначно определена тремя точками

Плоскость в пространстве однозначно определена тремя точками, не лежащими на одной прямой. В связи с этим существует несколько способов задания плоскости на эпюре, среди которых отметим следующие (рис.5.1):

1) тремя точками, не принадлежащими одной прямой (рис.5.1,а);

2) любой плоской фигурой, например, треугольником (рис.5.1,б);

3) прямой, и не принадлежащей ей точкой (рис.5.1,в);

4) двумя пересекающимися прямыми (рис.5.1,г);

5) двумя параллельными прямыми (рис.5.1,д).

Виды плоскостей. Плоскость, произвольно расположенная в пространстве (по отношению к плоскостям проекций), называется плоскостью общего положения. Все плоскости, изображенные на рис.5.1 являются плоскостями общего положения.

Плоскость, перпендикулярная одной или двум плоскостям проекций, называется плоскостью частного положения, причем плоскость перпендикулярная одной из плоскостей проекций носит название проецирующей плоскости: горизонтально проецирующей если a^p₁ или фронтально-проецирующей a^p₂ (рис.5.2). На эпюрах проецирующие плоскости задаются своим следом на соответствующей плоскости проекций.

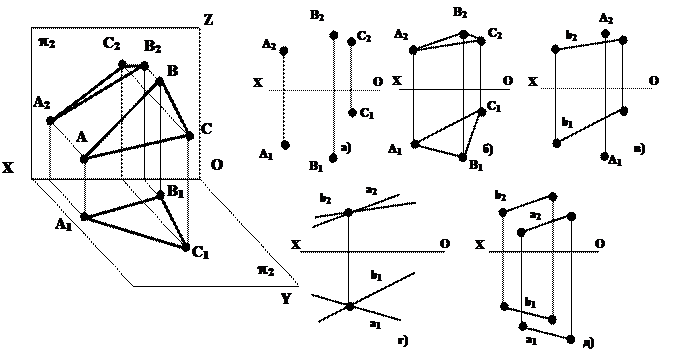
Рис.5.1

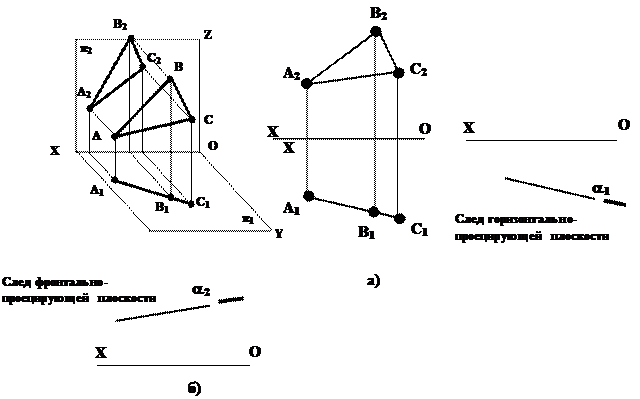
Рис.5.2

Прямая принадлежит плоскости, если:

а) имеет, по крайней мере, две общие с плоскостью точки (прямая b, рис.5.3) ;

б) когда она имеет одну общую точку и параллельна какой-либо прямой в этой плоскости (прямая aêê(BC), рис.5.3).

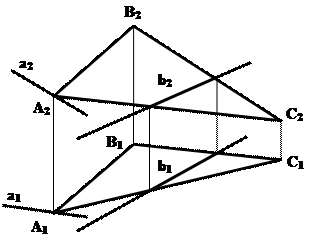
Рис.5.3

Через любую точку плоскости можно провести главные линии плоскости – фронталь и горизонталь, прямые, лежащие в плоскости и параллельные либо p₁ либо p₂ соответственно. Таких линий в плоскости можно провести сколько угодно.

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости.

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой. Если параллельны две проецирующие плоскости, то на эпюре параллельны из одноименные следы.

Две плоскости пересекаются по прямой линии. Для построения линии пересечения двух плоскостей достаточно построить две точки, принадлежащей одновременно двум заданным плоскостям. Для построения линии пересечения двух плоскостей общего положения обычно используют метод вспомогательных секущих плоскостей.

Примеры решения задач

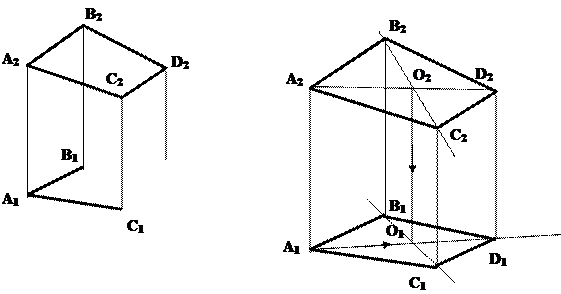
Задача 1. Достроить плоский четырехугольник (рис.5.4).

Дано: Решение:

Рис.5.4

Решение задачи сводится к построению недостающей проекции точки D, принадлежащей плоскости, заданной точками А,В,C. Зададим эту плоскость треугольником АВC, для чего соединим точки В и C прямой линией на обеих проекциях. Проведем фронтальную проекцию диагонали четырехугольника А₂D₂. Затем достроим вторую ее проекцию, для чего из точки пересечения фронтальных проекций диагоналей (точка О₂) опустим линию проекционной связи на прямую D₁C₁. Прямая А₁О₁ задаст направление диагонали четырехугольника на горизонтальной проекции. Пересекаем Прямую А₁О₁ с соответствующей линией связи (из D₂), получаем искомую проекцию точки С. Точка С принадлежит плоскости треугольника АВС, т.к. принадлежит прямой АО, лежащей в этой плоскости. Прямая принадлежит плоскости треугольника АВС, т.к. имеет с ней две общие точки (А и О). Следовательно, достроенный четырехугольник – плоский.

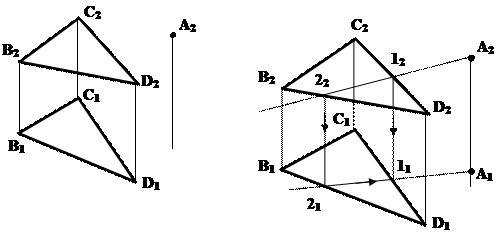Задача 2. Достроить точку А, если она принадлежит плоскости D ВСD (рис.5.5). Дано: Решение:

Рис.5.5

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости. Через известную проекцию точки А - точку А₁- проводим произвольную прямую. Строим вторую проекцию введенной прямой, которая должна лежать в заданной плоскости. Для этого фиксируем точки пересечения 1₂ и 2₂ со сторонами треугольника В₂D₂ и C₂D₂. Отыскиваем горизонтальные проекции точек 1 и 2 на соответствующих сторонах горизонтальной проекции треугольника ВСD. Строим горизонтальную проекцию прямой 12 (1₁2₁), пересечение которой с линией связи из точки А₂, определит искомую проекцию точки А.

Задача 3. Через заданную точку Е с помощью главных линий построить плоскость b(hÇf) параллельно заданной плоскости a(a||b). Построенную плоскость задать параллельными прямыми (рис.5.6).

Дано:

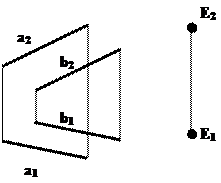
Решение:

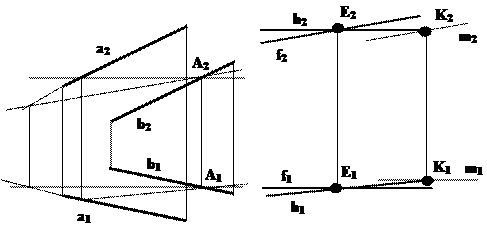
Рис.5.6

Построим вначале главные линии плоскости a. Построение главных линий начинают с проведения тех проекции, направление которых всегда известно (у горизонтали - это ее фронтальная проекция h'₂||OX ; у фронтали - ее горизонтальная проекция f''₁||OX ). На рис. 5.6 главные линии плоскости проведены через точку А, произвольно выбранной в плоскости a. Проведя затем через точку E параллельные прямые (h'₂||h₂ и f''₁|| f'₁), най­дем искомую плоскость b(hÇf) || a(a||b). Для того, чтобы перезадать плоскость b(hÇf) параллельными прямыми, достаточно через любую точку плоскости, например, через выбранную произвольно точку К, провести прямую m, параллельно любой прямой, лежащей в этой плоскости (в данном примере m||f, при этом m₁||f₁ и m₂||f₂). Плоскость b теперь задана параллельными прямыми m||f.

Задача 4. Построить линию пересечения двух плоскостей: плоскости общего положения a(aÇb) и фронтально-проецирующей плоскости b(b₂)(рис.5.7).

Дано: Решение:

Рис.5.7

Линия пересече­ния двух плоскостей в данном случае определяется двумя точками пересече­ния следа фронтально-проецирующей плоскости b₂ с двумя прямыми а и с в пло­скости a. При этом прямая с(с₁,с₂) - дополнительная, проведенная произ­вольно в плоскости, но так, чтобы точка К линии пересече­ния получилась в поле заданного чертежа. Точки К и L являются общими для двух заданный плоскостей, а , следовательно, и определяют искомую линию пересечения: (КL)= a(aÇb) Ç b(b₂).

Задача 5. Построить линию пересечения двух плоскостей общего положения: a(DАВС) и b(а||b)(рис.5.8).

Дано:

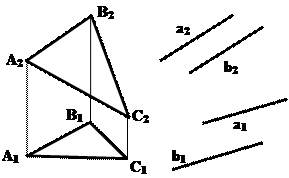
Решение:

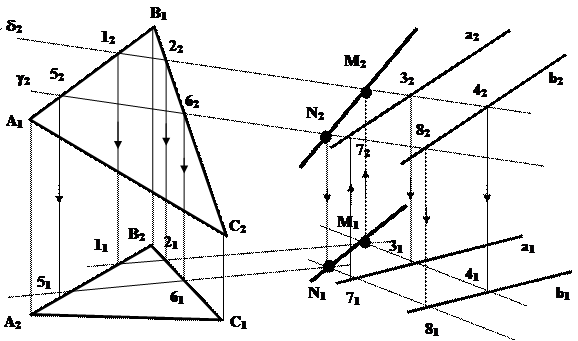
Рис. 5.8

При решении этой задачи используется метод секущих плоскостей. Так как две плоскости пересекаются по прямой линии, определяемой двумя точками, для построения необходимо ввести две дополнительные секущие плоскости. Порядок решения задачи:

1. Вводим дополнительную секущую плоскость d( d₂). В качестве секущей плоскости выбрана фронтально-проецирующая плоскость, заданная своим следом на фронтальной плоскости проекций. (В качестве секущей плоскости может быть выбрана произвольная проецирующая плоскость).

2. Строим линию пересечения фронтально-проецирующей плоскости d(d₂) с плоскостью общего положения a(DАВС) (см.пример 4): 12(1₁2₁;1₂2₁)= d( d₂) Ça(DАВС).

3. Строим линию пересечения фронтально-проецирующей плоскости d(d₂) с плоскостью общего положения b(а||b): 34(3₁4₁;3₂4₂)= d( d₂) Çb(а||b).

4. Строим точку М как точку пересечения прямых 12 и 34: М₁=1₁2₁ Ç3₁4₁ Вторая проекция точки М точка М₂, отыскивается на следе вспомогательной секущей плоскости d( d₂) с помощью лини проекционной связи. Точка М является искомой точкой, поскольку принадлежит одновременно трем плоскостям: вспомогательной d( d₂) и заданных a(DАВС) и b(а||b), и , следовательно, является точкой, принадлежащей линии пересечения двух исходных плоскостей.

5. Аналогично строится вторая точка, принадлежащая линии пересечения N. Для этого вводится еще одна вспомогательная секущая плоскость g(g₂). Плоскость g(g₂) также является фронтально-проецирующей плоскостью, кроме того, параллельной плоскости d( d₂). Это является необязательным, поскольку вспомогательные плоскости могут быть выбраны совершенно произвольно.

6. После построения точки N проводим прямую MN, которая является искомой линией пересечения двух исходных плоскостей.

Задача 6. Построить линию пересечения двух плоскостей общего положения a(DАВС) и b(DDEF) (рис.5.9).

Дано:

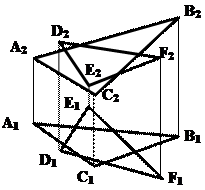Рис.5.9

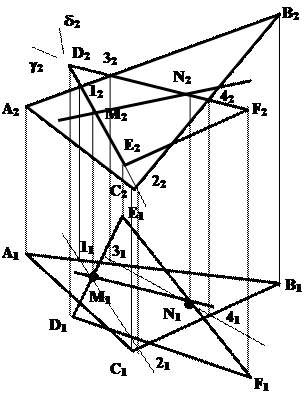Решение:

Рис. 5.9 (продолжение)

Задача решается аналогично предыдущей. Для уменьшения количества вспомогательных построений в качестве секущих введены плоскости d( d₂) и g(g₂) через прямые, принадлежащие одной из плоскостей (DE и DF), следы секущий плоскостей совпадают соответствующими проекциями этих прямых.