Алгоритм ближайшего соседа

Глава 4. Графы

Введение в теорию графов

Настоящая глава посвящена теории графов. Теория графов применяется в таких областях, как физика, химия, теория связи, проектирование ЭВМ, электротехника, машиностроение, архитектура и т. д. Эта теория тесно связана со многими разделами математики, среди которых теория групп, теория матриц, численный анализ, теория вероятностей, топология и комбинаторный анализ. На графах рассматриваются важные практические проблемы, многие из которых требовали тонких математических методов. Уже в середине XIX века Киргхоф применил графы для анализа математических цепей, а Кэли исследовал важный класс графов для выявления и перечисления изомеров насыщенных углеводородов (1857г.). Однако теория графов как математическая дисциплина сформировалась только в середине 30-х годов XX века благодаря работам таких математиков, как Кениг Г., Понтрягин Л.С., Зыков А.А., Визинг В.Г., и другие.

Впервые понятие «граф» ввел в 1936 году венгерский математик Денни Кениг. Но первая работа по теории графов принадлежит Леонарду Эйлеру и была написана еще в в 1736 году. Известный математик Леонард Эйлер, пытался решить теперь уже классическую задачу о Кенигсбергских мостах. В то время в городе Кенигсберге было два острова, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рис. 1.1. Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер изобразил Кенигсберг в виде графа, отождествив его вершины с частями города, а ребра — с мостами, которыми связаны эти части. Как мы покажем, Эйлеру удалось доказать, что искомого маршрута обхода города не существует.

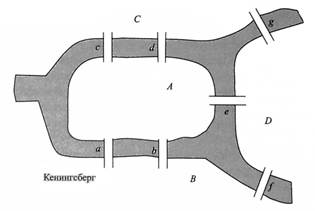
Рис.4. 1. Схема старого Кенигсберга

Графы и терминология

На рис. 4.1 изображены семь мостов Кенигсберга так, как они были расположены в восемнадцатом столетии. В задаче, к которой обратился Эйлер, спрашивается: можно ли найти маршрут прогулки, который проходит ровно один раз по каждому из мостов и начинается и заканчивается в одном и том же месте города?

Модель задачи — это граф, состоящий из множества вершин и множества ребер, соединяющих вершины. Вершины А, В, С и D символизируют берега реки и острова, а ребра а, b, с, d, e, f и g обозначают семь мостов (см. рис. 4.2). Искомый маршрут (если он существует) соответствует обходу ребер графа таким образом, что каждое из них проходится только один раз. Проход ребра, очевидно, соответствует пересечению реки по мосту.

Граф, в котором найдется маршрут, начинающийся и заканчивающийся в одной вершине, и проходящий по всем ребрам графа ровно один раз, называется эйлеровым графом. Последовательность вершин (может быть и с повторениями), через которые проходит искомый маршрут, как и сам маршрут, называется эйлеровым циклом. Эйлер заметил, что если в графе есть эйлеров цикл, то для каждого ребра, ведущего в какую-то вершину, должно найтись другое ребро, выходящее из этой вершины, и получил из этого простого наблюдения такой вывод: если в данном графе существует эйлеров цикл, то к каждой вершине должно подходить четное число ребер.

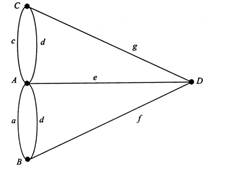
Рис.4.2. Модель задачи о мостах Кенигсберга.

Кроме того, Эйлеру удалось доказать и противоположное утверждение, так что граф, в котором любая пара вершин связана некоторой последовательностью ребер, является Эйлеровым тогда и только тогда, когда все его вершины имеют четную степень. Степенью вершины v называется число S(v) ребер из нее выходящих (ей инцидентных). Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной.

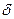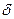Теперь совершенно очевидно, что в графе, моделирующем задачу о мостах Кенигсберга, эйлерова цикла найти нельзя. Действительно, степени всех его вершин нечетны: (В) = (С) — 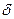(D) = 3 и 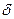(А) = 5. С легкой руки Эйлера графы, подобные тому, который мы исследовали при решении задачи о мостах, стали использоваться при решении многих практических задач, а их изучение выросло в значительную область математики.

Простой граф определяется как пара G = (V, Е), где V — конечное множество вершин, а Е — конечное множество ребер, причем G не может содержать петель (ребер, начинающихся и заканчивающихся в одной вершине) и кратных ребер (кратными называются несколько ребер, соединяющих одну и ту же пару вершин). Естественно, что множество ребер графа не может быть пустым, в то время как множество ребер (дуг) может быть пустым.

Граф, изображенный на рис. 1, не является простым, поскольку, например, вершины А и В соединяются двумя ребрами (как раз эти ребра и называются кратными).

Графы бывают двух видов – ориентированные и неориентированные. Ориентированным графом (орграфом) называется тройка G = (V, Е,f), где V – множество вершин графа, Е – множество дуг, а ,f – отображение 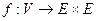, называемое отображением инцидентности.

В орграфе каждому ребру (дуге) 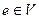однозначно отвечает упорядоченная пара точек (вершин) 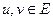, в то время, как в неориентированном графе порядок перечисления вершин роли не играет.

Ребро е соединяет вершины и и v, а вершины при этом называются концевыми. Ребра, имеющие одинаковые концевые вершины и сами одинаково направленные, называются параллельными (кратными); противоположно направленные ребра – противоположными. Вершина и ребро называют инцидентными друг другу, если вершина является для этого ребра концевой точкой. Две вершины и и v в простом графе называются смежными, если они соединяются каким-то ребром е, про которое говорят, что оно инцидентно вершине и (и v).

Таким образом, мы можем представлять себе множество Е ребер как множество пар смежных вершин, определяя тем самым нерефлексивное, симметричное отношение на множестве V. Рефлексивность отношения, в данном случае, обозначает то, что в простом графе нет петель, т. е. ребер, оба конца которых находятся в одной вершине. Симметричность отношения вытекает из того факта, что ребро е, соединяющее вершину и с v, соединяет и v c и (иначе говоря, ребра не ориентированы, т. е. не имеют направления). Единственное ребро простого графа, соединяющее пару вершин и и v, мы будем обозначать как uv (или vu).

Логическая матрица отношения на множестве вершин графа, которое задается его ребрами, называется матрицей смежности. Матрица смежности заполняется символами «И» или «Л» (или «1» или «0») в зависимости от того, соединены или нет вершины в графе. Симметричность отношения в терминах матрицы смежности М означает, что матрица М симметрична относительно главной диагонали. Рефлексивность отношения в терминах матрицы смежности означает наличие на главной диагонали символа «И» (или «1»). А нерефлексивность этого отношения означает наличие на главной диагонали матрицы М стоит символа «Л» (или «0»).

Пример 1. Нарисуйте граф G(V,E) с множеством вершин V={a,b,c,d,e} и множеством ребер E={ab, ae, bc, bd, ce, de}. Выпишите его матрицу смежности.

Решение. Граф G показан на рис.4.3..

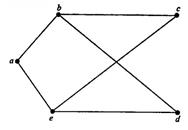
Рис. 4.3.

Его матрица смежности имеет вид:

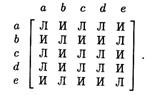
Для восстановления графа нам достаточно только тех элементов матрицы смежности, которые стоят над главной диагональю.

Путем в графе называется такая последовательность ребер, ведущая от некоторой начальной вершины u в некоторую вершину v, в которой каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза.

Пример 2. На рис.4.4 произвольный ориентированный граф задан своей диаграммой. Проиллюстрировать на этом графе введенные выше понятия.

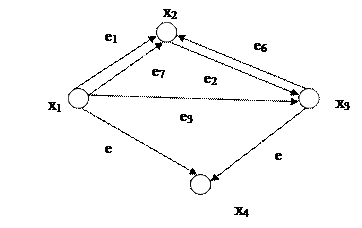Рис.4.4.

Решение. Граф G = (V, Е,f) имеет множество вершин 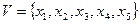множество дуг 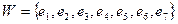, при этом ; ; ; ; ; .

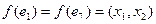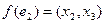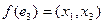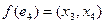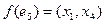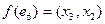Ребра 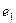и 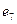– параллельные ребра;

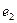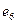ребра и – противоположные ребра;

ребро 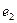как и ребро 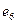инцидентно вершинам 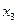и ;

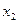ребро 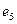инцидентно вершинам 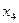и 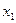; и т. д.

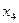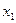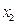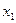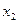Вершины и 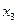, 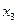и , и 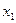, 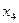и , и 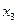– являются смежными.

Пары ребер 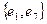, , 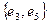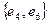и т.д. так же являются смежными.

Степень вершин 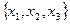равна 4, степень вершины 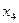равна 2, степень вершины 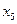равна 0 – она является изолированной.

Последовательность ребер 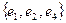, , 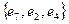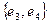и 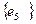образуют пути, ведущие из вершины 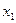в вершину .

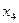Путь для неориентированных графов называется маршрутом. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей.

В любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно. В орграфе различают положительные и отрицательные степени вершин, которые равны числу исходящих из вершины ребер и заходящих в вершину ребер. Суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны также числу всех дуг.

Граф без петель и кратных ребер называют простым графом. Граф без петель, но с кратными ребрами называют мультиграфом. Наиболее общий случай графа, когда допускаются петли и кратные ребра, называют псевдографом. Граф без ребер называют нуль-графом. Простой граф, в котором любые две вершины соединены ребром, называется полным. Если множество вершин V простого графа допускает разбиение на два непересекающихся подмножества 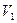и 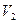, ( 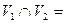Ø) так, что не существует ребер, соединяющих вершины одного и того же подмножества, то граф называется двудольным или биграфом (рис. 4.5.)

Рис. 4.5. Пример двудольного графа

Маршрутом длины k в графе G называется такая последовательность вершин v₀,v₁,…,v_k, что для каждого i= 1,...,k пара v_i-1v_i образует ребро графа. Мы будем обозначать такой маршрут через v₀ v₁…v_k.

Маршрут, все ребра которого различны, называется цепью. Маршрут, у которого различны все вершины, называется простой цепью. Замкнутая цепь называется циклом, а замкнутая простая цепь – простым циклом.

Или циклом в графе принято называть последовательность вершин v₀,v₁,…,v_k, каждая пара которых является концами одного ребра, причем v₀=v₁, а остальные вершины (и ребра) не повторяются. Иными словами, цикл — это замкнутый маршрут, проходящий через каждую свою вершину и ребро только один раз.

Граф, в котором нет циклов, называется ацикличным. Структуры деревьев, которые возникают в вычислениях, представляют собой частный случай ацикличных графов.

Пример 3. Пример цепей и циклов в псевдографе приведен на рис.4. 6.

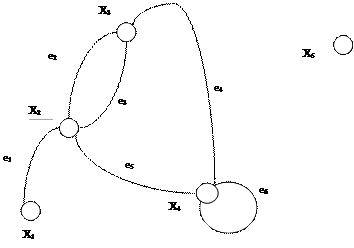Рис. 4.6.

Пример цепей и циклов в псевдографе: 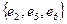– цепь; 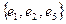– простая цепь; 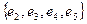– цикл; 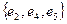– простой цикл.

Для ориентированных графов все введенные понятия сохраняются с заменой терминов маршрутов на путь, а цикла на контур.

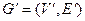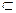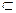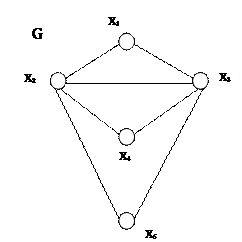
Граф называется частью графа G = (V, Е), если Е' Е и V’ V. Часть графа, которая наряду с некоторым подмножеством ребер содержит и все инцидентные им вершины, называется подграфом. Часть графа, которая наряду с некоторым подмножеством ребер содержит все вершины графа (Е' 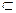Е и V’ = V), называется суграфом. Примеры разных частей графа приведены на рис. 4.7.

а) б)

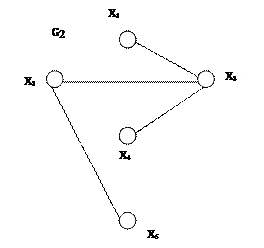
в) г)

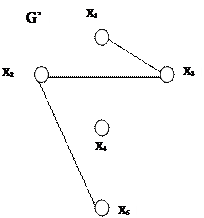
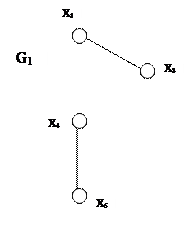
Рис. 4.7. Примеры различных частей графа G: а) неориентированный граф G; б) G’ – часть графа G; в) G₁ – подграф G; г) G₂ – суграф G.

Граф называют связным, если любую пару его вершин соединяет какой-нибудь маршрут. Любой общий граф можно разбить на подграфы, каждый из которых окажется связным. Минимальное число таких связных компонент называется числом связности графа и обозначается через c(G). Вопросы связности имеют важное значение в приложениях теории графов к компьютерным сетям. Следующий алгоритм применяется для определения числа связности графа.

Пример 4.Проследите за связностью на графе, изображенном на рис. 4.8.

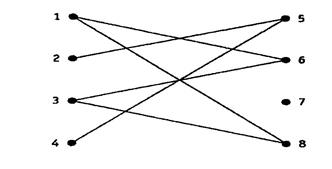Рис4.8.

Решение. Смотри табл. 4.1.

Таблица 4.1.

	V’ с
Исходные значения Выбор у = 1 Выбор у = 2 Выбор у = 7	{1, 2, 3, 4, 5, 6, 7, 8} 1 {1,3,6,8} 2 {2, 4, 5} 3 {7}

Итак, c(G) = 3. Соответствующие компоненты связности приведены на рис. 4.9.

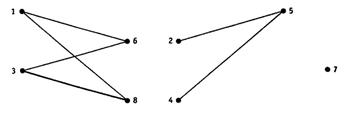
Рис. 4.9.

Гамильтоновы графы

Мы начали эту главу сизучения эйлеровых графов, обладающих замкнутым маршрутом, который проходит по всем ребрам графа ровно один раз. Похожая задача состоит в поиске цикла, проходящего через каждую вершину графа в точности один раз. Такой цикл, если он существует, называется гамильтоновым, а соответствующий граф — гамильтоновым графом.

Гамильтоновы графы служат моделью при составлении расписания движения поездов, для телекоммуникационных сетей, и т. д. В отличие от задачи Эйлера, простого критерия гамильтоновости графа пока не известно. Поиск хорошего критерия остается одной из главных нерешенных задач теории графов.

Тем не менее, многие графы являются гамильтоновыми. Предположим, что в каком-то графе любая пара вершин соединена ребром. Такой граф называется полным и обозначается через К_n, где п - число его вершин. Очевидно, в любом полном графе можно отыскать гамильтонов цикл.

Полный граф К₅ изображен на рис. 4.10. Его цикл a b с d e a очевидно, является гамильтоновым. В нем есть и другие гамильтоновы циклы. Поскольку каждая вершина смежна с остальными, то начиная с вершины а, в качестве второй вершины цикла мы можем выбрать любую из четырех оставшихся. Далее у нас будет три варианта для выбора третей вершины и два для четвертой, после чего мы вернемся в вершину а. Таким образом, у нас есть 4 *3 *2 = 24 цикла. Поскольку каждый цикл можно проходить как в одном направлении, так и в другом, то реально в графе К₅ есть только 12 разных гамильтоновых циклов.

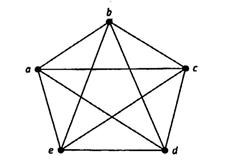
Рис. 4.10. Полный граф K₅

Поиск гамильтонова цикла (если он существует) в произвольном (связном) графе – задача далеко не всегда простая. Ответ на вопрос о гамильтоновости графа может оказаться довольно трудоемким.

Пример 5.Покажите, что граф, изображенный на рис. 4.11, не является гамильтоновым.

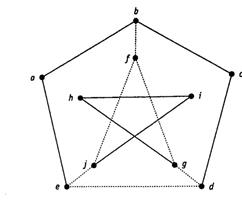
Рис. 4.11. Пример не гамильтонова графа

Решение.Предположим, что в связном графе найдется гамильтонов цикл. Каждая вершина v включается в гамильтонов цикл С выбором двух инцидентных с ней ребер, а значит, степень каждой вершины в гамильтоновом цикле (после удаления лишних ребер) равна 2. Степени вершин данного графа — 2 или 3. Вершины степени 2 входят в цикл вместе с обоими инцидентными с ними ребрами. Следовательно, ребра ab, ae, cd, cb, hi, hg иij в том или ином порядке входят в гамильтонов цикл С (см. рис. 4. 11).

Ребро bf не может быть частью циклаС, поскольку каждая вершина такого цикла должна иметь степень 2. Значит, ребра fi и fg обязаны входить в цикл С, чтобы включить в него вершину f. Но тогда ребра je и gd никак не могут принадлежать циклу С, поскольку в противном случае в нем появятся вершины степени три. Это вынуждает нас включить в цикл ребро ed, что приводит нас к противоречию: ребра, которые мы были вынуждены выбрать, образуют два несвязных цикла, а не один, существование которого мы предполагали. Вывод: граф, изображенный на рис. 4.11, не является гамильтоновым.

Гамильтоновы графы применяются для моделирования многих практических задач. Основой всех таких задач служит классическая задача коммивояжера.

Коммивояжер должен совершить поездку по городам и вернутся обратно, побывав в каждом городе ровно один раз, сведя при этом затраты на передвижение к минимуму.

Графическая модель задачи коммивояжера состоит из гамильтонова графа, вершины которого изображают города, а ребра — связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для путешествия по соответствующей дороге, такие, как, например, расстояние между городами или время движения по дороге. Граф, каждое ребро которого оснащено весом, называется нагруженным. Для решения задачи нам необходимо найти гамильтонов цикл минимального общего веса.

К сожалению, эффективный алгоритм решения данной задачи пока не известен. Для сложных сетей число гамильтоновых циклов, которые необходимо просмотреть для выделения минимального, непомерно огромно. Однако существуют алгоритмы поиска субоптимального решения. Субоптимальное решение необязательно даст цикл минимального общего веса, но найденный цикл будет, как правило, значительно меньшего веса, чем большинство произвольных гамильтоновых циклов! Один из таких алгоритмов мы сейчас, и изучим.

Алгоритм ближайшего соседа

Этот алгоритм выдает субоптимальное решение задачи коммивояжера, генерируя гамильтоновы циклы в нагруженном графе с множеством вершин V. Цикл, полученный в результате работы алгоритма, будет совпадать с конечным значением переменной маршрут, а его общая длина — конечное значение переменной w.

Пример 6.Примените алгоритм ближайшего соседа к графу, изображенному на рис. 4.12. За исходную вершину возьмите вершину D.

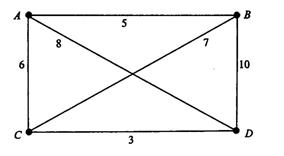
Рис. 4.12.

Решение.Смотри табл.4.2.

Таблица 4.2

	и	маршрут	w	v’
Исходные значения	—	D		D
	С	DC		С
	А	DCA		А
	В	DCAB		В
Последний проход	В	DCABD		В

В результате работы алгоритма был найден гамильтонов цикл DCABD общего веса 24. Делая полный перебор всех циклов в этом маленьком графе, можно обнаружить еще два других гамильтоновых цикла: ABCDA общего веса 23 и ACBDA общего веса 31. В полном графе с двадцатью вершинами существует приблизительно 6.1*10¹⁶ гамильтоновых циклов, перечисление которых требует чрезвычайно много машинной памяти и времени.

Деревья

Есть класс графов, называемых деревьями, которые особенно интенсивно используются в вычислительных приложениях. Граф G = (V, Е) называется деревом, если он связен и ацикличен (т.е. не содержит циклов).

Граф называется связным, если для любых его двух вершин существует маршрут, соединяющий эти вершины. Связный подграф, не являющийся собственным подграфом никакого другого подграфа исходного графа, называется компонентой связности графа.

Деревья являются в некотором смысле простейшим классом графов. Для них выполняются многие свойства, которые не выполняются для графов в общем случае. Деревья являются своего рода носителями связности.

Неориентированное дерево – это связный неориентированный граф без циклов, а следовательно, без петель и кратных ребер. Несвязный (неориентированный) граф без циклов называется лесом. Связные компоненты леса являются деревьями. Любая часть дерева или леса также не имеет циклов, т. е. является деревом или лесом. В качестве примера рассмотрим диаграммы всевозможных деревьев с четырьмя вершинами и леса (рис 4.13.).

Дерево с корнем или корневое дерево получается, если в дереве (связном ациклическом неориентированном графе) выделить одну из вершин, назвав ее корнем. Графически корневое дерево можно изобразить так, как это сделано на рис. 4.13. В).

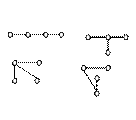
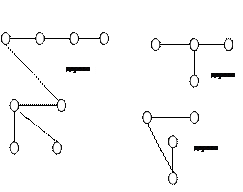
А) Б) В)

Рис. 4.13. А) Деревья; Б) Лес; В) Корневое дерево.

Таким образом, деревом называется связный неорграф, не содержащий циклов. Любой неорграф без циклов называется ациклическим графом или лесом. Таким образом, компонентами связности любого леса являются деревья.

Пусть G = (V, Е) — граф с п вершинами и т ребрами. Можно сформулировать несколько необходимых и достаточных условий, при которых G является деревом:

• Любая пара вершин в G соединена единственным путем.

• G связен и т = п — 1.

• G связен, а удаление хотя бы одного его ребра нарушает связность графа.

• G ацикличен, но если добавить хотя бы одно ребро, то в G появится цикл.

Эквивалентность большинства из этих условий устанавливается без особого труда. Наиболее сложно разобраться со вторым из них. В следующем примере мы докажем, что дерево с п вершинами имеет ровно (п — 1) ребро.

Пример 7.Докажите с помощью индукции по числу вершин, что для дерева Теп вершинами и т ребрами выполнено соотношение: т = п - 1.

Решение.Поскольку дерево с единственной вершиной вообще не содержит ребер, то доказываемое утверждение справедливо при п = 1.

Рассмотрим дерево Т с n вершинами (и т ребрами), где п > 1 и предположим, что любое дерево с k < п вершинами имеет ровно k - 1 ребро.

Удалим ребро из Т. По третьему свойству дерево Т после этой процедуры превратится в несвязный граф. Получится ровно две компоненты связности, ни одна из которых не имеет циклов (в противном случае исходный граф Т тоже содержал бы циклы и не могбы быть деревом). Таким образом, полученные компоненты связности — тоже деревья.

Обозначим новые деревья через T₁ и T₂. Пусть п₁количество вершин у дерева T₁, а п₂ - у Т₂. Поскольку п₁ + п₂= n то п₁< п и п₂ < п.

По предположению индукции дерево T₁имеет n₁ — 1 ребро, а Т₂ — п₂ – 1. Следовательно, исходное дерево Т насчитывало (с учетом одного удаленного) (п₁ - 1) + (п₂- 1) + 1 = п - 1 ребро, что и требовалось доказать.

Несложно доказать, что в любом связном графе найдется подграф, являющийся деревом. Подграф в G, являющийся деревом и включающий в себя все вершины G, называется остовным деревом. Остовное дерево в графе G строится просто: выбираем произвольное его ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла. Благодаря примеру 7.7, мы знаем, что для построения остовного дерева в графе из п вершин необходимо выбрать ровно п — 1 ребро.

Пример 8.Найдите два разных остовных дерева в графе, изображенном на рис. 4.14.

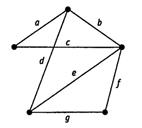
Рис. 4.14. Связный граф G

Решение.В этом графе существует несколько остовных деревьев. Одно из них получается последовательным выбором ребер: a, b, d и f. Другое — Ь, с, е и g. Названные деревья показаны на рис. 4.14. Процесс, описанный в примере 8, можно приспособить для решения задачи поиска кратчайшего соединения: Нужно построить железнодорожную сеть, связывающую некоторое число городов. Известна стоимость строительства отрезка путей между любой парой городов. Требуется найти сеть минимальной стоимости.

Ha языке теории графов нам нужно в нагруженном графе найти остовное дерево наименьшего общего веса. Такое дерево принято называть минимальным остовным деревом или, сокращенно, МОД. В отличие от задачи коммивояжера, здесь есть эффективный алгоритм, находящий действительно минимальное остовное дерево.

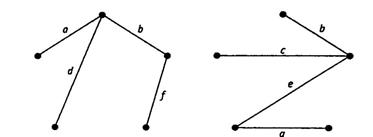
Рис. 4.15. Остовные деревья графа G

Пусть G = (V; E) – неориентированный граф (неорграф). Часть G' = (V';E') графа G является остовом или каркасом графа G, если V = V' и G' — лес, который на любой связной компоненте графа G образует дерево.

Таким образом, если G — связный граф,то остов G' является деревом, которое будем называть остовным деревом графа G. Понятие остова для орграфа G определяется как часть G графа G, для которой F(G') является остовом графа F(G). Аналогично вводится понятие остовного дерева для связного орграфа С.

Очевидно, что в каждом графе существует остов: Разрушая в каждой связной компоненте циклы, т. е. удаляя лишние ребра, получаем остов.

Из вышесказанного вытекает следующее:

1) Число ребер произвольного неорграфаG, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно т - п + с, где т — число ребер, п — число вершин, с — число компонент связности графа G.

Доказательство. Действительно, если i-я компонента связности С_i графа G содержит n_i вершин, то соответствующее дерево K_i остова содержит n_i - 1 ребро. Следовательно, для получения К_i из компоненты С_i нужно удалить m_i - (n_i - 1) ребер, где т_i — число ребер в C_i. Суммируя удаляемые ребра по всем компонентам связности и замечая, что 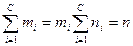получаем, что необходимо удалить 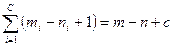ребер.

Число v(G) = т-п + с называется цикломатическим числом или циклическим рангом графа G. Число v*(G) = п - с называется коциклическим рангом или корангом. Такимобразом, v*(G) есть число ребер, входящих в любой остов rpacpa G, и v(G) + v*(G)=m.

Пример 9. В качестве остова графа G, изображенного на рис. 17, можно взять лес с ребрами 2, 3, 4 и 6, 7 (вообще говоря, остов определяется неоднозначно).

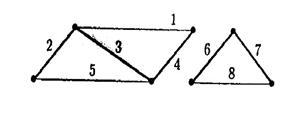
Рис. 4.16.

2) Неорграф G является лесом тогда и только тогда, когда v(G) = 0.

3)Неорграф G имеет единственный цикл тогда и только тогда, когда v(G) = 1.

Решение задачи нахождения остова минимального веса во взвешенном графе G = (V;E), заключается в следующем.

1. Строим граф Т_i, состоящий из множества вершин V и единственного ребра u_i, которое имеет минимальный вес.

2. Если граф T_i, уже построен и i < n – с, где п – количество вершин, с = c(G) – скомпонента связности, то строим граф Т_i+1, добавляя к множеству ребер графа Т_i ребро u_i+1, имеющее минимальный вес среди ребер, не входящих в Т_i и не составляющих циклов с ребрами из T_i.

Приведенный алгоритм, в частности, позволяет находить, остов в невзвешенном графе, положив w(u_i) = 1 для всех ребер u_i Є R.

Пример 10. На рис. 4.17 показан остов минимального веса взвешенного графа. Вес остова равен 9

.

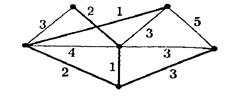
Рис. 4.17.