Формулы бернулли и Пуассона
АУДИТОРНАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА №3
1.Формула Бернулли
Пусть проводится сложный эксперимент, состоящий из 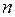 одинаковых независимых испытаний, причем в каждом испытании наблюдают за появлением события
одинаковых независимых испытаний, причем в каждом испытании наблюдают за появлением события 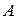 — успеха, или появлением противоположного события
— успеха, или появлением противоположного события 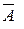 — неуспеха.
— неуспеха.
Вероятность успеха во всех опытах одинакова и равна 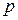 , т.е.
, т.е. 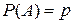 . Вероятность неуспеха
. Вероятность неуспеха 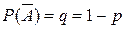 . В этом случае говорят, что испытания проводятся по схеме Бернулли.
. В этом случае говорят, что испытания проводятся по схеме Бернулли.
При вычислении вероятностей событий в эксперименте, проходящем по схеме Бернулли, справедливы следующие формулы:
1. Вероятность  появления успеха
появления успеха 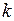 раз в серии из
раз в серии из 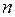 испытаний определяется по формуле, называемой формулой Бернулли:
испытаний определяется по формуле, называемой формулой Бернулли:
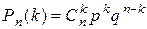 . (1.1)
. (1.1)
2. Вероятность 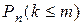 того, что событие
того, что событие 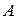 появится в
появится в 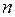 испытаниях не более
испытаниях не более 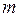 раз, вычисляется по формуле:
раз, вычисляется по формуле:
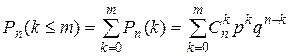 . (1.2)
. (1.2)
3. Вероятность появления события 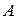 хотя бы один раз при
хотя бы один раз при 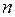 опытах определяется из соотношения
опытах определяется из соотношения
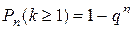 . (1.3)
. (1.3)
4. Количество 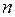 опытов, которые нужно произвести для того, чтобы с вероятностью не меньшей
опытов, которые нужно произвести для того, чтобы с вероятностью не меньшей 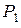 можно было утверждать, что событие
можно было утверждать, что событие 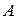 произойдет, по крайней мере, один раз, находится по формуле
произойдет, по крайней мере, один раз, находится по формуле
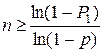 . (1.4)
. (1.4)
Задача 1.1. Три монеты одновременно подбрасываются 3 раза. Какова вероятность, что только в одном подбрасывании появятся три герба?
Решение: В этой задаче отдельное испытание Бернулли — это одновременное подбрасывание трех монет. Исход испытания — упорядоченная тройка гербов и решеток.
Пусть событие 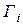 — выпадение герба у
— выпадение герба у 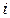 – той монеты при одном бросании
– той монеты при одном бросании 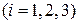 . Успех
. Успех 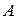 — появление трех гербов. Тогда событие
— появление трех гербов. Тогда событие 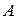 есть произведение трех независимых событий
есть произведение трех независимых событий 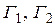 и
и 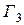 , т.е.
, т.е.
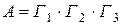 .
.
Поскольку 
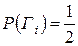 , а события
, а события 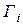
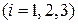 — независимы, то, по теореме умножения для независимых событий (2.10), вероятность
— независимы, то, по теореме умножения для независимых событий (2.10), вероятность 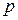 — успеха в отдельном испытании будет равна:
— успеха в отдельном испытании будет равна:
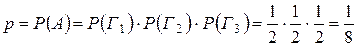 .
.
Тогда вероятность неуспеха определится из соотношения
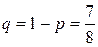 .
.
Число испытаний, проведенных по схеме Бернулли, 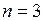 (подбрасывание трех монет производится трижды).
(подбрасывание трех монет производится трижды).
Интересующая нас вероятность — это вероятность появления ровно одного успеха в серии из трех испытаний. По формуле Бернулли (1.1), полагая 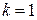 , вычислим требуемую вероятность.
, вычислим требуемую вероятность.
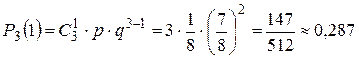 .
.
Задача 1.2. Играют два равносильных шахматиста. Что вероятнее выиграть: две партии из четырех или три из шести (ничейные исходы партий не учитываются)?
Решение: Независимыми испытаниями, проведенными по схеме Бернулли, в этой задаче являются отдельные сыгранные партии. Поскольку шахматисты равносильные, то вероятности выигрыша и проигрыша в каждой партии полагаем равными, т.е.
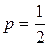 ,
, 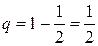 .
.
Вероятность выиграть две партии из четырех определяется по формуле Бернулли (1.1), в которой 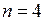 и
и 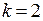 :
:
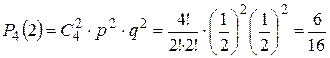 .
.
Вероятность выиграть три партии из шести, вычисленная по этой же формуле при 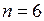 и
и 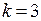 , равна:
, равна:
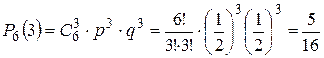 .
.
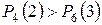 , поэтому вероятнее выиграть две партии из четырех.
, поэтому вероятнее выиграть две партии из четырех.
Задача 1.3. Завод изготавливает изделия, каждое из которых с вероятностью 0,01 имеет дефект. Каков должен быть объем 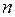 случайной выборки, чтобы вероятность встретить в ней хотя бы одно дефектное изделие, была не менее 0,95?
случайной выборки, чтобы вероятность встретить в ней хотя бы одно дефектное изделие, была не менее 0,95?
Решение: Пусть успех — событие 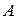 — изделие имеет дефект. По условию вероятность успеха
— изделие имеет дефект. По условию вероятность успеха  , тогда вероятность неуспеха
, тогда вероятность неуспеха 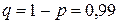 . Требуется найти минимальное количество испытаний
. Требуется найти минимальное количество испытаний 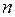 (объем выборки), чтобы с вероятностью, не меньшей
(объем выборки), чтобы с вероятностью, не меньшей 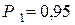 , событие
, событие 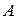 появилось хотя бы один раз.
появилось хотя бы один раз.
Используя формулу (1.4), получим
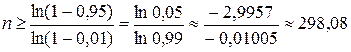 .
.
Следовательно, минимальный объем выборки 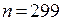 .
.
Решение задач 1.1 —1.3 в среде Mathcad показано на рис. 1.

Рис. 1
Задача 1.4. Независимо испытываются три прибора. Каждый при испытании выходит из строя с вероятностью 0,2. Найти вероятность того, что при испытании выйдет из строя хотя бы один прибор.
Решение: решение задачи по формуле (1.3), в которой 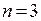 ,
, 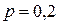 и, следовательно,
и, следовательно, 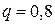 показано на рис. 2.
показано на рис. 2.
Задача 1.5. В систему массового обслуживания независимо друг от друга обращаются клиенты двух типов: обычные и с приоритетом в обслуживании. Вероятность поступления клиента с приоритетом равна 0,2. Найти вероятность того, что среди пяти обратившихся клиентов не более двух с приоритетом.
Решение: решение задачи по формуле (1.2), где 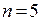 ,
, 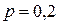 ,
, 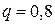 , а
, а 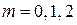 показано на рис. 2.
показано на рис. 2.

Рис. 2
